How to use the phase angle φ in the trigonometric function y=Asin(wx+φ)

What about φ in trigonometric function y Asinwx φ

1. Key point method:

When determining the φ value, consider the intersection of the function y=Asin(ωx φ) B and the x-axis. We need to find the abscissa of the point that initially intersects the x-axis, that is, let ωx φ=0. In this way, the value of φ can be determined. In order to choose the correct point to substitute into the analytical formula, we need to pay attention to which point in the "five-point method" the point belongs to. In the "five-point method", we choose the "first point", which refers to the point where the image intersects the x-axis when it rises. Therefore, ωx φ=0 at this time. Please note that your answer cannot exceed 112 words.

When the "maximum point" (that is, the "peak point" of the image)

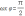
When the "minimum point" (that is, the "valley point" of the image)

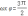
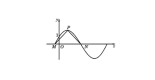
2. Substitution method:

The values ​​of A, ω and B can be determined by substituting known points into the equation or solving for the intersection of the image and the straight line. Pay attention to the intersection location.

Extended information:

Method of monotonicity of trigonometric function y=Asin (ωx φ):

1. We can understand the monotonicity of the function y=Asin (ωx φ) from the perspective of composite functions. The monotonicity of a composite function is determined by both the inner function and the outer function.

If the monotonicity of the inner function and the outer function is the same within a certain interval, the composite function is an increasing function. If the monotonicity of the inner function and the outer function is opposite within a certain interval, the composite function is a decreasing function. In short, both increase and decrease.

2. The image of function y=Asin (ωx φ) is obtained by the function y=sinx through stretching and translation transformation. The monotonicity of the function y=Asin (ωx φ) is also solved based on the function y=sinx.

The function y=Asin (ωx φ) can be seen as a composite of the function y=sint and the function t=ωx φ. The function t=ωx φ is a linear function, and its monotonicity is determined by the sign of ω.

So we only need to regard (ωx φ) as a whole and substitute it into the monotonic interval of y=sint.

For example, the monotonically increasing interval of function y=sint is [-(π/2) 2kπ, (π/2) 2kπ], then we can replace t as a whole with ωx φ, that is, -(π/2) 2kπ≤ ωxφ≤(π/2) 2kπ.

We only need to solve the inequality-(π/2) 2kπ≤(ωx φ)≤(π/2) 2kπ to get the monotonic interval of the function y=Asin(ωx φ).

3. In order to reduce the difficulty of analysis, we generally use the induction formula to change ω in the function y=Asin (ωx φ) to a positive number, so that we can ensure that the linear function t=ωx φ is on the real number set. increasing function.

We know from the properties of composite functions that if we want the monotonic increase (decrease) interval of the function y=Asin (ωx φ), we will bring the whole (ωx φ) into the monotonic increase (decrease) interval of the function y=sint, and then combine it The positive and negative of A, and finally solve the range of x. The solved x range is the monotonic interval of the function y=Asin (ωx φ).

Reference source: Encyclopedia - Trigonometric Functions

Slope formula of straight line

The formula for calculating the slope of a straight line: k=(y2-y1)/(x2-x1)

The tangent of the angle formed by a straight line and the X-axis on the right.

k=tanα=（y2-y1）/(x2-x1)or（y1-y2）/(x1-x2)

When the slope of the straight line L exists, for the linear function y=kx b (slope-intercept form), k is the slope of the function image (straight line).

Extended information

When the slope of straight line L does not exist, the slope-intercept formula y=kx b when k=0 y=b

When the slope of straight line L exists, the point slope formula y2—y1=k(X2—X1),

When the straight line L has a non-zero intercept on the two coordinate axes, there is an intercept formula X/a y/b=1

For any point on any function, its slope is equal to the angle between its tangent and the positive direction of the x-axis, that is, tanα

Slope calculation: ax by c=0, k=-a/b.

Line slope formula: k=(y2-y1)/(x2-x1)

The product of the slopes of two perpendicular intersecting straight lines is -1:k1*k2=-1.

When k>0, the greater the angle between the straight line and the x-axis, the greater the slope; when k

The above is the detailed content of How to use the phase angle φ in the trigonometric function y=Asin(wx+φ). For more information, please follow other related articles on the PHP Chinese website!