 Technology peripherals
Technology peripherals AI
AI General solution to unsupervised learning problems: a meta-algorithm-based framework
General solution to unsupervised learning problems: a meta-algorithm-based frameworkGeneral solution to unsupervised learning problems: a meta-algorithm-based framework
Researchers from Microsoft Research and Princeton University on November 13 proposed a general framework for designing efficient algorithms for unsupervised learning problems, such as a mixture of Gaussian distributions and subspace clustering.

#The framework proposed by the researchers uses a meta-algorithm to solve the noise problem, which uses the calculation method of the lower bound learning calculation formula. This framework is designed based on the recent work of Garg, Kayal, and Saha (FOCS'20), who proposed this framework for learning arithmetic formulas without any noise. A key element of the meta-algorithm is an efficient algorithm for solving a new problem called "robust vector space decomposition"
Research has shown that when some matrix has a sufficiently large minimum non-zero Meta-algorithms work well when dealing with singular values. "We conjecture that this condition holds for smoothed instances of our problem, and therefore our framework will yield efficient algorithms for these problems in smooth settings."
The study is titled "In Learning Arithmetic Formulas in the Presence of Noise: A General Framework and Applications to Unsupervised Learning, published on the arXiv preprint platform on November 13

Unsupervised learning involves discovering hidden patterns and structures in data without using any labels or direct human supervision.
Here, researchers consider data that has a good mathematical structure or is generated from a mathematically well-defined distribution. An example of the former is that data points can be grouped into meaningful clusters based on certain similarity patterns, and the goal is to find the underlying clusters. An example of the latter is mixture modeling, which assumes that data are generated by a mixture of succinctly described probability distributions (e.g. Gaussian distributions), and the goal is to learn the parameters of these distributions from samples.
A common framework for solving many unsupervised learning problems is the moment method, which exploits the statistical moments of the data to infer the underlying structure or underlying parameters of the model. For many unsupervised learning problem scenarios, where the underlying data has some nice mathematical structure, the moments of the data are well-defined functions of the parameters. Heuristic arguments suggest that the opposite should generally hold, i.e. the parameters of a structure/distribution are usually uniquely determined by some low-order moments of the data. In this general direction, the main challenge is to design algorithms to (approximately) recover the underlying parameters from (empirical) moments.
We also want the algorithm to be efficient, tolerant to noise (i.e., work well even if the moments are only known approximately, rather than exactly), and even tolerant of anomalies (i.e., Works well even if a few data points don't fit the underlying structure/distribution). But even the simplest problems in the field tend to be NP-hard, and remain so even in the absence of noise and outliers.
So one cannot actually expect an algorithm with provable worst-case guarantees. But one can hope that the algorithm is guaranteed to work generally well, i.e. for random problem instances, or more ideally for instances chosen in a smooth way. Therefore, many different algorithms have been designed for each such problem in unsupervised learning, with varying levels of efficiency, noise tolerance, outlier tolerance, and provable guarantees.
In this work, the researchers present a meta-algorithm applicable to many such unsupervised learning problems. The starting point of this study is the observation that many such problems boil down to the task of learning appropriate subclasses of arithmetic formulas.
The above is the detailed content of General solution to unsupervised learning problems: a meta-algorithm-based framework. For more information, please follow other related articles on the PHP Chinese website!
 Tesla's Robovan Was The Hidden Gem In 2024's Robotaxi TeaserApr 22, 2025 am 11:48 AM
Tesla's Robovan Was The Hidden Gem In 2024's Robotaxi TeaserApr 22, 2025 am 11:48 AMSince 2008, I've championed the shared-ride van—initially dubbed the "robotjitney," later the "vansit"—as the future of urban transportation. I foresee these vehicles as the 21st century's next-generation transit solution, surpas
 Sam's Club Bets On AI To Eliminate Receipt Checks And Enhance RetailApr 22, 2025 am 11:29 AM
Sam's Club Bets On AI To Eliminate Receipt Checks And Enhance RetailApr 22, 2025 am 11:29 AMRevolutionizing the Checkout Experience Sam's Club's innovative "Just Go" system builds on its existing AI-powered "Scan & Go" technology, allowing members to scan purchases via the Sam's Club app during their shopping trip.
 Nvidia's AI Omniverse Expands At GTC 2025Apr 22, 2025 am 11:28 AM
Nvidia's AI Omniverse Expands At GTC 2025Apr 22, 2025 am 11:28 AMNvidia's Enhanced Predictability and New Product Lineup at GTC 2025 Nvidia, a key player in AI infrastructure, is focusing on increased predictability for its clients. This involves consistent product delivery, meeting performance expectations, and
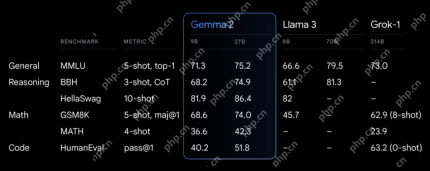 Exploring the Capabilities of Google's Gemma 2 ModelsApr 22, 2025 am 11:26 AM
Exploring the Capabilities of Google's Gemma 2 ModelsApr 22, 2025 am 11:26 AMGoogle's Gemma 2: A Powerful, Efficient Language Model Google's Gemma family of language models, celebrated for efficiency and performance, has expanded with the arrival of Gemma 2. This latest release comprises two models: a 27-billion parameter ver
 The Next Wave of GenAI: Perspectives with Dr. Kirk Borne - Analytics VidhyaApr 22, 2025 am 11:21 AM
The Next Wave of GenAI: Perspectives with Dr. Kirk Borne - Analytics VidhyaApr 22, 2025 am 11:21 AMThis Leading with Data episode features Dr. Kirk Borne, a leading data scientist, astrophysicist, and TEDx speaker. A renowned expert in big data, AI, and machine learning, Dr. Borne offers invaluable insights into the current state and future traje
 AI For Runners And Athletes: We're Making Excellent ProgressApr 22, 2025 am 11:12 AM
AI For Runners And Athletes: We're Making Excellent ProgressApr 22, 2025 am 11:12 AMThere were some very insightful perspectives in this speech—background information about engineering that showed us why artificial intelligence is so good at supporting people’s physical exercise. I will outline a core idea from each contributor’s perspective to demonstrate three design aspects that are an important part of our exploration of the application of artificial intelligence in sports. Edge devices and raw personal data This idea about artificial intelligence actually contains two components—one related to where we place large language models and the other is related to the differences between our human language and the language that our vital signs “express” when measured in real time. Alexander Amini knows a lot about running and tennis, but he still
 Jamie Engstrom On Technology, Talent And Transformation At CaterpillarApr 22, 2025 am 11:10 AM
Jamie Engstrom On Technology, Talent And Transformation At CaterpillarApr 22, 2025 am 11:10 AMCaterpillar's Chief Information Officer and Senior Vice President of IT, Jamie Engstrom, leads a global team of over 2,200 IT professionals across 28 countries. With 26 years at Caterpillar, including four and a half years in her current role, Engst
 New Google Photos Update Makes Any Photo Pop With Ultra HDR QualityApr 22, 2025 am 11:09 AM
New Google Photos Update Makes Any Photo Pop With Ultra HDR QualityApr 22, 2025 am 11:09 AMGoogle Photos' New Ultra HDR Tool: A Quick Guide Enhance your photos with Google Photos' new Ultra HDR tool, transforming standard images into vibrant, high-dynamic-range masterpieces. Ideal for social media, this tool boosts the impact of any photo,


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

WebStorm Mac version
Useful JavaScript development tools

Safe Exam Browser
Safe Exam Browser is a secure browser environment for taking online exams securely. This software turns any computer into a secure workstation. It controls access to any utility and prevents students from using unauthorized resources.

Notepad++7.3.1
Easy-to-use and free code editor




