Home >Technology peripherals >AI >Google: LLM can't find inference errors, but can correct it
Google: LLM can't find inference errors, but can correct it
- 王林forward
- 2023-11-27 14:39:201178browse
This year, large language models (LLM) have become the focus of much attention in the field of artificial intelligence. LLM has made significant progress in various natural language processing (NLP) tasks, especially in reasoning. However, LLM's performance on complex reasoning tasks still needs to be improved
Can LLM determine that there are errors in its own reasoning? A recent study jointly conducted by the University of Cambridge and Google Research found that LLM was unable to detect inference errors on its own, but was able to correct them using the backtracking method proposed in the study

- Paper address: https://arxiv.org/pdf/2311.08516.pdf
- Dataset address: https://github.com/WHGTyen/BIG-Bench-Mistake
This paper caused some controversy, and some people commented on this Raise objections. For example, on Hacker News, someone commented that the title of the paper was exaggerated and a bit clickbait. Others criticize that the method for correcting logical errors proposed in the paper is based on pattern matching rather than using logical methods. This method is prone to failure.
Huang et al. in the paper "Large language models" cannot self-correct reasoning yet" points out: Self-correction may be effective in improving the style and quality of model output, but there is little evidence that LLM has the ability to identify and correct its own reasoning and logical errors without external feedback. For example, both Reflexion and RCI use the correction result of the ground truth as a signal to stop the self-correction cycle.
The research team from the University of Cambridge and Google Research proposed a new idea: dividing the self-correction process into two stages: error discovery and output correction
- Error detection is a basic reasoning skill that has been widely studied and applied in the fields of philosophy, psychology and mathematics, and has given rise to concepts such as critical thinking, logical and mathematical fallacies. It is reasonable to assume that the ability to detect errors should also be an important requirement for LLM. However, our results show that state-of-the-art LLMs are currently unable to reliably detect errors.
- Output correction involves partial or complete modification of previously generated output. Self-correction means that the correction is done by the same model that generated the output. Although LLM does not have the ability to detect errors, this paper shows that if information about the error is provided (such as through a small supervised reward model), LLM can correct the output using a backtracking method.
The main contributions of this article include:
- Using the thinking chain prompt design method, any task can become a mistake Discovery mission. For this purpose, the researchers collected and released a CoT-type trajectory information data set BIG-Bench Mistake, which was generated by PaLM and marked the location of the first logical error. Researchers say BIG-Bench Mistake is the first dataset of its kind that is not limited to mathematical problems.
- To test the inference capabilities of current state-of-the-art LLMs, the researchers benchmarked them based on new datasets. It was found that it is difficult for the current SOTA LLM to detect errors, even if they are objective and clear errors. They speculate that LLM's inability to detect errors is the main reason why LLM cannot self-correct reasoning errors, but this aspect requires further research.
- This article proposes to use the backtracking method to correct the output and use the wrong position information to improve the performance on the original task. Research has shown that this method can correct an otherwise incorrect output with minimal impact on an otherwise correct output.
- This article explains the backtracking method as a form of "verbal reinforcement learning", which can achieve iterative improvement of CoT output without any weight updates. The researchers proposed that backtracking can be used by using a trained classifier as a reward model, and they also experimentally demonstrated the effectiveness of backtracking under different reward model accuracy.
BIG-Bench Mistake Dataset
BIG-Bench contains 2186 trajectory information sets using CoT style. Each trajectory was generated by PaLM 2-L-Unicorn and the location of the first logical error was annotated. Table 1 shows an example of a trajectory where the error occurs at step 4

These trajectories are from 5 tasks in the BIG-Bench dataset: Word Sorting, tracking shuffled objects, logical deduction, multi-step arithmetic, and the Dyck language.
To answer the questions of each task, they used the CoT prompt design method to call PaLM 2. In order to separate the CoT trajectory into clear steps, they used the method proposed in "React: Synergizing reasoning and acting in language models" to generate each step separately and use newlines as stop markers
When all trajectories are generated, in this dataset, when temperature = 0, the correctness of the answer is determined by an exact match
Benchmark results
On the new bug discovery dataset, the reported accuracies of GPT-4-Turbo, GPT-4 and GPT-3.5-Turbo are shown in Table 4
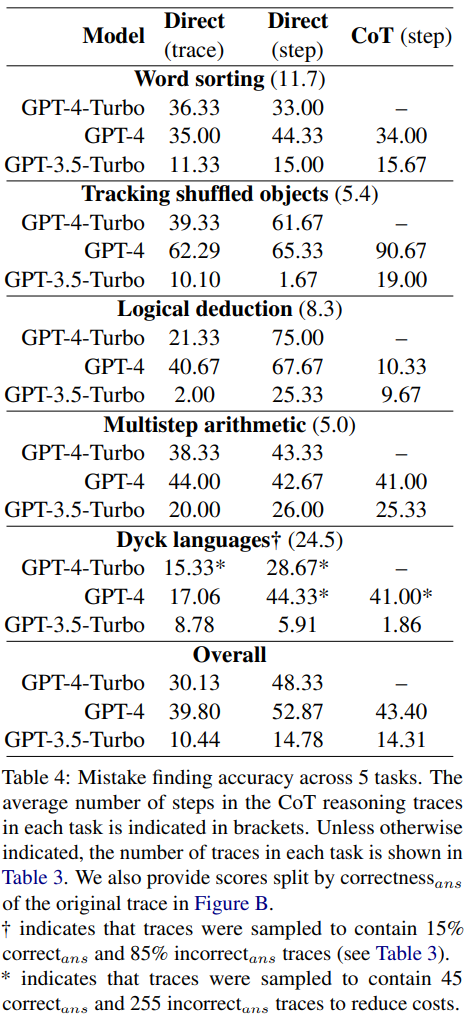
Each question has two possible answers: either correct or incorrect. If it is an error, the value N will indicate the step where the first error occurred
All models were entered with the same 3 prompts. They used three different prompt design methods:
- Direct track-level prompt design
- Direct step-level prompt design prompt design
- CoT step-level prompt design
The content that needs to be rewritten is: related discussion
The results show that all three models struggle to cope with this new error discovery dataset. GPT performs best, but it can only achieve an overall accuracy of 52.87 in direct step-level prompt design.
This illustrates the difficulty that current state-of-the-art LLMs have in finding errors, even in the simplest and clearest cases. In contrast, humans can find errors without specific expertise and with high consistency.
Researchers speculate that LLM’s inability to detect errors is the main reason why LLM cannot self-correct reasoning errors.
prompt Comparison of design methods
The researchers found that moving from a direct trajectory-level approach to a step-level approach Moving to the CoT method, the accuracy of the trajectory is significantly reduced without errors. Figure 1 shows this trade-off
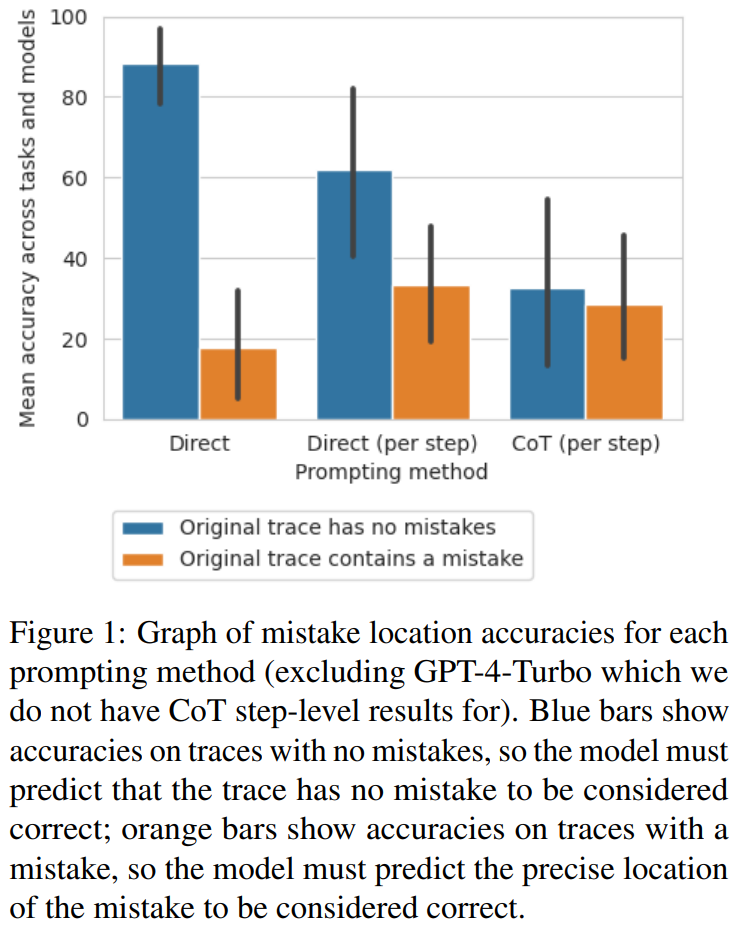
#The researchers believe that the reason for this may be the number of model outputs. All three methods require the generation of increasingly complex outputs: prompt design methods that directly generate trajectories require a single token, prompt design methods that directly generate steps require one token per step, and CoT step-level prompt design methods require each step Multiple sentences. If there is some probability of an error rate per build call, the more calls per trace, the greater the chance that the model will identify at least one error
Few-shot prompt design using error location as a proxy for correctness
The researchers explored whether these prompt design methods can reliably determine the correctness of a trajectory rather than the error location. .
They calculated the average F1 score, which is based on whether the model can correctly predict whether there are errors in the trajectory. If there is an error, the trajectory predicted by the model is considered to be the "wrong answer". Otherwise, the trajectory predicted by the model is considered the "correct answer"
Using correct_ans and incorrect_ans as positive labels, and weighted according to the number of occurrences of each label, the researchers calculated the average F1 scores, the results are shown in Table 5.
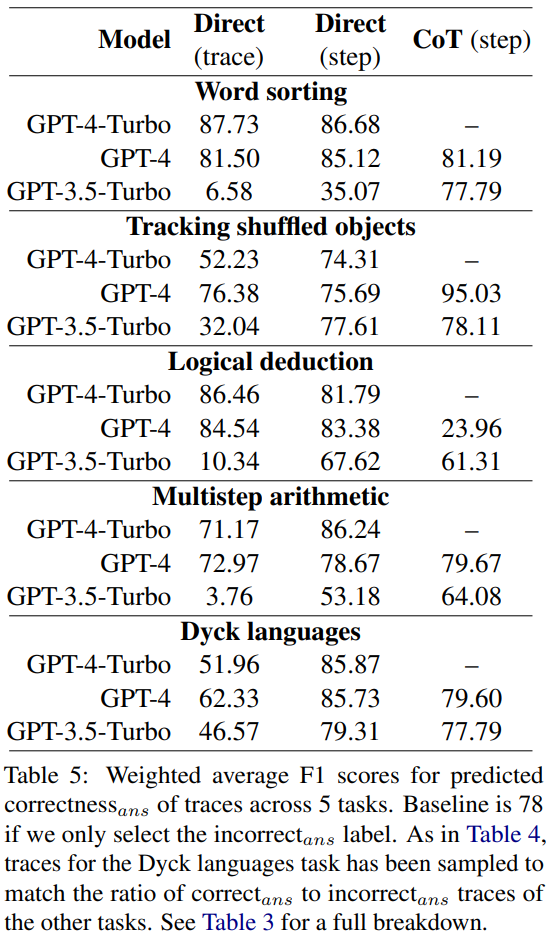
This weighted F1 score shows that looking for errors through the prompt is a poor strategy for determining the correctness of the final answer.
Backtrack
Huang et al. pointed out that LLM cannot self-correct logic errors without external feedback. However, in many real-world applications, there is often no external feedback available. In this study, the researchers adopted an alternative: using one on a small amount of data. Trained lightweight classifiers replace external feedback. Similar to reward models in traditional reinforcement learning, this classifier can detect any logical errors in CoT trajectories before feeding them back to the generator model to improve the output. If you want to maximize the improvement, you can do multiple iterations.
The researcher proposed a simple method to improve the output of the model by backtracking the location of logical errors
- The model first generates an initial CoT trajectory . In experiments, set temperature = 0.
- The reward model is then used to determine the location of the error in the trajectory.
- If there are no errors, move to the next track. If there are errors, prompt the model again to perform the same steps, but this time with temperature = 1, producing 8 outputs. The same prompt is used here along with a partial trace of all the steps before the erroneous step.
- In these 8 outputs, filter out options that are the same as the previous error. Then select the one with the highest logarithmic probability from the remaining outputs.
- Finally, replace the previous step with the new regenerated step, reset temperature = 0, and continue generating the remaining steps of the trajectory.
Compared with the previous self-correction method, this backtracking method has many advantages:
- New backtracking Methods require no prior knowledge of the answer. Instead, it relies on information about logical errors (such as that from a trained reward model), which can be determined step-by-step using the reward model. Logical errors may or may not appear in the correct_ans trajectory.
- The backtracking method does not rely on any specific prompt text or wording, thus reducing related preferences.
- Compared with methods that require regeneration of the entire trajectory, the backtracking method can reduce computational costs by reusing known logically correct steps.
- Backtracking methods can directly improve the quality of intermediate steps, which may be useful in scenarios where correct steps are required (such as generating solutions to mathematical problems), while also improving interpretability .
The researchers conducted experiments using the BIG-Bench Mistake dataset to explore whether the backtracking method can help LLM correct logic errors. Please see Table 6 for the experimental results
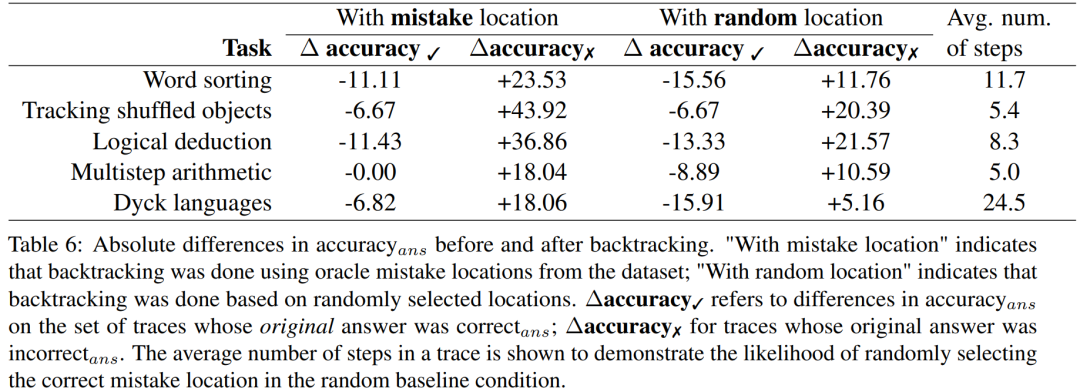
Δaccuracy✓ refers to the trajectory set when the original answer is correct_ans The difference between accuracy_ans.
For the results of incorrect answer trajectories, the accuracy needs to be recalculated
These score results show that the benefit of correcting the incorrect_ans trajectory is greater than changing the original correct the answer to the damage caused. Furthermore, although random benchmarks also gain improvements, their gains are significantly smaller than when using true error locations. Note that in randomized benchmarks, performance gains are more likely to occur on tasks involving fewer steps, since it is more likely to find the location of the true error.
To explore which accuracy level reward model is needed when good labels are not available, they experimented with using backtracking through a simulated reward model; the design of this simulated reward model The goal is to produce labels with different accuracy levels. They use accuracy_RM to represent the accuracy of the simulation reward model at a specified error location.
When the accuracy_RM of a given reward model is X%, use the error location from BIG-Bench Mistake X% of the time. For the remaining (100 − X)%, an error location is randomly sampled. To simulate the behavior of a typical classifier, error locations are sampled in a way that matches the distribution of the data set. The researchers also found ways to ensure that the wrong location of the sample did not match the correct location. The results are shown in Figure 2.
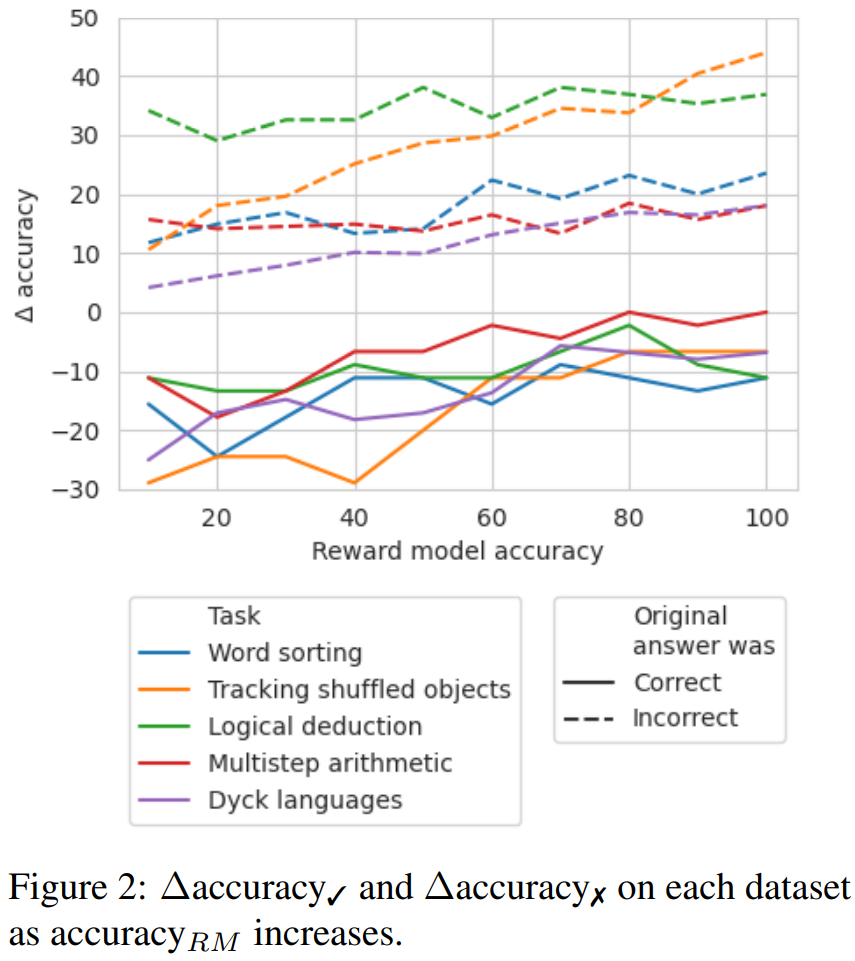
It can be observed that when the loss rate reaches 65%, the Δ accuracy begins to stabilize. In fact, for most tasks, Δaccuracy ✓ already exceeds Δaccuracy ✗ when accuracy_RM is about 60-70%. This shows that while higher accuracy leads to better results, backtracking still works even without the gold standard error location label
The above is the detailed content of Google: LLM can't find inference errors, but can correct it. For more information, please follow other related articles on the PHP Chinese website!
Related articles
See more- php '7-Day Devil Training Camp' free live course registration notice! ! ! ! ! !
- What is the css box model?
- What is the OSI model
- Programmers are in danger! It is said that OpenAI recruits outsourcing troops globally and trains ChatGPT code farmers step by step
- Yunshenchen and Shengteng CANN work together to open a ROS four-legged robot dog development training camp

