Home >Technology peripherals >AI >Terence Tao approaches another 60-year geometry problem! A new breakthrough has been made in the problem of periodic close paving
Terence Tao approaches another 60-year geometry problem! A new breakthrough has been made in the problem of periodic close paving
- PHPzforward
- 2023-10-14 14:17:071099browse
Tao Zhexuan made a new breakthrough in studying the periodic dense paving problem
On September 18, Tao Zhexuan and Rachel Greenfeld published the preprinted paper "Translational Single Mingling Pavement" "Undecidability of translational monotilings" was uploaded to arXiv.

Paper address: https://arxiv.org/abs/2309.09504
This paper The main conclusion is that if the dimensions of the grid are unbounded, then the problem of determining whether a finite subset of the grid can tile a periodic subset of the grid is undecidable
Be aware that this problem is decidable in dimension 1 and dimension 2.
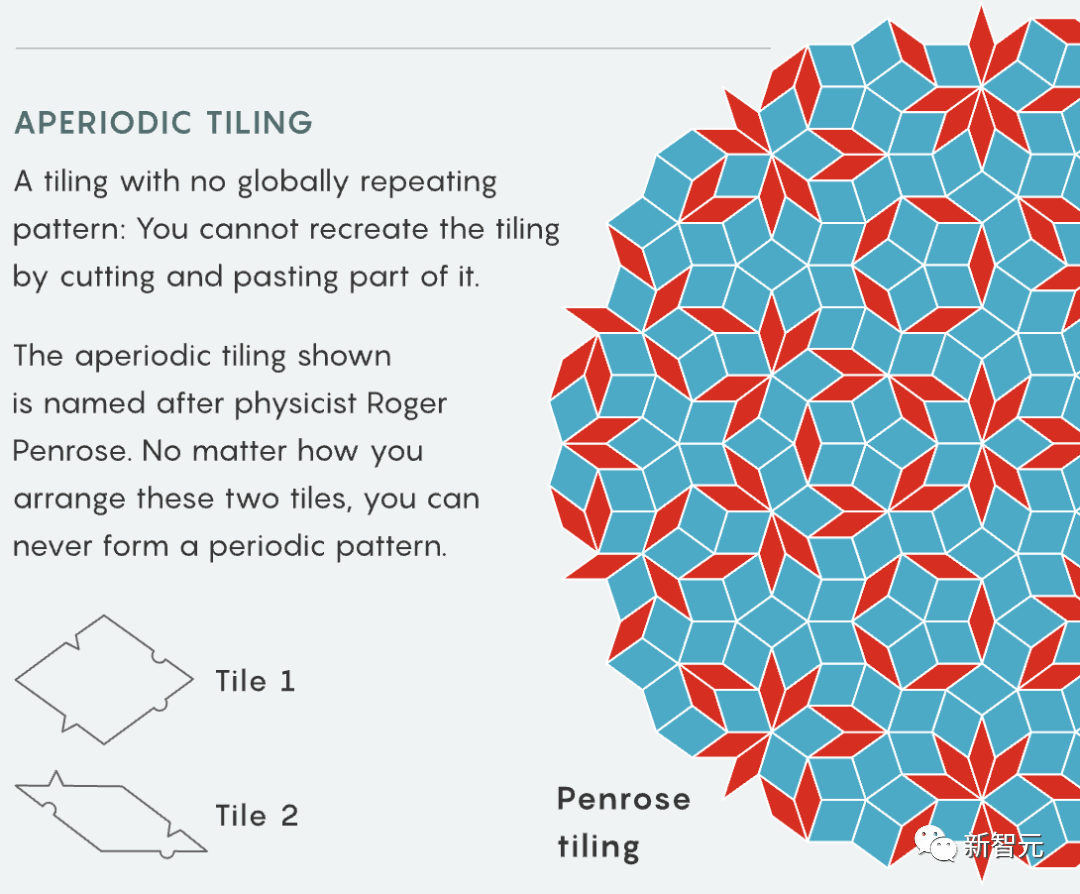
Tao Zhexuan said that it is a bit strange that most of the components demonstrated in the article are similar to popular games——
There are dense analogues of dominoes, Sudoku, the computer game "Tetris", and even the children's game "Fizz buzz"
Why study one Why do math problems involve so many games? Terence Tao also cannot explain

The undecidability of translational single dense tiling
This paper, It is a sequel to the two's previous paper. Link Periodic Tiles Problem
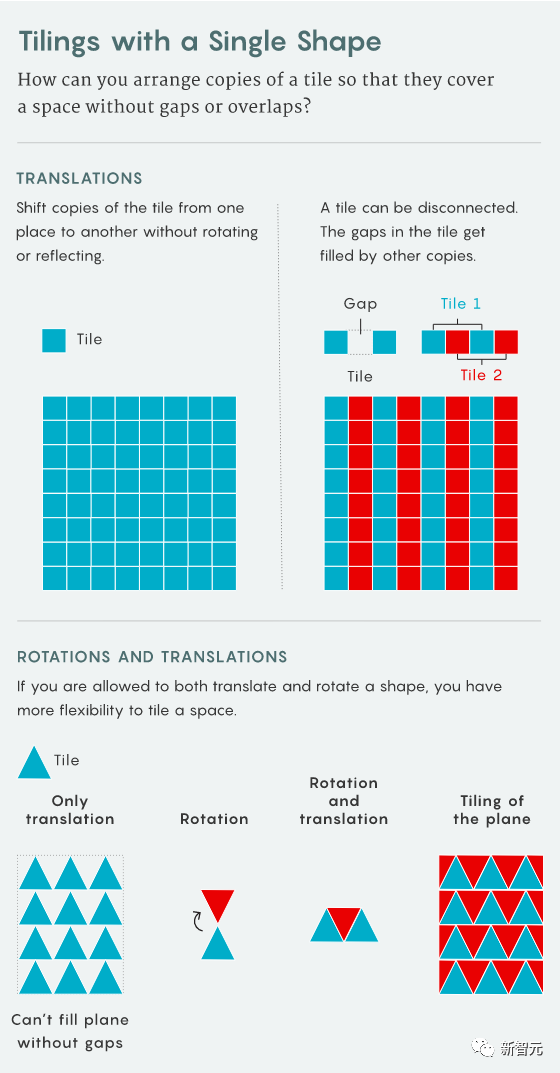
In the last paper, they constructed a high-dimensional grid The translation of the single dense pavement
The translation of the single dense pavement 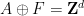
(therefore the single dense pavement 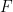 is a finite set), which is non-periodic (There is no way to "fix" this tile into a periodic tile
is a finite set), which is non-periodic (There is no way to "fix" this tile into a periodic tile  , where
, where 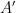 is now relative to the finite index subgroup
is now relative to the finite index subgroup  is periodic).
is periodic).

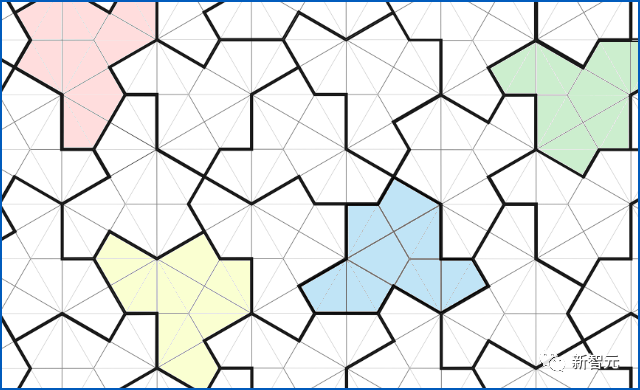
This fact negates the hypothesis of Stein, Grunbaum-Shephard and Lagarias-Wang about the non-existence of aperiodic closely packed monomers
("Hat single dense paving" is a recently discovered non-periodic equidistant single dense paving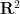 . In this kind of single dense paving, it is allowed to use Rotation, reflection and translation, or the newer "ghost monolith". These monoliths are similar to hat monoliths, except no reflection is required).
. In this kind of single dense paving, it is allowed to use Rotation, reflection and translation, or the newer "ghost monolith". These monoliths are similar to hat monoliths, except no reflection is required).
One of the reasons why Terence Tao and Rachel Greenfeld inspired this conjecture is the observation of mathematician Hao Wang

He found that if the periodic tessellation conjecture is true, then the translational tessellation problem is algorithmically decidable——
There is a Turing machine, for  , when given a dimension
, when given a dimension 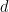 and a finite subset
and a finite subset 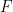 At this time, you can determine within a limited time whether
At this time, you can determine within a limited time whether 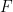 can be densely paved
can be densely paved 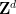 .
.
This is because if there is a periodic tiling, it can be found through a computer search
If there is no tiling at all, Then it can be known from the compactness theorem that there are some limited  subsets that cannot be covered by
subsets that cannot be covered by 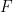 disjoint translations. This can also be done by computer Search to discover.
disjoint translations. This can also be done by computer Search to discover.
The periodic tessellation conjecture asserts that these are the only two possible situations, thus giving decidability.

On the other hand, Wang’s point of view is immutable: the failure of the periodic tessellation conjecture does not automatically mean that the translational tessellation conjecture The undecidability of the problem, since it does not rule out the existence of other algorithms to determine the tiling that do not depend on the existence of periodic tiling
(e.g. even if With the newly discovered hat and ghost tiling, it is still an open question whether the isometric single tiling problem of polygons with rational coefficients in 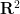 is decidable, whether or not it has reflections.
is decidable, whether or not it has reflections.
The main results of this article address this issue (with a caveat):

What needs to be rewritten is: Theorem 1
does not exist any algorithm, for 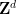 , given a dimension
, given a dimension  , a periodic subset
, a periodic subset 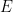 , and a finite subset
, and a finite subset 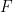 , which can determine whether there is a translational tiling in a limited time
, which can determine whether there is a translational tiling in a limited time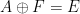 .
.
It should be noted that the periodic subset 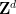 of
of  must be used instead of all
must be used instead of all  ; This is largely due to technical limitations of this approach and is likely to be eliminated with additional effort and creativity.
; This is largely due to technical limitations of this approach and is likely to be eliminated with additional effort and creativity.
In addition, Terence Tao and Rachel Greenfeld also noticed that when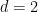 , the periodic pavement conjecture was established by Bhattacharya, so in
, the periodic pavement conjecture was established by Bhattacharya, so in In this case, the problem can be determined.
In this case, the problem can be determined.
For any fixed value of 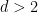 , it is still open whether the tiling problem is decidable (note that in the above results, the dimension
, it is still open whether the tiling problem is decidable (note that in the above results, the dimension 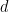 is not fixed, but part of the input).
is not fixed, but part of the input).
This theorem also implies that due to the well-known connection between algorithmic undecidability and logical undecidability (also known as logical independence) It turns out that there exists a (in principle unambiguously describable) periodic subset of the dimensions  ,
, 
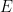 ,# The finite subset
,# The finite subset 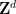 of
of  ##, so that
##, so that 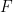 can be passed through translational tiling
can be passed through translational tiling 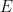 cannot be used in ZFC set theory Confirm or falsify (assuming of course that the theory is consistent).
cannot be used in ZFC set theory Confirm or falsify (assuming of course that the theory is consistent).
As a result of this approach, we can also use the "almost two-dimensional" group  instead of ## here #, where
instead of ## here #, where 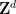 is a finite abelian group (now part of the input, instead of dimension
is a finite abelian group (now part of the input, instead of dimension 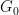 ).
). 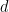
A common way to prove that a problem is undecidable is to "encode" other problems that are known to be undecidable into the original problem, so that any algorithm that determines the original problem can also determine it. Embedded Question
Therefore, we encode Wang’s dense paving problem as a single dense paving problem The second question is about the Wang’s secret shop problem Given a limited Wang’s secret shop set Berger once famously concluded that this question cannot be determined The content that needs to be rewritten is: Berger, Robert, Converting this problem into a high-dimensional translational single dense tiling problem requires solving some intermediate problems First, we can easily embed the Wang's secret shop problem into a similar problem, which we call the domino problem: Rewritten as follows: Domino problem is problem 3 Given a level (or vertical) finite set of dominoes In fact, we only need to insert each Wang's tile as a separate "point" and define the domino set In the next steps we will combine the domino problem with the Sudoku problem: Question 4 (Sudoku problem) Given column width Embedding the Sudoku problem into the single dense pavement problem is based on the modification method proposed in previous papers These papers also proposed Different versions of Sudoku problems, and created a method called "Tab Language" that can transform various problems (including Sudoku problems) into a single Tile Problem To encode a domino problem as a Sudoku problem, we need to get a domino function (which obeys the same rules as certain domino sets This approach is not immediately obvious, but Tao and Rachel Greenfeld adapted some of Aanderaa and Lewis's ideas with the help of Emmanuel Jeandel, and certain hierarchies were used to encode one question into another. Here we explain the hierarchical structure Then, use the formula is two different large prime numbers (for example, you can take ,and , the first component of (1) looks like this: looks like this:  :
: 
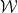 (unit (square, each edge assigned a certain color from a limited palette), is it possible to tessellate a plane using a standard grid
(unit (square, each edge assigned a certain color from a limited palette), is it possible to tessellate a plane using a standard grid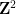 by translation so that adjacent tiles are in common Have the same color on the edges?
by translation so that adjacent tiles are in common Have the same color on the edges? 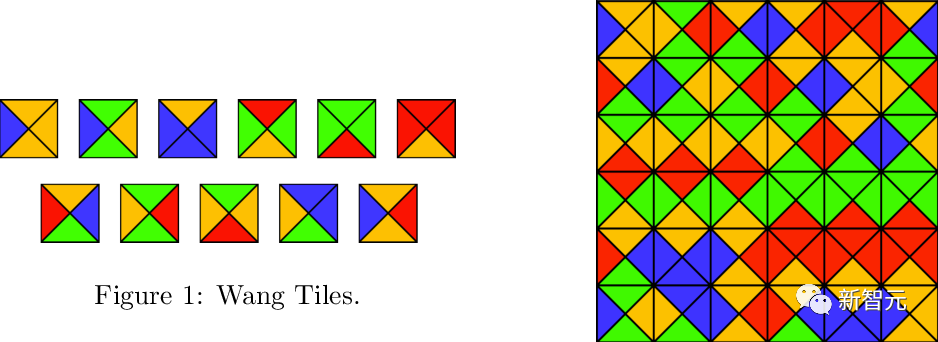


 or
or  , which are a pair of adjacent unit squares, each unit square is represented by a finite set ## To decorate it with an element point in
, which are a pair of adjacent unit squares, each unit square is represented by a finite set ## To decorate it with an element point in 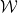 #, is it possible to assign a point to each unit square in the standard lattice tiling
#, is it possible to assign a point to each unit square in the standard lattice tiling 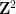 , so that each pair in this tiling Can horizontal (or vertical) squares use dominoes from
, so that each pair in this tiling Can horizontal (or vertical) squares use dominoes from 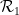 or
or 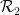 ?
? 
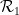 ,
,  are pairs of Wang's dense tiles that are adjacent horizontally or vertically and have the same edge color.
are pairs of Wang's dense tiles that are adjacent horizontally or vertically and have the same edge color. 
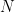 , set of numbers
, set of numbers 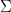 , set of functions
, set of functions 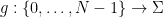
 , and "initial conditions"
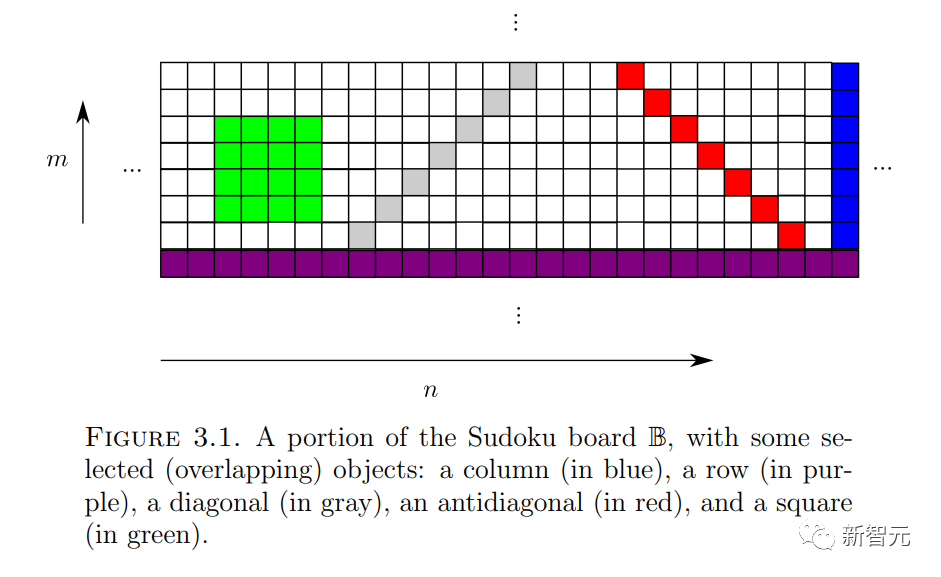
, and "initial conditions" 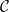 (I won’t go into details here), is it possible to assign a number to each cell
(I won’t go into details here), is it possible to assign a number to each cell 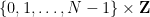 in the "Sudoku board"
in the "Sudoku board"  ## so that for any slope
## so that for any slope 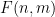 and intercept
and intercept 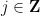 , the number
, the number 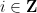 # along the
# along the 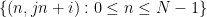 line ## is located in
line ## is located in 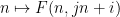 (and
(and 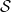 is subject to the initial condition
is subject to the initial condition 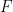 )?
)? 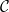
 The most novel part of this paper is to prove that the domino problem can indeed be embedded in a Sudoku problem.
The most novel part of this paper is to prove that the domino problem can indeed be embedded in a Sudoku problem. 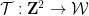 associated domino constraints) and use it to construct the Sudoku function
associated domino constraints) and use it to construct the Sudoku function 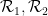 (which obeys some Sudoku constraints associated with the domino set); conversely, each obeys the Sudoku puzzle rules Sudoku functions must be generated from domino functions in some way.
(which obeys some Sudoku constraints associated with the domino set); conversely, each obeys the Sudoku puzzle rules Sudoku functions must be generated from domino functions in some way. 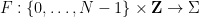

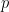 (due to the two-dimensional nature of the domino problem, two different primes need to be used).
(due to the two-dimensional nature of the domino problem, two different primes need to be used). 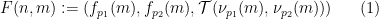 to construct the Sudoku function
to construct the Sudoku function 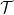 , which There will be some kind of embedding.
, which There will be some kind of embedding. 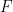 where
where 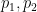 ,
, 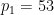 ),
), 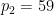 represents the number of times
represents the number of times 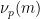 is divided by
is divided by 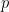 , and
, and 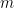
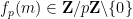 expansion of
expansion of 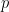 :
: 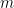
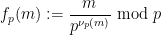 (
(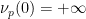 ).
).  In the case of
In the case of 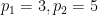
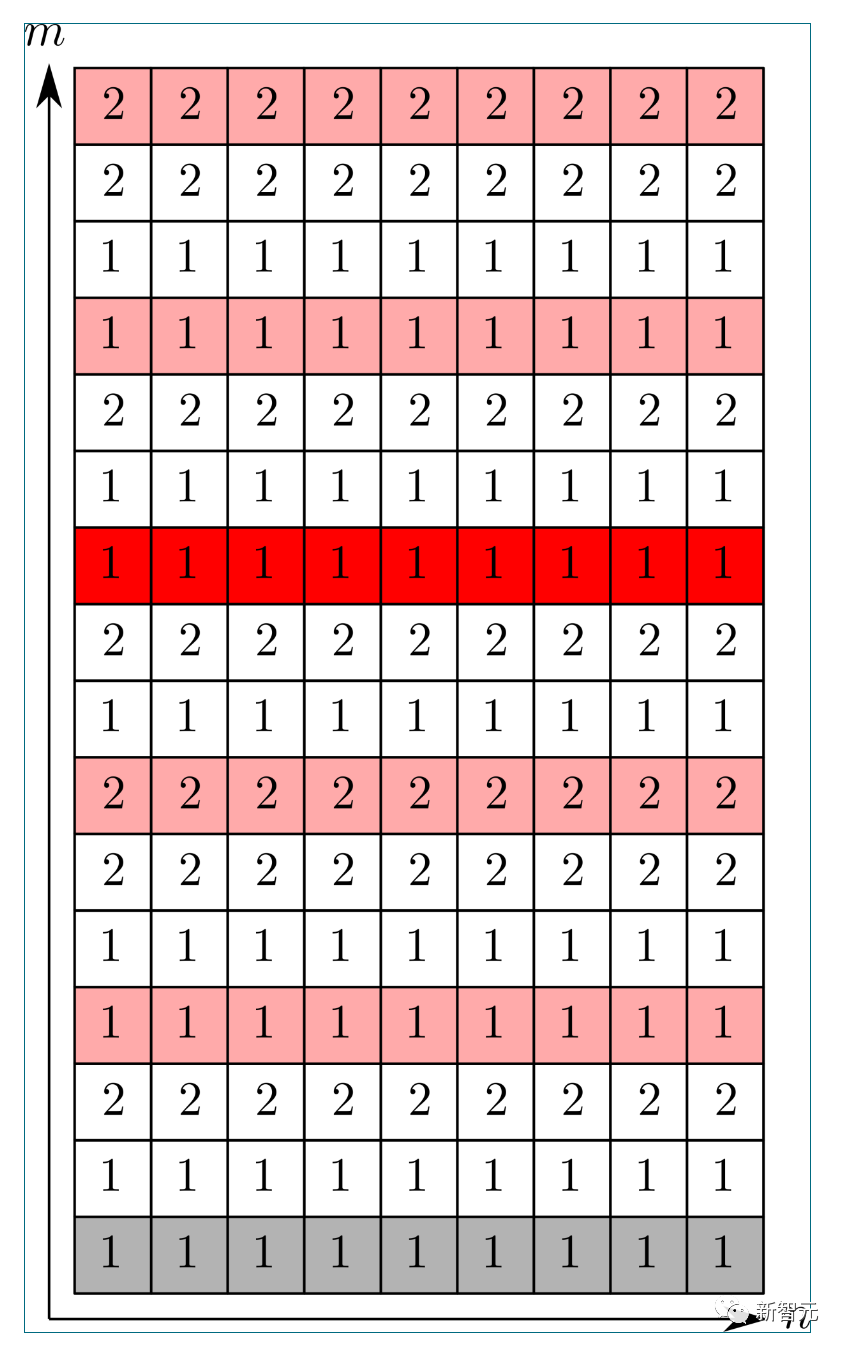 A typical example of the final component
A typical example of the final component 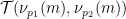
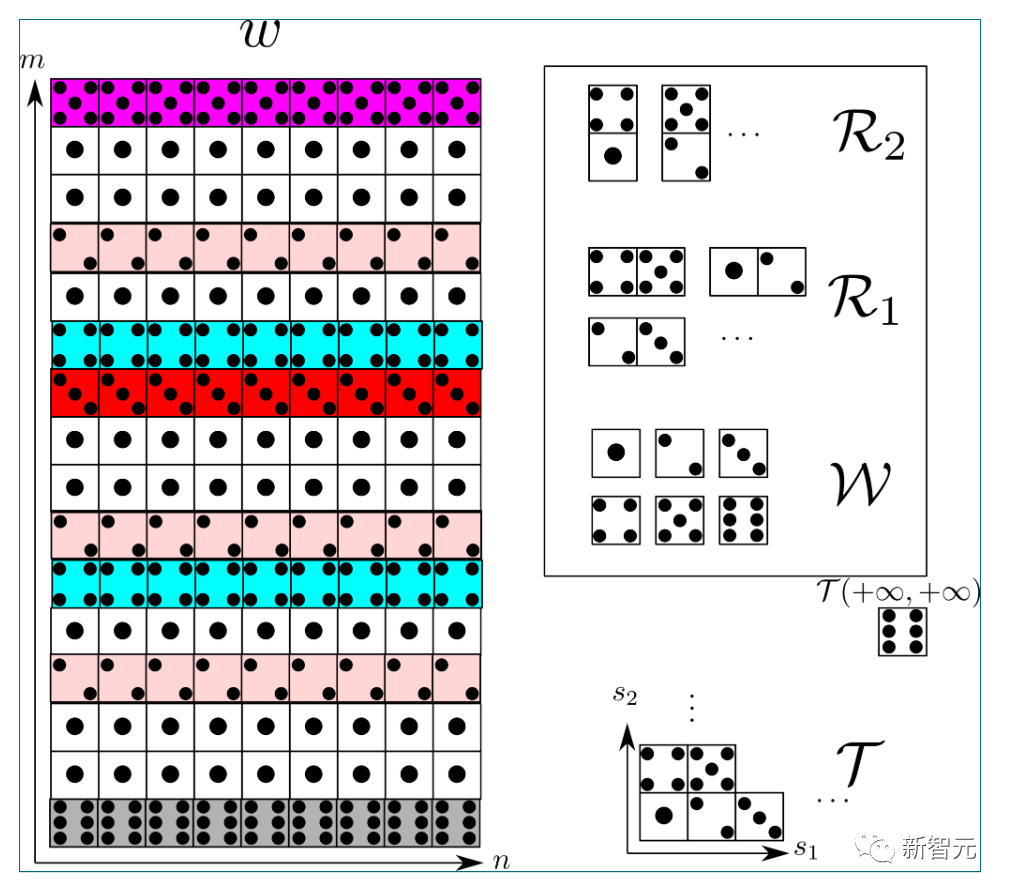 Interesting Yes, I don’t know why, but the decoration here basically follows the rules of the children’s game “Fizz Buzz”
Interesting Yes, I don’t know why, but the decoration here basically follows the rules of the children’s game “Fizz Buzz”
The above is the detailed content of Terence Tao approaches another 60-year geometry problem! A new breakthrough has been made in the problem of periodic close paving. For more information, please follow other related articles on the PHP Chinese website!
Related articles
See more- 4 tips for using the substitute function in Excel function learning
- Google solves the problem of storing and manipulating n-dimensional data with an open source software library
- GPT-4 has great mathematical ability! OpenAI's explosive research on 'Process Supervision” breaks through 78.2% of the problems and eliminates hallucinations
- World's first: Molecular Heart's new AI algorithm to overcome the problems of protein side chain prediction and sequence design

