Reverse thinking: MetaMath new mathematical reasoning language model trains large models

Complex mathematical reasoning is an important indicator for evaluating the reasoning ability of large language models. Currently, the commonly used mathematical reasoning data sets have limited sample sizes and insufficient problem diversity, resulting in the phenomenon of "reversal curse" in large language models, that is, a A language model trained on "A is B" cannot be generalized to "B is A" [1]. The specific form of this phenomenon in mathematical reasoning tasks is: given a mathematical problem, the language model is good at using forward reasoning to solve the problem but lacks the ability to solve the problem with reverse reasoning. Reverse reasoning is very common in mathematical problems, as shown in the following 2 examples.

1. Classic problem - chickens and rabbits in the same cage

• Forward reasoning: There are 23 chickens and 12 rabbits in the cage , ask how many heads and how many feet are there in the cage?
• Reverse reasoning: There are several chickens and rabbits in the same cage. Counting from the top, there are 35 heads, and counting from the bottom, there are 94 legs. How many chickens and rabbits are there in the cage?

2. GSM8K Question

• Forward reasoning: James buys 5 packs of beef that are 4 pounds each. The price of beef is $5.50 per pound. How much did he pay?
• Converse reasoning: James buys x packs of beef that are 4 pounds each. The price of beef is $5.50 per pound. . How much did he pay? If we know the answer to the above question is 110, what is the value of unknown variable x?

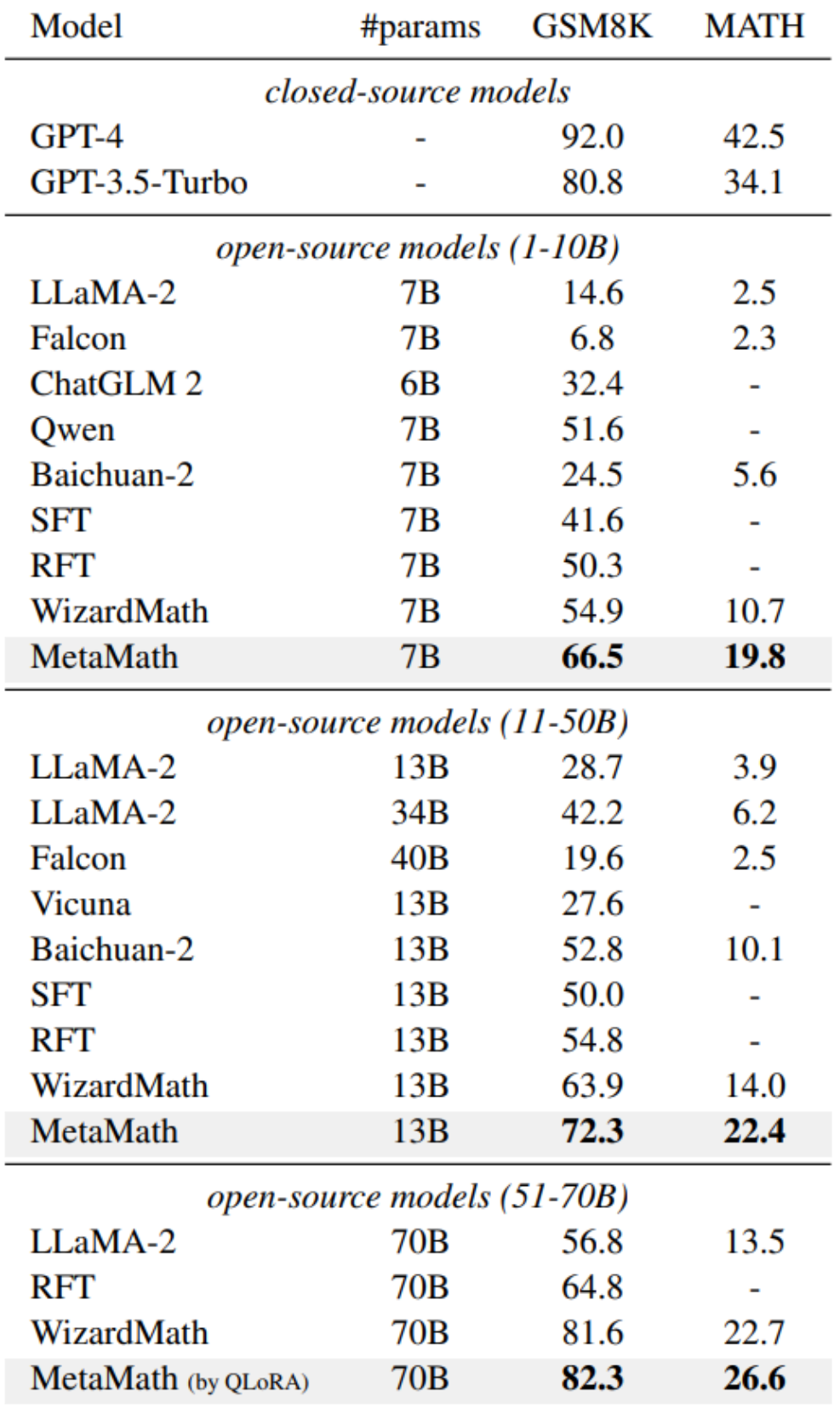
In order to improve the forward sum of the model For reverse reasoning capabilities, researchers from Cambridge, Hong Kong University of Science and Technology, and Huawei proposed the MetaMathQA data set based on two commonly used mathematical data sets (GSM8K and MATH): a mathematical reasoning data set with wide coverage and high quality. MetaMathQA consists of 395K forward-inverse mathematical question-answer pairs generated by a large language model. They fine-tuned LLaMA-2 on the MetaMathQA data set to obtain MetaMath, a large language model focusing on mathematical reasoning (forward and inverse), which reached SOTA on the mathematical reasoning data set. The MetaMathQA dataset and MetaMath models at different scales have been open sourced for use by researchers.

• ##Project address: https://meta-math.github.io/
• Paper address: https://arxiv.org/abs/2309.12284
• Data address: https://huggingface.co/datasets/meta-math/MetaMathQA
• Model address: https://huggingface.co/meta-math
• Code address: https://github.com/meta-math/MetaMath

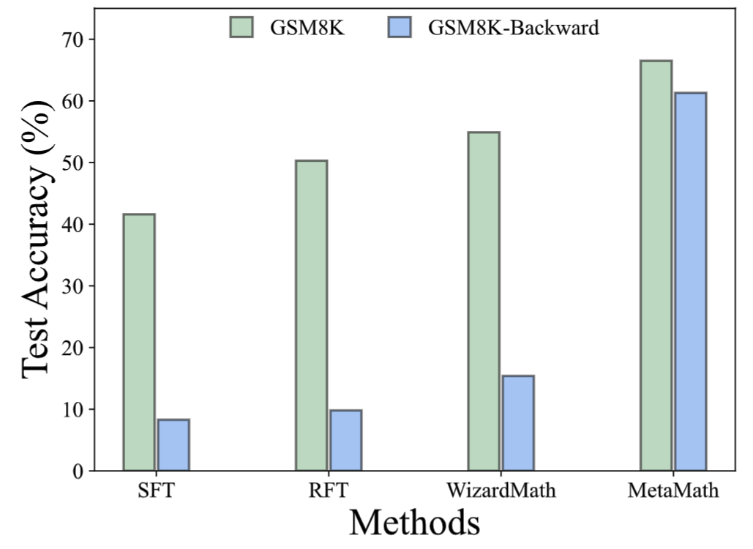
In the GSM8K-Backward data set, we constructed a reverse inference experiment. Experimental results show that compared with methods such as SFT, RFT, and WizardMath, the current method performs poorly on inverse inference problems. In contrast, MetaMath models achieve excellent performance in both forward and backward inference

Method

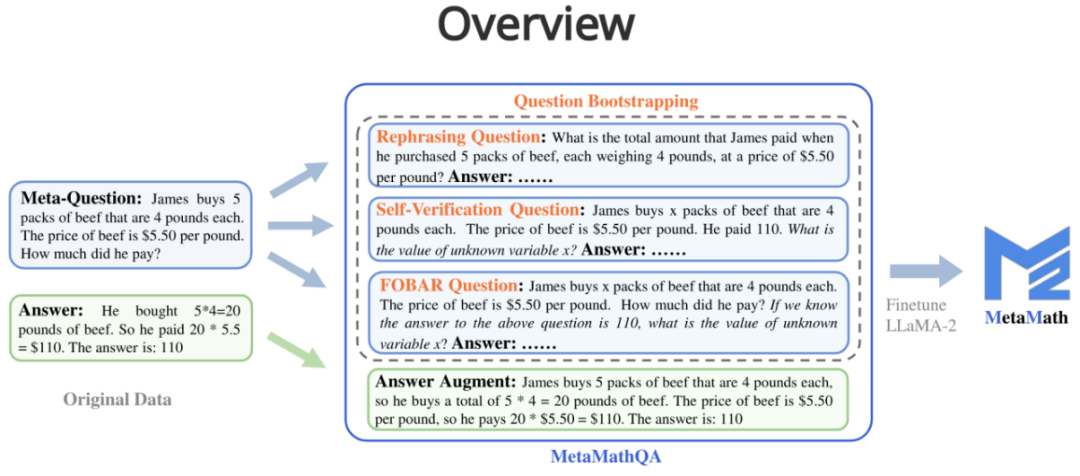
MetaMathQA contains four data augmentation methods:

1. Answer Augmentation (answer Enhancement): Given a problem, a thinking chain that can get the correct result is generated through a large language model as data augmentation.

• Question: James buys 5 packs of beef that are 4 pounds each. The price of beef is $5.50 per pound. How much did he pay?
• Answer: James buys 5 packs of beef that are 4 pounds each, so he buys a total of 5 * 4 = 20 pounds of beef. The price of beef is $5.50 per pound, so he pays 20 * $5.50 = $110. The answer is: 110.

2. Rephrasing Question (question rewriting enhancement): Given meta-question , rewrite the problem through a large language model and generate a thought chain that gets the correct result as data augmentation.

• Question: What is the total amount that James paid when he purchased 5 packs of beef, each weighing 4 pounds, at a price of $5.50 per pound?
• Answer: Each pack of beef weighs 4 pounds, so 5 packs weigh 4 * 5 = 20 pounds in total. The price per pound of beef is $5.50, so the total cost for 20 pounds is 20 * $5.50 = $110. Therefore, James paid a total of $110. The answer is: 110.

##3. FOBAR Question (FOBAR reverse question enhancement)：Given the meta-question, the number in the mask condition is Example: "If we know the answer to the above question is 110, what is the value of unknown variable x?").

• Question: James buys x packs of beef that are 4 pounds each. The price of beef is $5.50 per pound. How much did he pay? If we know the answer to the above question is 110, what is the value of unknown variable x?
• Answer: James buys x packs of beef that are 4 pounds each, so he buys a total of 4x pounds of beef. The price of beef is $5.50 per pound, so the total cost of the beef is 5.50 * 4x = 22x. We are given that the total cost is $110, so we can write: 22x = 110. Dividing both sides by 22, we get: x = 5. The value of x is 5.

4. Self-Verification Question (Self-Verification reverse question enhancement): Based on FOBAR, data augmentation is performed by rewriting the inverse problem part into statements using a large language model (rewritten example: "How much did he pay?" (with the answer 110) was rewritten into "He paid 110").

• Question: James buys x packs of beef that are 4 pounds each. The price of beef is $5.50 per pound. He paid 110. What is the value of unknown variable x ?
• Answer: To solve this problem, we need to determine the value of x, which represents the number of packs of beef that James bought. Each pack of beef weighs 4 pounds and costs $5.50 per pound. The total amount James paid is $110. We can set up the equation as follows: Number of packs of beef * Weight per pack * Price per pound = Total amount paid; x * 4 * $5.50 = $110; Let's simplify and solve for x: 4x * $5.50 = $110; 22x = $110; To isolate x, we divide both sides of the equation by 22: 22x / 22 = $110 / 22; x = $5; The value of x is 5.

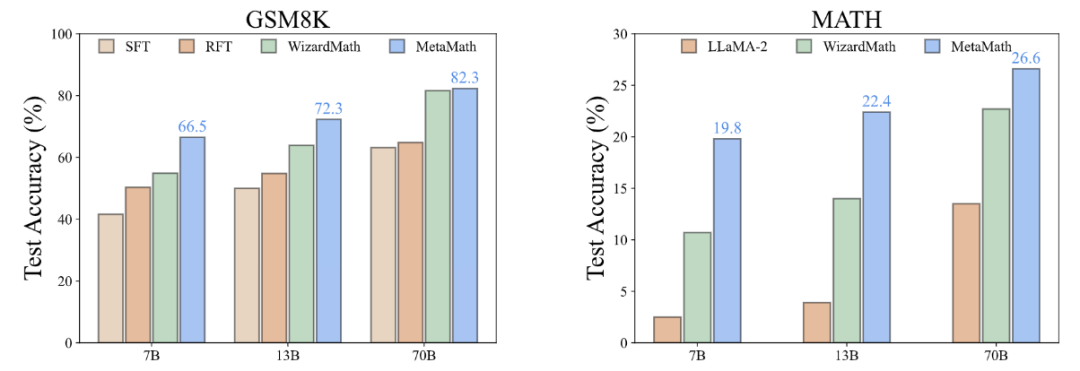
Experimental results

##In two common mathematics Experimental results on inference data sets (GSM8K and MATH) show that MetaMath significantly outperforms existing open source LLM models in performance and does not require the use of external tools (such as code interpreters). Among them, our MetaMath-7B model reaches an accuracy of 66.5% on GSM8K and 19.8% on MATH, which are 11.6% and 9.1% higher than the state-of-the-art models of the same scale respectively. It is particularly worth mentioning that MetaMath-70B achieved an accuracy of 82.3% on GSM8K, exceeding GPT-3.5-Turbo

According to the "Surface Alignment Assumption" [2], The power of large language models comes from pre-training, and data from downstream tasks activates the inherent capabilities of the language model learned during pre-training. Therefore, this raises two important questions: (i) which type of data activates latent knowledge most effectively, and (ii) why is one dataset better at such activation than another?

Why is MetaMathQA useful? Improved the quality of thought chain data (Perplexity)

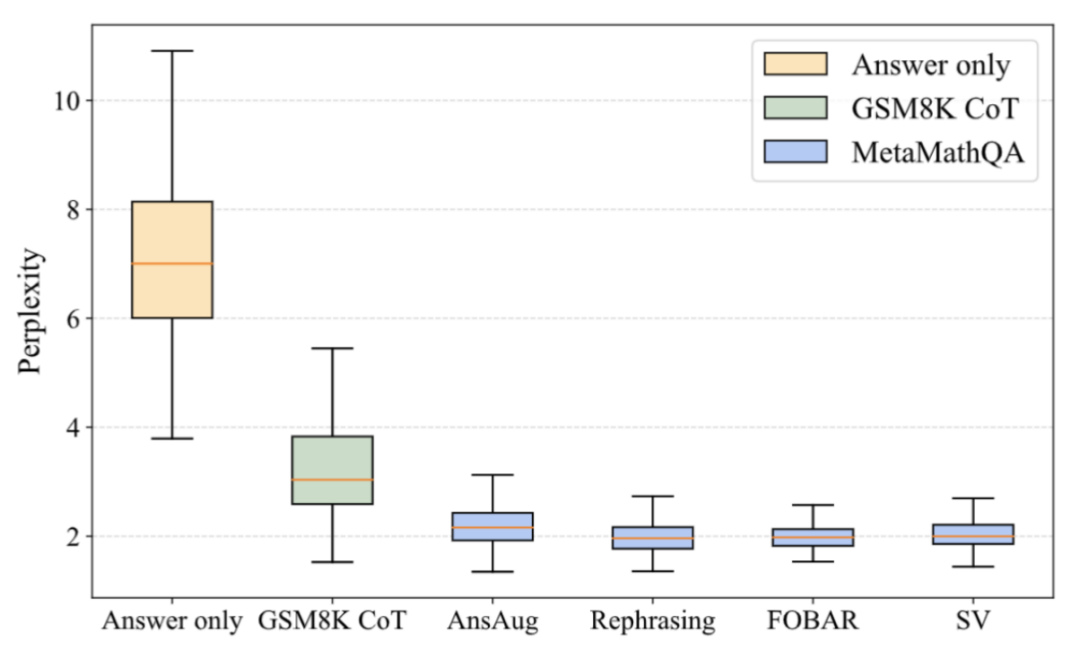##As shown in the figure above, the researchers calculated Perplexity of the LLaMA-2-7B model on answer-only data, GSM8K CoT, and various parts of the MetaMathQA dataset. The perplexity of the MetaMathQA dataset is significantly lower than the other two datasets, indicating that it has higher learnability and may be more helpful in revealing the latent knowledge of the model

Why is MetaMathQA useful? Increased the diversity of thought chain data (Diversity)

By comparing the diversity gain of the data and the accuracy gain of the model, the researchers found that the introduction of the same amount of augmented data by reformulation, FOBAR and SV all brought A significant diversity gain was achieved and the accuracy of the model was significantly improved. In contrast, using answer augmentation alone resulted in significant saturation of accuracy. After the accuracy reaches saturation, adding AnsAug data will only bring limited performance improvement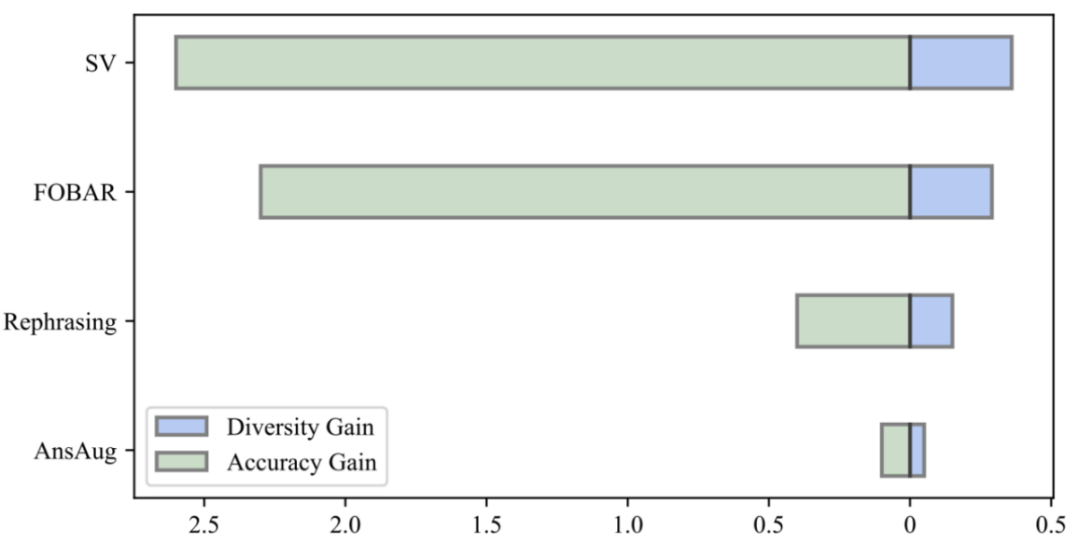

The above is the detailed content of Reverse thinking: MetaMath new mathematical reasoning language model trains large models. For more information, please follow other related articles on the PHP Chinese website!