 Technology peripherals
Technology peripherals AI
AI What is the minimum length of paper tape required to make a Möbius strip? 50-year-old mystery solved
What is the minimum length of paper tape required to make a Möbius strip? 50-year-old mystery solvedWhat is the minimum length of paper tape required to make a Möbius strip? 50-year-old mystery solved
Have you ever made a Mobius strip yourself?


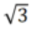 . For example, if the strap length is 1 cm, its width must be greater than
. For example, if the strap length is 1 cm, its width must be greater than  cm.
cm. 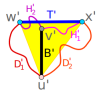
The above is the detailed content of What is the minimum length of paper tape required to make a Möbius strip? 50-year-old mystery solved. For more information, please follow other related articles on the PHP Chinese website!
 The Hidden Dangers Of AI Internal Deployment: Governance Gaps And Catastrophic RisksApr 28, 2025 am 11:12 AM
The Hidden Dangers Of AI Internal Deployment: Governance Gaps And Catastrophic RisksApr 28, 2025 am 11:12 AMThe unchecked internal deployment of advanced AI systems poses significant risks, according to a new report from Apollo Research. This lack of oversight, prevalent among major AI firms, allows for potential catastrophic outcomes, ranging from uncont
 Building The AI PolygraphApr 28, 2025 am 11:11 AM
Building The AI PolygraphApr 28, 2025 am 11:11 AMTraditional lie detectors are outdated. Relying on the pointer connected by the wristband, a lie detector that prints out the subject's vital signs and physical reactions is not accurate in identifying lies. This is why lie detection results are not usually adopted by the court, although it has led to many innocent people being jailed. In contrast, artificial intelligence is a powerful data engine, and its working principle is to observe all aspects. This means that scientists can apply artificial intelligence to applications seeking truth through a variety of ways. One approach is to analyze the vital sign responses of the person being interrogated like a lie detector, but with a more detailed and precise comparative analysis. Another approach is to use linguistic markup to analyze what people actually say and use logic and reasoning. As the saying goes, one lie breeds another lie, and eventually
 Is AI Cleared For Takeoff In The Aerospace Industry?Apr 28, 2025 am 11:10 AM
Is AI Cleared For Takeoff In The Aerospace Industry?Apr 28, 2025 am 11:10 AMThe aerospace industry, a pioneer of innovation, is leveraging AI to tackle its most intricate challenges. Modern aviation's increasing complexity necessitates AI's automation and real-time intelligence capabilities for enhanced safety, reduced oper
 Watching Beijing's Spring Robot RaceApr 28, 2025 am 11:09 AM
Watching Beijing's Spring Robot RaceApr 28, 2025 am 11:09 AMThe rapid development of robotics has brought us a fascinating case study. The N2 robot from Noetix weighs over 40 pounds and is 3 feet tall and is said to be able to backflip. Unitree's G1 robot weighs about twice the size of the N2 and is about 4 feet tall. There are also many smaller humanoid robots participating in the competition, and there is even a robot that is driven forward by a fan. Data interpretation The half marathon attracted more than 12,000 spectators, but only 21 humanoid robots participated. Although the government pointed out that the participating robots conducted "intensive training" before the competition, not all robots completed the entire competition. Champion - Tiangong Ult developed by Beijing Humanoid Robot Innovation Center
 The Mirror Trap: AI Ethics And The Collapse Of Human ImaginationApr 28, 2025 am 11:08 AM
The Mirror Trap: AI Ethics And The Collapse Of Human ImaginationApr 28, 2025 am 11:08 AMArtificial intelligence, in its current form, isn't truly intelligent; it's adept at mimicking and refining existing data. We're not creating artificial intelligence, but rather artificial inference—machines that process information, while humans su
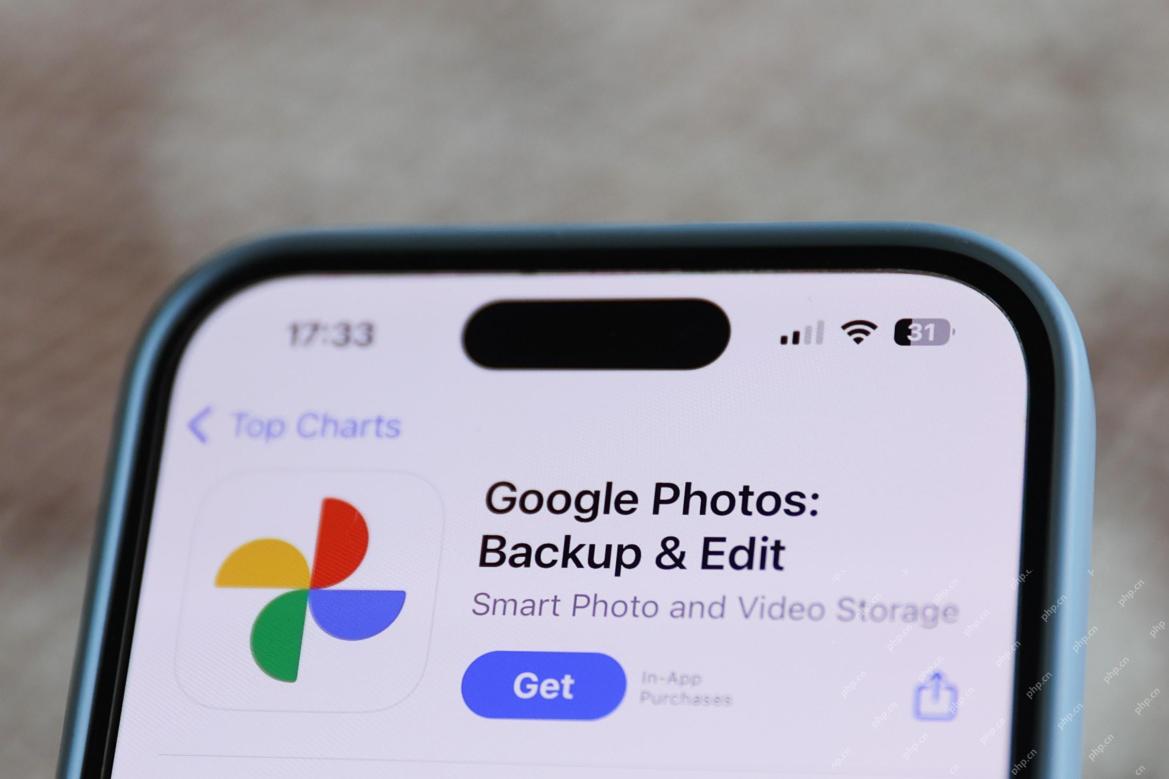 New Google Leak Reveals Handy Google Photos Feature UpdateApr 28, 2025 am 11:07 AM
New Google Leak Reveals Handy Google Photos Feature UpdateApr 28, 2025 am 11:07 AMA report found that an updated interface was hidden in the code for Google Photos Android version 7.26, and each time you view a photo, a row of newly detected face thumbnails are displayed at the bottom of the screen. The new facial thumbnails are missing name tags, so I suspect you need to click on them individually to see more information about each detected person. For now, this feature provides no information other than those people that Google Photos has found in your images. This feature is not available yet, so we don't know how Google will use it accurately. Google can use thumbnails to speed up finding more photos of selected people, or may be used for other purposes, such as selecting the individual to edit. Let's wait and see. As for now
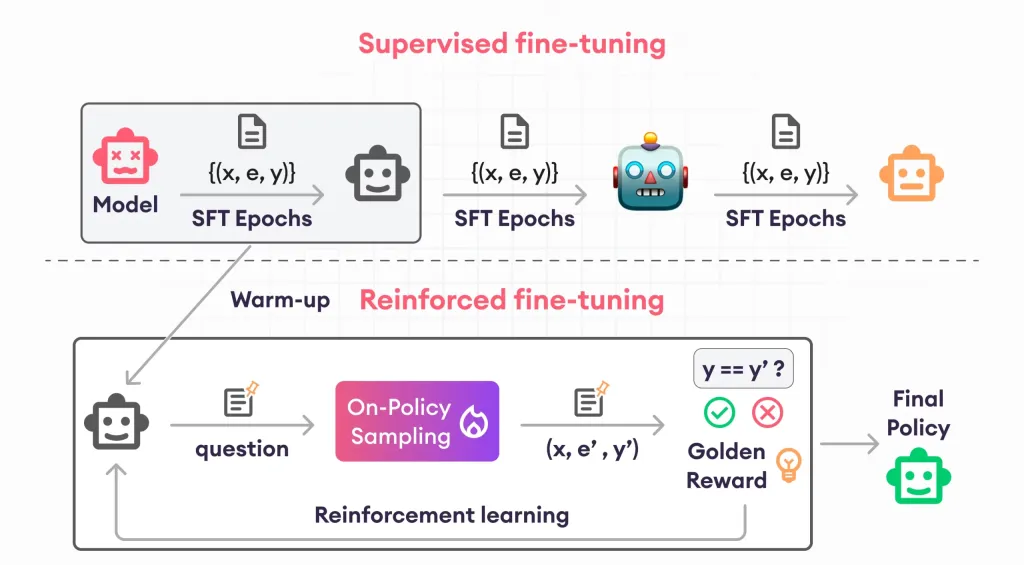 Guide to Reinforcement Finetuning - Analytics VidhyaApr 28, 2025 am 09:30 AM
Guide to Reinforcement Finetuning - Analytics VidhyaApr 28, 2025 am 09:30 AMReinforcement finetuning has shaken up AI development by teaching models to adjust based on human feedback. It blends supervised learning foundations with reward-based updates to make them safer, more accurate, and genuinely help
 Let's Dance: Structured Movement To Fine-Tune Our Human Neural NetsApr 27, 2025 am 11:09 AM
Let's Dance: Structured Movement To Fine-Tune Our Human Neural NetsApr 27, 2025 am 11:09 AMScientists have extensively studied human and simpler neural networks (like those in C. elegans) to understand their functionality. However, a crucial question arises: how do we adapt our own neural networks to work effectively alongside novel AI s


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SublimeText3 Chinese version
Chinese version, very easy to use

Safe Exam Browser
Safe Exam Browser is a secure browser environment for taking online exams securely. This software turns any computer into a secure workstation. It controls access to any utility and prevents students from using unauthorized resources.

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function

SublimeText3 Linux new version
SublimeText3 Linux latest version

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.





