 Backend Development
Backend Development C++
C++ If no more than two points in the plane are collinear, what is the number of triangles?
If no more than two points in the plane are collinear, what is the number of triangles?If no more than two points in the plane are collinear, what is the number of triangles?
Let's see how to count the number of triangles on a plane given n points, and limit the collinear points to no more than two.
Calculating the number of triangles in a plane with no more than two collinear points is a typical problem in computational geometry, which is applied in computer graphics, image processing, and other fields of computer science.
For example, when creating a 2D image from a 3D scene in 3D graphics, the problem may arise of calculating triangles in a plane with no more than two collinear points. In this case, the triangle counting process can be used to determine how many triangles are present in the final 2D image after projecting the 3D scene onto a plane. This allows you to determine the complexity of the scene and increase rendering speed.
In image processing, we may want to count the number of unique objects or shapes in an image, this problem is helpful. In this case, we can represent the image as a collection of points on a plane, and then we can count the number of triangles that can be created between these points by applying triangle counting techniques. We can determine the approximate number of different items or shapes in an image by counting the number of triangles formed.
illustrate
Let us understand this problem through a few examples and try to solve it.
The purpose is to determine how many triangles are formed on a plane with n points such that no more than two points are collinear.
Example -
Assume N is the number of points on the plane.
N = 3
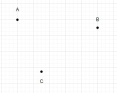
Using these points we can only draw a triangle.
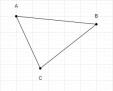
Therefore, the total number of triangles formed using 3 points is 1.
Let N = 4
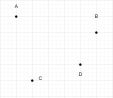
Let's draw a triangle using these four points.
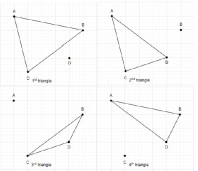
The total number of triangles formed using 4 points is 4.
Let's look at some of the math involved in calculating the number of triangles. This can be obtained using permutations and combinations. To build a triangle, you need 3 points out of the total at a time.
Thus, if a plane contains n points and no more than two of them are collinear, the number of triangles in the plane is given by the following formula.
$$\mathrm{n_{C_{3}}\:=\:\frac{n(n-1)\:(n-2)}{6}}$$
method
The program finds the number of triangles in the plane if no more than two points are collinear, using the following algorithm.
Take the number of points on the plane as input and limit it to no more than two collinear points.
Use the above formula to calculate the total number of triangles.
Print the total number of triangles as output.
Example
C program to calculate the number of triangles in a plane if no more than two points are collinear.
#include <iostream>
using namespace std;
int main() {
int number_of_points = 4;
int number_of_triangle;
number_of_triangle = number_of_points * (number_of_points - 1) * (number_of_points - 2) / 6;
cout << "Total number of triangles formed using " << number_of_points<< " points = " << number_of_triangle << endl;
return 0;
}
Output
Total number of triangles formed using 4 points = 4
Complexity
Time complexity: O(1) because this code performs a fixed number of calculations regardless of the input size.
Space Complexity: O(1) because the code uses a fixed number of variables to store input values and results regardless of the size of the input.
in conclusion
In this article, we try to explain the method to find the total number of possible triangles with n given points, with the constraint that no two points are collinear. I hope this article helps you learn this concept better.
The above is the detailed content of If no more than two points in the plane are collinear, what is the number of triangles?. For more information, please follow other related articles on the PHP Chinese website!
 Debunking the Myths: Is C Really a Dead Language?May 05, 2025 am 12:11 AM
Debunking the Myths: Is C Really a Dead Language?May 05, 2025 am 12:11 AMC is not dead, but has flourished in many key areas: 1) game development, 2) system programming, 3) high-performance computing, 4) browsers and network applications, C is still the mainstream choice, showing its strong vitality and application scenarios.
 C# vs. C : A Comparative Analysis of Programming LanguagesMay 04, 2025 am 12:03 AM
C# vs. C : A Comparative Analysis of Programming LanguagesMay 04, 2025 am 12:03 AMThe main differences between C# and C are syntax, memory management and performance: 1) C# syntax is modern, supports lambda and LINQ, and C retains C features and supports templates. 2) C# automatically manages memory, C needs to be managed manually. 3) C performance is better than C#, but C# performance is also being optimized.
 Building XML Applications with C : Practical ExamplesMay 03, 2025 am 12:16 AM
Building XML Applications with C : Practical ExamplesMay 03, 2025 am 12:16 AMYou can use the TinyXML, Pugixml, or libxml2 libraries to process XML data in C. 1) Parse XML files: Use DOM or SAX methods, DOM is suitable for small files, and SAX is suitable for large files. 2) Generate XML file: convert the data structure into XML format and write to the file. Through these steps, XML data can be effectively managed and manipulated.
 XML in C : Handling Complex Data StructuresMay 02, 2025 am 12:04 AM
XML in C : Handling Complex Data StructuresMay 02, 2025 am 12:04 AMWorking with XML data structures in C can use the TinyXML or pugixml library. 1) Use the pugixml library to parse and generate XML files. 2) Handle complex nested XML elements, such as book information. 3) Optimize XML processing code, and it is recommended to use efficient libraries and streaming parsing. Through these steps, XML data can be processed efficiently.
 C and Performance: Where It Still DominatesMay 01, 2025 am 12:14 AM
C and Performance: Where It Still DominatesMay 01, 2025 am 12:14 AMC still dominates performance optimization because its low-level memory management and efficient execution capabilities make it indispensable in game development, financial transaction systems and embedded systems. Specifically, it is manifested as: 1) In game development, C's low-level memory management and efficient execution capabilities make it the preferred language for game engine development; 2) In financial transaction systems, C's performance advantages ensure extremely low latency and high throughput; 3) In embedded systems, C's low-level memory management and efficient execution capabilities make it very popular in resource-constrained environments.
 C XML Frameworks: Choosing the Right One for YouApr 30, 2025 am 12:01 AM
C XML Frameworks: Choosing the Right One for YouApr 30, 2025 am 12:01 AMThe choice of C XML framework should be based on project requirements. 1) TinyXML is suitable for resource-constrained environments, 2) pugixml is suitable for high-performance requirements, 3) Xerces-C supports complex XMLSchema verification, and performance, ease of use and licenses must be considered when choosing.
 C# vs. C : Choosing the Right Language for Your ProjectApr 29, 2025 am 12:51 AM
C# vs. C : Choosing the Right Language for Your ProjectApr 29, 2025 am 12:51 AMC# is suitable for projects that require development efficiency and type safety, while C is suitable for projects that require high performance and hardware control. 1) C# provides garbage collection and LINQ, suitable for enterprise applications and Windows development. 2)C is known for its high performance and underlying control, and is widely used in gaming and system programming.
 How to optimize codeApr 28, 2025 pm 10:27 PM
How to optimize codeApr 28, 2025 pm 10:27 PMC code optimization can be achieved through the following strategies: 1. Manually manage memory for optimization use; 2. Write code that complies with compiler optimization rules; 3. Select appropriate algorithms and data structures; 4. Use inline functions to reduce call overhead; 5. Apply template metaprogramming to optimize at compile time; 6. Avoid unnecessary copying, use moving semantics and reference parameters; 7. Use const correctly to help compiler optimization; 8. Select appropriate data structures, such as std::vector.


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SublimeText3 Linux new version
SublimeText3 Linux latest version

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

Notepad++7.3.1
Easy-to-use and free code editor

Zend Studio 13.0.1
Powerful PHP integrated development environment

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software






