Home >Backend Development >C++ >What is the largest Reuleaux triangle inside a square inscribed in an ellipse?
What is the largest Reuleaux triangle inside a square inscribed in an ellipse?
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBforward
- 2023-08-29 20:49:051327browse
Here we will see the area of the largest Ruhr triangle inscribed in a square, which in turn is inscribed in an ellipse. We know that the length of the major axis of the ellipse is 2a and the length of the minor axis is 2b. The side length of the square is 'x' and the height of the Luer triangle is h.
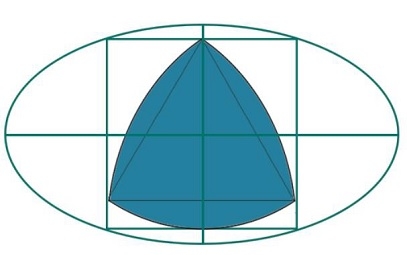
We know that the side length of a square inscribed in an ellipse with a major axis of 2a and a minor axis of 2b is −
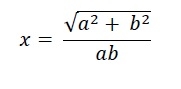
The height of the Ruhr triangle is the same as a. So h = x. Therefore, the area of the Ruhr triangle is −
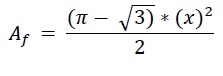 .
.
Example
#include <iostream>
#include <cmath>
using namespace std;
float areaReuleaux(float a, float b) { //a and b are half of major and minor axis of ellipse
if (a < 0 || b < 0) //either a or b is negative it is invalid
return -1;
float x = sqrt((a*a) + (b*b)) / (a*b);
float area = ((3.1415 - sqrt(3)) * (x) * (x))/2;
return area;
}
int main() {
float a = 5;
float b = 4;
cout << "Area of Reuleaux Triangle: " << areaReuleaux(a, b);
}Output
Area of Reuleaux Triangle: 0.0722343
The above is the detailed content of What is the largest Reuleaux triangle inside a square inscribed in an ellipse?. For more information, please follow other related articles on the PHP Chinese website!

