How to use @cache in Python

#What are the magical uses of @cache in Python?

By adopting a caching strategy, space can be converted into time, thereby improving computer system performance. The role of caching in code is to optimize the running speed of the code, although it will increase the memory footprint.

In Python’s built-in module functools, the high-order function cache() is provided to implement caching, which is used as a decorator: @cache.

@cache cache function introduction

In the source code of cache, the description of cache is: Simple lightweight unbounded cache. Sometimes called “memoize”. Translated into Chinese: Simple lightweight unbounded cache. Limit caching. Sometimes called "memoization".

def cache(user_function, /):
    'Simple lightweight unbounded cache.  Sometimes called "memoize".'
    return lru_cache(maxsize=None)(user_function)

cache() has only one line of code, calling the lru_cache() function and passing in a parameter maxsize=None. lru_cache() is also a function in the functools module. Check the source code of lru_cache(). The default value of maxsize is 128, which means that the maximum cached data is 128. If the data exceeds 128, it will be deleted according to the LRU (Longest Unused) algorithm. data. cache() sets maxsize to None, then the LRU feature is disabled and the number of caches can grow infinitely, so it is called "unbounded cache".

lru_cache() uses the LRU (Least Recently Used) algorithm, which has not been used for a long time. This is why there are three letters lru in the function name. The mechanism of the least used algorithm is that assuming a data has not been accessed in the recent period, the possibility of it being accessed in the future is also very small. The LRU algorithm chooses to eliminate the least recently used data and retain those that are frequently used. data.

cache() is new in Python 3.9 version, lru_cache() is new in Python 3.2 version, cache() cancels the limit on the number of caches on the basis of lru_cache(). In fact, It is related to technological progress and the substantial improvement of hardware performance. cache() and lru_cache() are just different versions of the same function.

lru_cache() is essentially a decorator that provides a cache function for the function. It caches the maxsize group of incoming parameters and directly returns the previous result when the function is called with the same parameters next time to save money. The calling time of high overhead or high I/O functions.

@cache application scenarios

Cache has a wide range of application scenarios, such as caching static web content. You can directly add the @cache decorator to the function where users access static web pages.

In some recursive codes, the same parameter is repeatedly passed in to execute the function code. Using cache can avoid repeated calculations and reduce the time complexity of the code.

Next, I will use the Fibonacci sequence as an example to illustrate the role of @cache. If you still have a little understanding of the previous content, I believe you will be enlightened after reading the example.

The Fibonacci sequence refers to a sequence of numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34,..., starting from the third number, each number is The sum of the first two numbers. Most beginners have written code for the Fibonacci sequence. Its implementation is not difficult. In Python, the code is very concise. As follows:

def feibo(n):
    # 第0个数和第1个数为1
    a, b = 1, 1
    for _ in range(n):
        # 将b赋值给a,将a+b赋值给b,循环n次
        a, b = b, a+b
    return a

Of course, there are many ways to implement the code of the Fibonacci sequence (at least five or six). In order to illustrate the application scenario of @cache, this article uses recursive method to write the Fibonacci sequence. code. As follows:

def feibo_recur(n):
    if n < 0:
        return "n小于0无意义"
    # n为0或1时返回1（前两个数为1）
    if n == 0 or n == 1:
        return 1
    # 根据斐波那契数列的定义，其他情况递归返回前两个数之和
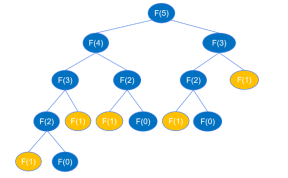
    return feibo_recur(n-1) + feibo_recur(n-2)

When the recursive code is executed, it will recurse all the way to feibo_recur(1) and feibo_recur(0), as shown in the figure below (taking the sixth number as an example).

When finding F(5), you must first find F(4) and F(3). When finding F(4), you must first find F(3) and F( 2),... By analogy, the recursive process is similar to the depth-first traversal of a binary tree. It is known that a binary tree with height k can have up to 2k-1 nodes. According to the above recursive call diagram, the height of the binary tree is n and the nodes are at most 2n-1. That is, the number of recursive function calls is at most 2n-1 times. , so the time complexity of recursion is O(2^n).

When the time complexity is O(2^n), the execution time changes very exaggeratedly as n increases. Let’s actually test it below.

import time
for i in [10, 20, 30, 40]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

Output:

The 10th Fibonacci number: 89
n=10 Cost Time: 0.0
The 20th Fibonacci number: 10946
n=20 Cost Time: 0.0015988349914550781
The 30th Fibonacci number: 1346269
n=30 Cost Time: 0.17051291465759277
The 40th Fibonacci number: 165580141
n=40 Cost Time: 20.90010976791382

It can be seen from the running time that when n is very small, the running time is very fast. As n increases, the running time increases rapidly, especially when n gradually increases to 30 and 40, the running time changes particularly obviously. In order to see the time change pattern more clearly, further tests were conducted.

for i in [41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

Output:

The 41st Fibonacci number: 267914296
n=41 Cost Time: 33.77224683761597
The 42nd Fibonacci number: 433494437
n=42 Cost Time: 55.86398696899414
The 43rd Fibonacci number: 701408733
n=43 Cost Time: 92.55108690261841

从上面的变化可以看到，时间是指数级增长的（大约按1.65的指数增长），这跟时间复杂度为 O(2^n) 相符。按照这个时间复杂度，假如要计算第50个斐波那契数列，差不多要等一个小时，非常不合理，也说明递归的实现方式运算量过大，存在明显的不足。如何解决这种不足，降低运算量呢？接下来看如何进行优化。

根据前面的分析，递归代码运算量大，是因为递归执行时会不断的计算 feibo_recur(n-1) 和 feibo_recur(n-2)，如示例图中，要得到 feibo_recur(5) ，feibo_recur(1) 调用了5次。随着 n 的增大，调用次数呈指数级增长，导致出现大量的重复操作，浪费了许多时间。

假如有一个地方将每个 n 的执行结果记录下来，当作“备忘录”，下次函数再接收到这个相同的参数时，直接从备忘录中获取结果，而不用去执行递归的过程，就可以避免这些重复调用。在 Python 中，可以创建一个字典或列表来当作“备忘录”使用。

temp = {}  # 创建一个空字典，用来记录第i个斐波那契数列的值
def feibo_recur_temp(n):
    if n < 0:
        return "n小于0无意义"
    # n为0或1时返回1（前两个数为1）
    if n == 0 or n == 1:
        return 1
    if n in temp:  # 如果temp字典中有n,则直接返回值,不调用递归代码
        return temp[n]
    else:
        # 如果字典中还没有第n个斐波那契数，则递归计算并保存到字典中
        temp[n] = feibo_recur_temp(n-1) + feibo_recur_temp(n-2)
        return temp[n]

上面的代码中，创建了一个空字典用于存放每个 n 的执行结果。每次调用函数，都先查看字典中是否有记录，如果有记录就直接返回，没有记录就递归执行并将结果记录到字典中，再从字典中返回结果。这里的递归其实都只执行了一次计算，并没有真正的递归，如第一次传入 n 等于 5，执行 feibo_recur_temp(5)，会递归执行 n 等于 4, 3, 2, 1, 0 的情况，每个 n 计算过一次后 temp 中都有了记录，后面都是直接到 temp 中取数相加。每个 n 都是从temp中取 n-1 和 n-2 的值来相加，执行一次计算，所以时间复杂度是 O(n) 。

下面看一下代码的运行时间。

for i in [10, 20, 30, 40, 41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur_temp(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)
print(temp)

Output:

第10个斐波那契数: 89
n=10 Cost Time:  0.0
第20个斐波那契数: 10946
n=20 Cost Time:  0.0
第30个斐波那契数: 1346269
n=30 Cost Time:  0.0
第40个斐波那契数: 165580141
n=40 Cost Time:  0.0
第41个斐波那契数: 267914296
n=41 Cost Time:  0.0
第42个斐波那契数: 433494437
n=42 Cost Time:  0.0
第43个斐波那契数: 701408733
n=43 Cost Time:  0.0
{2: 2, 3: 3, 4: 5, 5: 8, 6: 13, 7: 21, 8: 34, 9: 55, 10: 89, 11: 144, 12: 233, 13: 377, 14: 610, 15: 987, 16: 1597, 17: 2584, 18: 4181, 19: 6765, 20: 10946, 21: 17711, 22: 28657, 23: 46368, 24: 75025, 25: 121393, 26: 196418, 27: 317811, 28: 514229, 29: 832040, 30: 1346269, 31: 2178309, 32: 3524578, 33: 5702887, 34: 9227465, 35: 14930352, 36: 24157817, 37: 39088169, 38: 63245986, 39: 102334155, 40: 165580141, 41: 267914296, 42: 433494437, 43: 701408733}

可以观察到，代码的运行时间已经减少到小数点后很多位了（时间过短，只显示了0.0）。然而，temp 字典存储了每个数字的斐波那契数，这需要使用额外的内存空间，以换取更高的时间效率。

上面的代码也可以用列表来当“备忘录”，代码如下。

temp = [1, 1]
def feibo_recur_temp(n):
    if n < 0:
        return "n小于0无意义"
    if n == 0 or n == 1:
        return 1
    if n < len(temp):
        return temp[n]
    else:
        # 第一次执行时，将结果保存到列表中，后续直接从列表中取
        temp.append(feibo_recur_temp(n-1) + feibo_recur_temp(n-2))
        return temp[n]

现在，已经剖析了递归代码重复执行带来的时间复杂度问题，也给出了优化时间复杂度的方法，让我们将注意力转回到本文介绍的 @cache 装饰器。@cache 装饰器的作用是将函数的执行结果缓存，在下次以相同参数调用函数时直接返回上一次的结果，与上面的优化方式完全一致。

所以，只需要在递归函数上加 @cache 装饰器，递归的重复执行就可以解决，时间复杂度就能从 O(2^n) 降为 O(n) 。代码如下：

from functools import cache
@cache
def feibo_recur(n):
    if n < 0:
        return "n小于0无意义"
    if n == 0 or n == 1:
        return 1
    return feibo_recur(n-1) + feibo_recur(n-2)

使用 @cache 装饰器，可以让代码更简洁优雅，并且让你专注于处理业务逻辑，而不需要自己实现缓存。下面看一下实际的运行时间。

for i in [10, 20, 30, 40, 41, 42, 43]:
    start = time.time()
    print(f'第{i}个斐波那契数:', feibo_recur(i))
    end = time.time()
    print(f'n={i} Cost Time: ', end - start)

Output:

第10个斐波那契数: 89
n=10 Cost Time:  0.0
第20个斐波那契数: 10946
n=20 Cost Time:  0.0
第30个斐波那契数: 1346269
n=30 Cost Time:  0.0
第40个斐波那契数: 165580141
n=40 Cost Time:  0.0
第41个斐波那契数: 267914296
n=41 Cost Time:  0.0
第42个斐波那契数: 433494437
n=42 Cost Time:  0.0
第43个斐波那契数: 701408733
n=43 Cost Time:  0.0

完美地解决了问题，所有运行时间都被精确到了小数点后数位（即使只显示 0.0），非常巧妙。若今后遇到类似情形，可以直接采用 @cache 实现缓存功能，通过“记忆化”处理。

补充：Python @cache装饰器

@cache和@lru_cache(maxsize=None)可以用来寄存函数对已处理参数的结果，以便遇到相同参数可以直接给出答案。前者无限制存储数量，而后者通过设定maxsize限制存储数量的上限。

例：

@lru_cache(maxsize=None) # 等价于@cache
def test(a,b):
    print('开始计算a+b的值...')
    return a + b

可以用来做某些递归、动态规划。比如斐波那契数列的各项值从小到大输出。其实类似用数组保存前项的结果，都需要额外的空间。不过用装饰器可以省略额外空间代码，减少了出错的风险。

The above is the detailed content of How to use @cache in Python. For more information, please follow other related articles on the PHP Chinese website!