Use Java language to implement bubble sorting and selection sorting algorithms

BubbleSort method

Bubble sorting method The bubble algorithm is talked about a lot in traditional C language textbooks. It is a relatively stable sorting algorithm. When you use this sorting algorithm, you can think of its implementation form from its name. When it comes to bubbling, the first thing that comes to mind is a small fish swimming in the water, spitting out a string of small bubbles and rising to the surface of the water. In fact, the bubble sorting method is the same as popping bubbles. It only spits out one at a time, and spits them out one after another continuously. The central idea of ​​the bubble sort algorithm is to compare two adjacent numbers and then exchange positions according to size requirements. Let’s start with the simplest array of two elements and draw inferences from there. Suppose there are only two elements inside an array "int array = {8, 0};". When sorting them, we only need to make one judgment to know which element is larger and which element is smaller. Assuming that we arrange from small to large, the result of the arrangement should be "array = {0, 8};". Let’s look at an array with three elements. Suppose there are only two elements inside an array "int array = {8, 0, 1};". Then we still perform a pairwise comparison. In the first comparison, we can conclude that the array should be "array = {0, 1, 8};", and only one comparison is needed to complete the sorting of the array. But if the array changes the position of the elements, that is, "int array = {8, 1, 0};", then let's take a look again. The first pairwise comparison of elements becomes "array = {1, 0, 8} ;", so when encountering this extreme situation, the bubble method cannot complete the sorting with one comparison, then a second comparison should be performed. Finally, in the second comparison we can get the result "array = {0, 1, 8}; "Let's look at the sorting of the array when there are four elements. This time we take an extreme case, that is, changing an array arranged from large to small into an array arranged from small to large. The array is "int array = {9, 8, 1, 0};". Then at this time, the first comparison of two adjacent elements can yield "array = {8, 1, 0, 9};", and the second comparison of adjacent elements can yield "array = {1, 0, 8, 9};", the third pairwise comparison can yield "array = {0, 1, 8, 9};". Based on the above analysis, we can know that if an array has n elements that need to be sorted, the extreme case of sorting should be n-1 times. The specific sorting process is as follows.

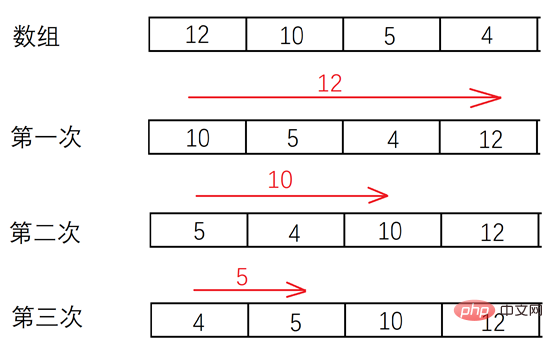
Bubble sorting process
So based on the above analysis, we can write the code as follows .

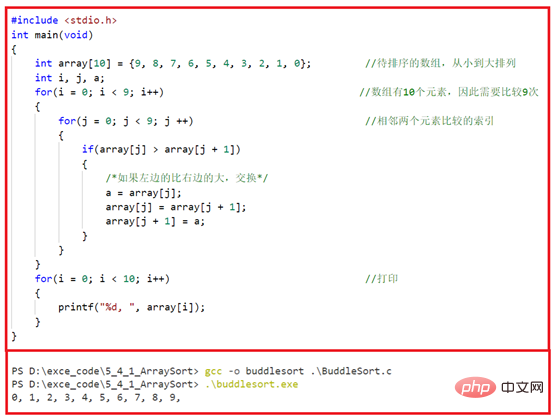
Next, we modify the program so that it prints out the process of comparing two adjacent elements at each step, as shown in Figure 5-4-3 shown. We can see that larger elements will slowly "float" to the top of the sequence through exchange (arranged in ascending or descending order), just like a string of bubbles spit out by a little goldfish in the water and slowly surface, hence the name "Bubble Sort".

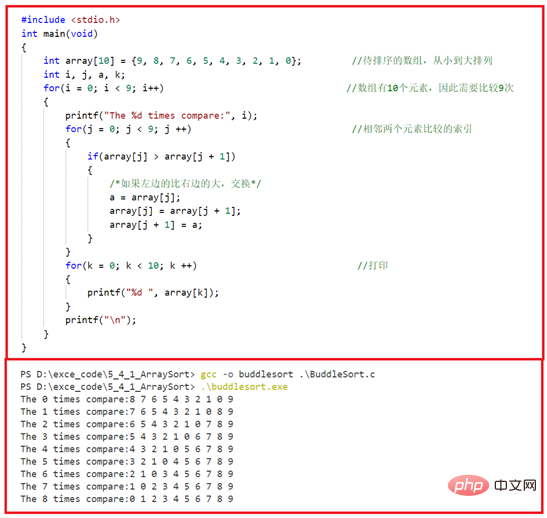
Bubble sorting single-step printing

Selection sorting method

Select Sorting selection sorting, commonly known as "biting the bullet sorting", of course, this "biting the bullet sorting" is the name I gave it, because it is the most intuitive sorting method and perfectly interprets the four words "violent aesthetics". To understand selection sorting, first imagine how the teacher arranges the teams in physical education class in elementary school. First, randomly select a student among the children who the teacher thinks is the shortest and let him be the leader. Then compare the other students with him in turn. If he is taller, he will be placed behind him. If he is shorter, he will be placed in front. Then visually inspect the second one, and so on. Of course, the above paragraph describes the inner thoughts of the physical education teacher. When we sort the array, we can also use this method. We can first designate a vanguard. Suppose we want to arrange from small to large, then we first assume that the first element is the smallest element in the array, and then compare it with the remaining elements respectively. If it is found to be smaller than it, then Interchange itself with that element. In this way, you only need to traverse the entire array and put the smallest element at the position of the first element. As follows.

Select sort and do a traversal comparison

In the above figure, we use the first traversal comparison to select the smallest element Arranged to the left end of the array, what we need to do next is to compare the remaining 9 elements at once, find the minimum value, and then put it to the right of 0, and so on. Finally, we can write as shown in the figure below selection sorting procedure.

The above is the detailed content of Use Java language to implement bubble sorting and selection sorting algorithms. For more information, please follow other related articles on the PHP Chinese website!