How to use Java data structures and algorithms to implement recursion and backtracking

1. What is recursion?

Simply put: Recursion means that the method calls itself, passing in different variables each time it is called. Recursion helps programmers solve complex problems and makes the code concise.

Look at a practical application scenario, maze problem (backtracking), recursion (Recursion)

I will list two small cases. To help you understand recursion, here is a review of the recursive calling mechanism

• Print problem

• Factorial problem

public static void test(int n) {
    if (n > 2) {
	    test(n - 1);
    }
    System.out.println("n=" + n);
}
 
public static int factorial(int n) {
    if (n == 1) {
        return 1;
    } else {
        return factorial(n - 1) * n;
    }
}

What kind of problems is recursion used to solve?

• Various mathematical problems such as: 8 queens problem, Tower of Hanoi, factorial problem, maze Problem, ball and basket problem (google programming competition).

• Recursion is also used in various algorithms, such as quick sort, merge sort, binary search, divide and conquer algorithm, etc.

• The problem that will be solved with the stack-->The code is relatively concise.

Important rules to follow for recursion

• When a method is executed, a new protected independent space (stack space) is created.

• The local variables of the method are independent and will not affect each other, such as the n variable.

• If a reference type variable (such as an array) is used in the method, the data of the reference type will be shared.

• Recursion must approach the conditions for exiting the recursion, otherwise it will be infinite recursion, a StackOverflowError will appear, and you will be dead :).

• When a method completes execution or encounters return, it will return. Whoever calls it will return the result to whoever calls it. At the same time, when the method completes execution or returns, the method will also return. The execution is completed.

2. Code Case 1 - Maze Problem

Description: The path obtained by the ball is the same as the path finding set by the programmer The strategy is related to: the order of up, down, left, and right when finding the path is related. When you get the path of the ball, you can first use (bottom right, top left), and then change it to (top right, bottom left) to see if the path changes. Test for backtracking phenomena.

package com.szh.recursion;
 
/**
 * 走迷宫问题
 */
public class MiGong {
 
    //使用递归回溯来给小球找路, 说明:
    //1. map 表示地图
    //2. i,j 表示从地图的哪个位置开始出发 (1,1)
    //3. 如果小球能到 map[6][5] 位置，则说明通路找到.
    //4. 约定：当 map[i][j] 为 0 表示该点没有走过; 当为 1 表示墙; 2 表示通路可以走;
    //5. 在走迷宫时，需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通，再回溯
    public static boolean setWay(int[][] map, int i, int j) {
        //此时走到了迷宫终点
        if (map[6][5] == 2) {
            return true;
        } else {
            if (map[i][j] == 0) { //如果当前这个点还没有走过
                //按照策略 下->右->上->左  走
                map[i][j] = 2;
                if (setWay(map, i + 1, j)) { //下
                    return true;
                } else if (setWay(map, i, j + 1)) { //右
                    return true;
                } else if (setWay(map, i - 1, j)) { //上
                    return true;
                } else { //左
                    return true;
                }
            } else { //map[i][j] != 0, 即只能为1、2。 1表示墙（无法走），2表示已经走过了，所以此时直接返回false
                return false;
            }
        }
    }
 
    //修改找路的策略，改成 上->右->下->左
    public static boolean setWay2(int[][] map, int i, int j) {
        if(map[6][5] == 2) { // 通路已经找到ok
            return true;
        } else {
            if(map[i][j] == 0) { //如果当前这个点还没有走过
                //按照策略 上->右->下->左
                map[i][j] = 2;
                if(setWay2(map, i - 1, j)) { //上
                    return true;
                } else if (setWay2(map, i, j + 1)) { //右
                    return true;
                } else if (setWay2(map, i + 1, j)) { //下
                    return true;
                } else { //左
                    return true;
                }
            } else {
                return false;
            }
        }
    }
 
    public static void main(String[] args) {
        //先创建一个二维数组，模拟迷宫 (地图)
        int[][] map = new int[8][7];
        //使用迷宫中的部分格子表示墙体（置1）
        //第一行和最后一行置为1
        for (int i = 0; i < 7; i++) {
            map[0][i] = 1;
            map[7][i] = 1;
        }
        //第一列和最后一列置为1
        for (int i = 0; i < 8; i++) {
            map[i][0] = 1;
            map[i][6] = 1;
        }
        //多添加两块墙体
        map[3][1] = 1;
        map[3][2] = 1;
//      map[1][2] = 1;
//		map[2][2] = 1;
        //输出地图查看
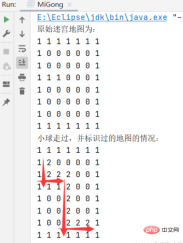
        System.out.println("原始迷宫地图为：");
        for (int i = 0; i < 8; i++) {
            for (int j = 0; j < 7; j++) {
                System.out.print(map[i][j] + " ");
            }
            System.out.println();
        }
 
        //使用递归回溯走迷宫
        setWay(map, 1, 1);
//        setWay2(map, 1, 1);
        System.out.println("小球走过，并标识过的地图的情况：");
        for (int i = 0; i < 8; i++) {
            for (int j = 0; j < 7; j++) {
                System.out.print(map[i][j] + " ");
            }
            System.out.println();
        }
    }
}

3. Code Case 2 - The Eight Queens Problem

The Eight Queens Problem is an ancient and famous The problem is a typical case of backtracking algorithm. This problem was raised by international chess player Max Bethel in 1848: Place eight queens on an 8×8 grid chess so that they cannot attack each other, that is, no two queens can be in the same position. How many ways are there in rows, columns or diagonals?

The first queen is placed in the first row and first column first.

Place the second queen in the second row and first column, and then determine whether it is OK. If not, continue to place it in the second column and third column, and then put all the columns in order to find a suitable one. .

Continue to the third queen, or the first column, the second column... until the 8th queen can be placed in a non-conflicting position, it can be regarded as a correct solution.

When a correct solution is obtained, when the stack rolls back to the previous stack, it will start backtracking, that is, put the first queen in the first column and get all the correct solutions.

Then go back and continue placing the first queen in the second column, and then continue to execute steps 1, 2, 3, and 4 in a loop.

package com.szh.recursion;
 
/**
 * 八皇后问题
 */
public class Queue8 {
 
    //定义max表示共有多少个皇后
    private int max = 8;
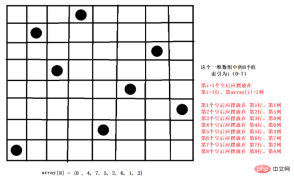
    //定义数组，保存皇后放置的位置结果，比如 arr = {0, 4, 7, 5, 2, 6, 1, 3}
    int[] array = new int[max];
    //共有多少种解法
    private static int count = 0;
    //共有多少次冲突
    private static int judgeCount = 0;
 
    //编写一个方法，放置第n个皇后
    //特别注意： check 是 每一次递归时，进入到check中都有  for(int i = 0; i < max; i++)，因此会有回溯
    private void check(int n) {
        if (n == max) { //n = 8 , 表示这8个皇后已经全部放好了
            print();
            return;
        }
        //依次放入皇后，并判断是否冲突
        for (int i = 0; i < max; i++) {
            //先把当前这个皇后 n , 放到该行的第1列
            array[n] = i;
            //判断当放置第n个皇后到i列时，是否冲突
            if (judge(n)) { // 不冲突
                //接着放n+1个皇后,即开始递归
                check(n + 1);
            }
            //如果冲突，就继续执行 array[n] = i; 即将第n个皇后，放置在本行第i列向后的那一列
        }
    }
 
    //查看当我们放置第n个皇后, 就去检测该皇后是否和前面已经摆放的n-1个皇后冲突
    private boolean judge(int n) {
        //每摆放一个皇后，就循环去和之前摆好的皇后位置相比较，看是否冲突
        for (int i = 0; i < n; i++) {
            //1. array[i] == array[n]  表示判断 第n个皇后是否和前面的n-1个皇后在同一列
            //2. Math.abs(n-i) == Math.abs(array[n] - array[i]) 表示判断第n个皇后是否和第i皇后是否在同一斜线
            //3. 判断是否在同一行, 没有必要，n 表示第几个皇后，这个值每次都在递增，所以必然不在同一行
            if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {
                judgeCount++;
                return false;
            }
        }
        return true;
    }
 
    //打印皇后摆放的具体位置
    private void print() {
        count++;
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + " ");
        }
        System.out.println();
    }
 
    public static void main(String[] args) {
        Queue8 queue8 = new Queue8();
        queue8.check(0);
        System.out.printf("一共有%d解法\n", count);
        System.out.printf("一共判断冲突的次数%d次", judgeCount);
    }
}

In fact, you can see the backtracking process by debugging the code, so I won’t say more.

The above is the detailed content of How to use Java data structures and algorithms to implement recursion and backtracking. For more information, please follow other related articles on the PHP Chinese website!