How to implement dichotomy in Java

In an ordered array, find whether a certain number exists

##Idea:

• Since it is an ordered array, you can first get the midpoint position, and the midpoint can divide the array into left and right halves.

• If the value of the midpoint position is equal to the target value, return the midpoint position directly.

• If the value of the midpoint position is less than the target value, go to the left side of the midpoint of the array and search in the same way.

• If the value of the midpoint position is greater than the target value, take the right side of the midpoint of the array and search in the same way.

• If not found at the end, return: -1.

Code

class Solution {
    public int search(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
                return m;
            } else if (arr[m] > t) {
                r = m - 1;
            } else {
                l = m + 1;
            }
        }
        return -1;
    }
}

Time complexity

O(logN).

In an ordered array, find the leftmost position that is greater than or equal to a certain number

Example 1:

Input: nums = [1,3,5,6], target = 5

Output: 2

Explanation: If you want to insert the element 5 into the array

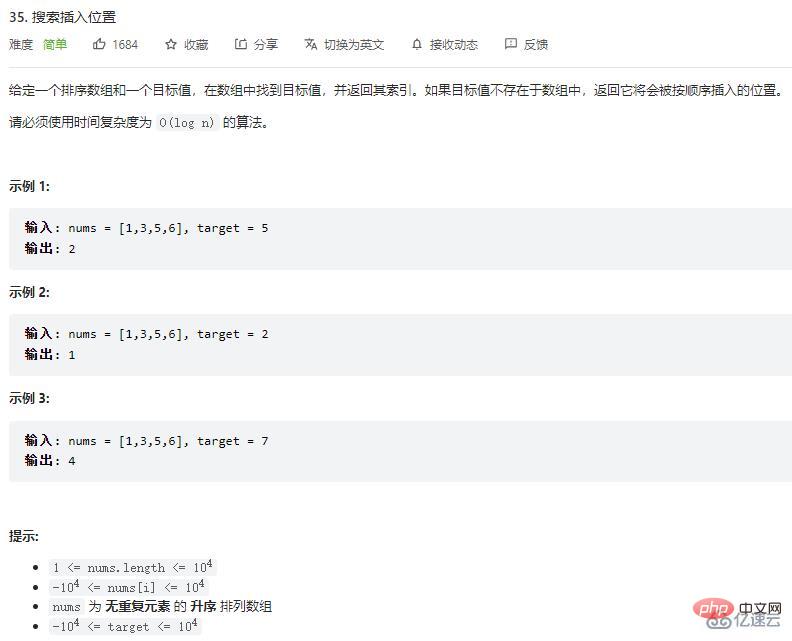
num, It should be inserted between element 3 and element 5, that is, position 2.

Example 2:

Input: nums = [1,3,5,6], target = 2

Output: 1

Explanation: If To insert element 2 into the array

num, it should be inserted at the position between element 1 and element 3, that is, position 1.

Example 3:

Input: nums = [1,3,5,6], target = 7

Output: 4

Explanation: If To insert the element 7 into the array

num, it should be inserted at the end of the array, that is, at position 4.

As you can know from the above example, this question is essentially asking

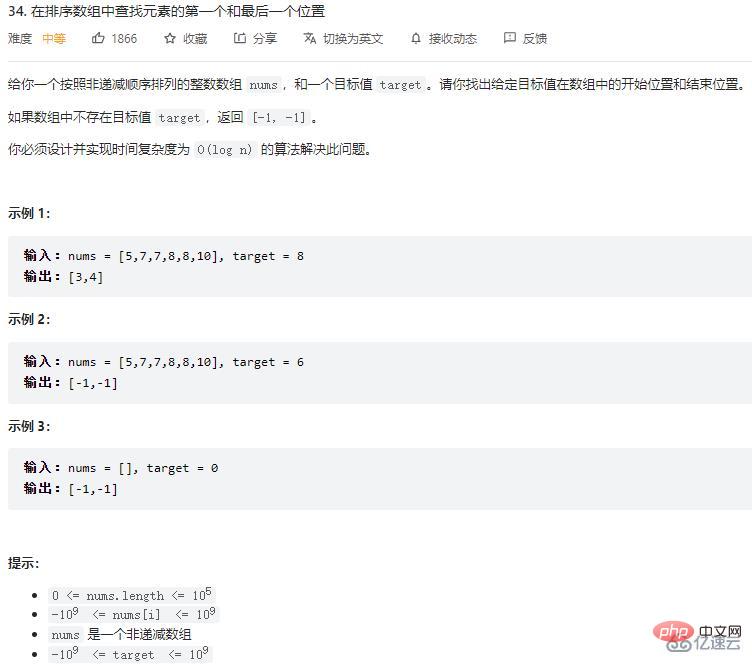
In an ordered array, find the leftmost position that is greater than or equal to a certain number. If it does not exist, return the length of the array (representing Insert at the end position)

We only need to make simple changes based on the above example. In the above example, if we find the position that meets the conditions, we can directly

return

if (arr[m] == t) {
    return m;
}

In this question, because we need to find the leftmost position, when

encounters equality, we only need to record the position first, without returning directly, and then continue to search on the left Is there any position further to the left that meets the conditions?

At the same time, when encountering

arr[m] > t, you also need to record the m position at this time, because this may also is a location that satisfies the conditions.

Code:

class Solution {
    public static int searchInsert(int[] arr, int t) {
        int ans = arr.length;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l)>>1);
            if (arr[m] >= t) {
                ans = m;
                r = m - 1;
            } else  {
                l = m + 1;
            } 
        }
        return ans;
    }
}

The time complexity of the entire algorithm is

O(logN).

Find the first and last position of the element in the sorted array

Ideas

This question is also solved using binary division. When an element is found through binary division, do not rush back, but continue to search to the left (right) to see if you can find a matching value further to the left (right).

The code is as follows:

class Solution {
    public static int[] searchRange(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return new int[]{-1, -1};
        }
        return new int[]{left(arr,t),right(arr,t)};   
    }
    public static int left(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int ans = -1;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
               ans = m;
               r = m - 1;
            } else if (arr[m] < t) {
                l = m +1;
            } else {
                // arr[m] > t
                r = m - 1;
            }
        }
        return ans;
    }
    public static int right(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int ans = -1;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
               ans = m;
               l = m + 1;
            } else if (arr[m] < t) {
                l = m +1;
            } else {
                // arr[m] > t
                r = m - 1;
            }
        }
        return ans;
    }
}

Time complexity

O(logN).

Local maximum problem

Idea

Assume that the length of the array is

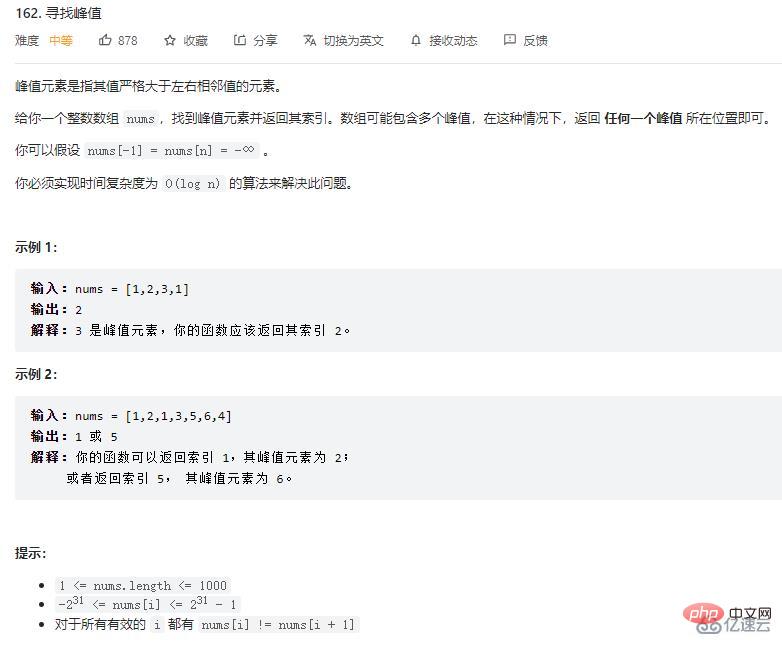
N, first determine 0 Are the number at position and the number at position N-1 the peak position? The

0 position only needs to be compared with the 1 position. If the 0 position is larger, the 0 position It is the peak position and can be returned directly. The

N-1 position only needs to be compared with the N-2 position. If the N-1 position is larger, Position N-1 is the peak position and can be returned directly.

If the

0 position and N-1 are both minimum values ​​in the last round of comparison, then the array must look like the following:

As can be seen from the above figure, the

[0..1] interval is a growth trend, [N-2...N-1] Within the range is a downward trend.

Then the peak position must appear between

[1...N-2].

At this time, you can find the peak position by

bisection, first go to the midpoint position, assuming it is mid, if the value of the midpoint position is greater than the value of the left and right sides Duda:

arr[mid] > arr[mid+1] && arr[mid] > arr[mid-1]

then the

mid position is the peak position and returns directly.

Otherwise, there are two situations as follows:

Case 1: The value of mid position is smaller than the value of mid - 1 position

The trend is as follows:

will continue to divide into two points within the

[1...(mid-1)] interval.

Case 2: The value of the mid position is smaller than the value of the mid 1 position

The trend is:

则在[(mid+1)...(N-2)]区间内继续上述二分。

完整代码

public class LeetCode_0162_FindPeakElement {
    public static int findPeakElement(int[] nums) {
        if (nums.length == 1) {
            return 0;
        }
        int l = 0;
        int r = nums.length - 1;
        if (nums[l] > nums[l + 1]) {
            return l;
        }
        if (nums[r] > nums[r - 1]) {
            return r;
        }
        l = l + 1;
        r = r - 1;
        while (l <= r) {
            int mid = l + ((r - l) >> 1);
            if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
                return mid;
            }
            if (nums[mid] < nums[mid + 1]) {
                l = mid + 1;
            } else if (nums[mid] < nums[mid - 1]) {
                r = mid - 1;
            }
        }
        return -1;
    }
}

时间复杂度O(logN)。

The above is the detailed content of How to implement dichotomy in Java. For more information, please follow other related articles on the PHP Chinese website!