 Technology peripherals
Technology peripherals AI
AI Unconventional Splitting Techniques for Time Series Machine Learning Datasets
Unconventional Splitting Techniques for Time Series Machine Learning DatasetsUnconventional Splitting Techniques for Time Series Machine Learning Datasets
One attempt to ensure that a machine learning model generalizes in unknown environments is to split the data. This can be achieved in a variety of ways, from 3-way (train, test, evaluation) splits to cross-validated k-splits. The basic principle is that by training a machine learning model on a subset of data and evaluating it on unknown data, you can better reason about whether the model was underfitting or overfitting during training.
For most jobs, a simple 3-way is sufficient. In real production, splitting methods often require more complex methods to ensure generalization issues. These splits are more complex because they are derived from actual data rather than the data structures on which ordinary splitting methods are based. This article attempts to explain some unconventional ways of splitting data in machine learning development, and the reasons behind them.
Let’s start with the dataset
For simplicity, let’s use a tabular format to represent a simple multivariate time series dataset. The data consists of 3 numeric features, 1 categorical feature and 1 timestamp feature. Here’s the visualization:

# This type of dataset is common across many use cases and industries for machine learning. A specific example is time-streamed data transmitted from multiple sensors on a factory floor. The categorical variable will be the ID of the machine, the numeric feature will be the information the sensor is recording (e.g. pressure, temperature, etc.), and the timestamp will be the time the data was transferred and recorded in the database.
Split
Suppose you received this dataset as a csv file from the data engineering department and were tasked with writing a classification or regression model. In this case, the label can be any feature or extra column. The first thing to do is to split the data into meaningful subsets.
For convenience, you can simply split it into a training set and a test set. Immediately the problem arises, simple splitting of the data will not work here: the data is composed of multiple sensor data streams indexed by time. So, how to split the data so that the order is maintained and the subsequent machine learning model has good generalization?
Another view of the data
What we can do The most straightforward transformation is to represent the data for each classification class (in our running example, visualizing the data for each machine). This will produce the following result:

Horizontal Split
Grouping makes the splitting problem a little easier, and it's largely up to you Assumptions. You may ask: How does a machine learning model trained on one group generalize to other groups, that is, if it is trained on class_1, class_2, and class_3 time streams, how will the model perform on class_4 and class_5 time streams? ?The following is a visualization of this split:

The above split method is what I call horizontal splitting. In most machine learning libraries, this split is easily achieved by simply grouping by categorical features and partitioning along the categories. By training with this split, the model has gathered information that generalizes across unknown groupings.
It is worth noting that splitting does not use time as the basis for splitting itself. However, it can be assumed that you will also split by time ordering of each time stream to maintain this relationship in the data. This brings us to the next split.
vertical split
But what if you want to span time itself? For most time series modeling, the common ways to split the data are past and future. That is, comparing the historical data of the training set with the data of the evaluation set. The hypothesis in this case is: How does a machine learning model trained on each group's historical data generalize to each group's future data? This question can be answered by what is called vertical splitting:

Successful training of this split will show that the model is able to extract patterns in the time stream it has seen and make accurate predictions about future behavior. However, this by itself does not indicate that the model generalizes well to other temporal streams from different groups.
Of course, your multiple time streams must now be sorted individually, so we still need to group. But this time, instead of crossing groups, we draw samples from each group in past and put them into train, and put the future group into eval accordingly. In this idealized example, all time streams have the same length, i.e. each time stream has exactly the same number of data points. However, in the real world, this may not be the case - so you need a system to index each group for splitting.
Hybrid splitting
You may be wondering, can they generate a model that can generalize well under the constraints of both horizontal and vertical splitting? In this case, the hypothesis would be: How does a machine learning model trained on some groups of historical data generalize to future data of those groups and to all data of other groups? A visualization of this hybrid split would look like this:

Of course, if the model training is successful, this model will definitely be more robust in the real world than other models. Not only can it demonstrate that it has seen learning patterns for some groups, but it can also demonstrate that it has acquired information that generalizes across groups. This could be useful if we were to add more similar machines to the factory in the future.
Multidimensional splitting
The concepts of horizontal and vertical splitting can be generalized to many dimensions. For example, you may want to group based on two categorical features instead of one to further isolate subgroups in your data and sort them by subgroups. There may also be complex logic in the middle to filter groups with small sample sizes, as well as other business-level logic related to the domain.
Conclusion
This hypothetical example serves to illustrate the endless possibilities of the various machine learning splits that can be created. Just as it’s important to ensure fairness in machine learning when evaluating models, it’s equally important to spend enough time considering partitioning your dataset and its consequences for biasing downstream models.
The above is the detailed content of Unconventional Splitting Techniques for Time Series Machine Learning Datasets. For more information, please follow other related articles on the PHP Chinese website!
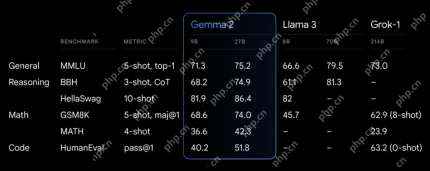 Exploring the Capabilities of Google's Gemma 2 ModelsApr 22, 2025 am 11:26 AM
Exploring the Capabilities of Google's Gemma 2 ModelsApr 22, 2025 am 11:26 AMGoogle's Gemma 2: A Powerful, Efficient Language Model Google's Gemma family of language models, celebrated for efficiency and performance, has expanded with the arrival of Gemma 2. This latest release comprises two models: a 27-billion parameter ver
 The Next Wave of GenAI: Perspectives with Dr. Kirk Borne - Analytics VidhyaApr 22, 2025 am 11:21 AM
The Next Wave of GenAI: Perspectives with Dr. Kirk Borne - Analytics VidhyaApr 22, 2025 am 11:21 AMThis Leading with Data episode features Dr. Kirk Borne, a leading data scientist, astrophysicist, and TEDx speaker. A renowned expert in big data, AI, and machine learning, Dr. Borne offers invaluable insights into the current state and future traje
 AI For Runners And Athletes: We're Making Excellent ProgressApr 22, 2025 am 11:12 AM
AI For Runners And Athletes: We're Making Excellent ProgressApr 22, 2025 am 11:12 AMThere were some very insightful perspectives in this speech—background information about engineering that showed us why artificial intelligence is so good at supporting people’s physical exercise. I will outline a core idea from each contributor’s perspective to demonstrate three design aspects that are an important part of our exploration of the application of artificial intelligence in sports. Edge devices and raw personal data This idea about artificial intelligence actually contains two components—one related to where we place large language models and the other is related to the differences between our human language and the language that our vital signs “express” when measured in real time. Alexander Amini knows a lot about running and tennis, but he still
 Jamie Engstrom On Technology, Talent And Transformation At CaterpillarApr 22, 2025 am 11:10 AM
Jamie Engstrom On Technology, Talent And Transformation At CaterpillarApr 22, 2025 am 11:10 AMCaterpillar's Chief Information Officer and Senior Vice President of IT, Jamie Engstrom, leads a global team of over 2,200 IT professionals across 28 countries. With 26 years at Caterpillar, including four and a half years in her current role, Engst
 New Google Photos Update Makes Any Photo Pop With Ultra HDR QualityApr 22, 2025 am 11:09 AM
New Google Photos Update Makes Any Photo Pop With Ultra HDR QualityApr 22, 2025 am 11:09 AMGoogle Photos' New Ultra HDR Tool: A Quick Guide Enhance your photos with Google Photos' new Ultra HDR tool, transforming standard images into vibrant, high-dynamic-range masterpieces. Ideal for social media, this tool boosts the impact of any photo,
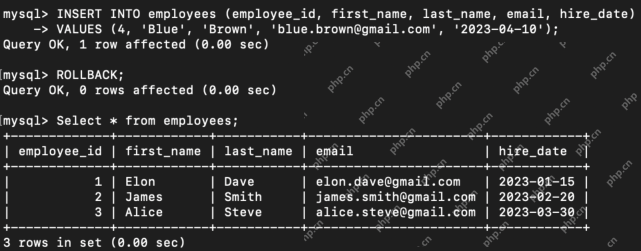 What are the TCL Commands in SQL? - Analytics VidhyaApr 22, 2025 am 11:07 AM
What are the TCL Commands in SQL? - Analytics VidhyaApr 22, 2025 am 11:07 AMIntroduction Transaction Control Language (TCL) commands are essential in SQL for managing changes made by Data Manipulation Language (DML) statements. These commands allow database administrators and users to control transaction processes, thereby
 How to Make Custom ChatGPT? - Analytics VidhyaApr 22, 2025 am 11:06 AM
How to Make Custom ChatGPT? - Analytics VidhyaApr 22, 2025 am 11:06 AMHarness the power of ChatGPT to create personalized AI assistants! This tutorial shows you how to build your own custom GPTs in five simple steps, even without coding skills. Key Features of Custom GPTs: Create personalized AI models for specific t
 Difference Between Method Overloading and OverridingApr 22, 2025 am 10:55 AM
Difference Between Method Overloading and OverridingApr 22, 2025 am 10:55 AMIntroduction Method overloading and overriding are core object-oriented programming (OOP) concepts crucial for writing flexible and efficient code, particularly in data-intensive fields like data science and AI. While similar in name, their mechanis


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SublimeText3 English version
Recommended: Win version, supports code prompts!

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

SublimeText3 Mac version
God-level code editing software (SublimeText3)

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

Atom editor mac version download
The most popular open source editor






