 Technology peripherals
Technology peripherals AI
AI Using Transformer as a general-purpose computer, it can also execute in-context learning algorithms. This research is very imaginative.
Using Transformer as a general-purpose computer, it can also execute in-context learning algorithms. This research is very imaginative.Using Transformer as a general-purpose computer, it can also execute in-context learning algorithms. This research is very imaginative.
Transformer has become a popular choice for various machine learning tasks and has achieved good results, so how else can it be used? Researchers with great imagination actually want to use it to design programmable computers!

##The authors of this paper are from Princeton University and the University of Wisconsin. The title is "Looped Transformers as Programmable Computers" and its purpose is I'm exploring how to use Transformer to implement a general-purpose computer.
Specifically, the authors propose a framework for using transformer networks as general-purpose computers by programming them with specific weights and placing them in loops. In this framework, the input sequence acts as a punch card, consisting of instructions and memory for data reading/writing.
The authors demonstrate that a constant number of encoder layers can simulate basic computational blocks. Using these building blocks, they simulated a small instruction set computer. This allowed them to map the iterative algorithm to a program that could be executed by a looped 13-layer transformer. They show how this transformer can simulate a basic calculator, a basic linear algebra library, and an in-context learning algorithm using backpropagation, guided by its inputs. This work highlights the versatility of attention mechanisms and demonstrates that even shallow transformers can perform full-blown general-purpose programs.
Paper OverviewTransformer (TF) has become a popular choice for various machine learning tasks, and it has achieved results on many problems in fields such as natural language processing and computer vision. state-of-the-art results. A key reason for Transformer's success is its ability to capture higher-order relationships and long-range dependencies through attention mechanisms. This allows TF to model contextual information and makes it more effective in tasks such as machine translation and language modeling, where Transformer consistently outperforms other methods.
Language models with hundreds of billions of parameters, such as GPT-3 (175B parameters) and PaLM (540B parameters), have achieved state-of-the-art performance on many natural language processing tasks. Interestingly, some of these large language models (LLMs) can also perform in-context learning (ICL), adapting and performing specific tasks on the fly based on a short prompt and some examples. The ICL capabilities of LLMs are available without having to train them, and allow these large models to efficiently perform new tasks without updating weights.
Surprisingly, through ICL, LLM can perform algorithmic tasks and inference, and [Nye et al. [2021], Wei et al. [2022c], Lewkowycz et al [2022], Wei et al. [2022b], Zhou et al. [2022]] and others have proven its feasibility. Work by [Zhou et al. [2022] ] and others demonstrates that LLM can successfully perform addition operations on unknown use cases when given a prompt with a multi-bit addition algorithm and some addition examples. These results show that LLM can perform pre-instructed commands on given inputs at inference time, based on algorithmic principles, as if interpreting natural language as code.
There is evidence that Transformer can simulate recursive links between Turing machines or Attention layers with sufficient depth [Pérez et al. [2021], Pérez et al. [2019], Wei et al. [2022a]]. This demonstrates the potential of Transformer networks to precisely follow the algorithmic instructions specified by the input. However, these constructs are relatively general and do not provide a deep understanding of how to create a Transformer capable of performing specific algorithmic tasks.
However, a more professional design allows TF to perform more advanced programs. For example, [Weiss et al. [2021]] designed a computational model and a programming language that map simple selection and aggregation commands to index input tokens. This language can be used to create a variety of interesting algorithms, such as token counting, sorting, creating histograms, and identifying Dyck-k languages. Programs written in Restricted Access Sequence Processing Language (RASP) can then be mapped into Transformer networks, whose size typically scales with the size of the program.
Another study demonstrated a method for selecting Transformer model weights for use as an optimization algorithm for dynamically learning linear regression models, performing implicit operations at inference time given training data as input. style training. These methods typically require a number of layers proportional to the number of iterations of the learning algorithm and are limited to a single loss function and ensemble of models.
The ability to program Transformer models to simulate the abstract computation of Turing machines, specialized commands for languages like RASP, and specific algorithms for ICL highlights the potential of Transformer networks as versatile programmable computers.
The author's research aims to explore this promising prospect and reveal how attention mechanisms can simulate general-purpose computers inspired by instruction set architectures.
Transformers as Programmable Computers
In this article, the authors show that Transformer networks can be made by hard-coding them with specific weights and placing them in a loop to simulate complex algorithms and programs. The authors did this by reverse-engineering Attention to simulate basic computational blocks, such as editing operations on input sequences, nonlinear functions, function calls, program counters, and conditional branches. The authors' paper demonstrates the importance of using a single loop or recursion to concatenate a Transformer's output sequence back to its input, thereby avoiding the need for a deep model.

##Paper address: https://arxiv.org/pdf/2301.13196.pdf
The author achieves this by designing a Transformer that can execute a program written in a general version of a single instruction, called SUBLEQ (A,B,C), that is, if less than or equal to zero, subtract and combine branch. SUBLEQ is a single-instruction language that defines a one-instruction set computer (OISC). SUBLEQ consists of 3 memory address operands. During execution, the value of memory address B is subtracted from the value of memory address A, and the result is stored in B. If the result of B is less than or equal to 0, jump to address C, otherwise continue executing the next instruction. But this instruction defines a general-purpose computer.
The author constructs an explicit Transformer that implements a SUBLEQ-like program. The author calls it FLEQ, a more flexible single instruction in the form

where f_m can be selected from a set of functions (matrix multiplication/nonlinear function/polynomial, etc.), which can be hard-coded into the network. The depth of a looping Transformer that can execute a FLEQ program does not depend on the depth of the program or the number of lines of code, but rather on the depth required to implement a single FLEQ instruction, which is constant. This is achieved by running the Transformer in a loop over the input sequence, similar to how a CPU operates.
The author uses this framework to demonstrate the ability to simulate various functions during reasoning, including a basic calculator, a basic linear algebra library (matrix transpose, multiplication, solution Inverse, power iteration) and ICL implementing backpropagation on implicitly fully connected networks. The input sequence or prompt acts like a punch card, containing the instructions that the Transformer needs to execute, while providing space for storing and handling variables used in the program. The Transformer networks used to perform these procedures all have a depth less than or equal to 13, and the weight matrices for all these models are provided. The following theorem summarizes the author's main findings:
Theorem 1: There exists a cyclic Transformer with less than 13 layers, which can simulate a general-purpose computer (Section 5 of the article), a basic calculator (Section 7 of the article), numerical linear algebra methods such as approximate matrix inversion and power iteration (Section 8 of the article), and ICL algorithms based on neural networks (such as SGD) (Section 9 of the article).

Figure 1: Schematic diagram of the loop Transformer architecture, in which the sequence storage command is input and read from / Memory for writing data and scratchpad for storing intermediate results. Inputs are processed by the network and outputs are used as new inputs, allowing the network to iteratively update implicit states and perform complex calculations.
The author's research emphasizes the flexibility of the Attention mechanism and the importance of a single loop, which makes it possible to design models that can simulate complex iterative algorithms and execute general programs. and further demonstrated the ability of the Transformer model to efficiently perform complex mathematical and algorithmic tasks. It is conceivable that modern Transformers, such as GPT-3, use similar internal subroutines when performing various tasks. To some extent, the capabilities of these model-specific techniques or algorithms can be enlightened when given contextual examples and explanations, similar to function calls. However, this assumption should be treated with caution, as the way the authors designed the structure bears no resemblance to how real-world language models are trained.
The authors hope that their study will encourage further research into the potential of attention mechanisms and the ability of language models to execute algorithmic instructions. The design proposed by the authors can help determine the minimum Transformer network size required to perform a specific algorithmic task. Additionally, the authors hope that their findings will help inspire the development of methods to enhance the ability to train language models by leveraging smaller, reverse-engineered Transformer networks to accomplish specific algorithmic tasks.
Building a Transformer module for general computing
To use the Transformer network to build a general computing framework, a specialized computing block is required. Assemble these blocks to create the desired final functionality. The following focuses on the various operations that the Transformer layer can perform. These operations will provide the basis for creating more complex routines and algorithms. These operations are designed to be interoperable with each other, leveraging Attention's ability to perform a variety of tasks, such as generating approximate permutation matrices and approximating general functions via sigmoid functions.

Figure 2: Three Transformer blocks used as building blocks for implementing a small instruction set computer schematic diagram. These blocks handle editing operations in the input sequence (such as moving or copying from one block to another), tracking the program counter, and performing program counter jumps when specified conditions are met.
Position encoding, program counter and data pointer
Transformer is usually required to perform iterative algorithms Or execute a series of commands. To achieve this, the author uses a program counter that loops through commands. The counter contains a code for the location where the next command is stored. Additionally, commands may have data pointers pointing to the data locations that the command needs to read and write. Both the program counter and the data pointer use the same positional encoding discussed in the previous paragraph.

The author's positional encoding scheme can also be used to point to specific data locations for reading or writing, which will be discussed below One section discusses. This is achieved by using the same binary vector as the position encoding for the program counter and data pointer. Additionally, this technique of pointing to specific data locations enables Transformers to efficiently read/write data during the execution of an algorithm or sequence of commands it was built to implement.
Read/write: copy data and instructions to or from the temporary register

# Figure 3: Schematic diagram of the read operation. The arrow shows the command block copied from the input portion assigned to the scratchpad command. An instruction is a set of pointers. Position codes and counters are used to track what content is copied where.
#The following lemma states that the command pointed to by the program counter or the data at the location specified in the current command can be copied to the scratchpad for further calculations. The location of the program counter is usually directly below the contents of the scratchpad, but can be changed arbitrarily. Keeping it in a specific position throughout the calculation helps keep the structure well organized.
The next lemma explains that a vector v stored in a scratchpad can be copied to a specified location in memory, as specified by the scratchpad itself. This allows data to be transferred from the scratchpad to a specific location in memory for further use or storage.

Figure 4: Schematic diagram of write operation. The arrow shows that the block of data is being copied from the scratchpad to the specified location in the input section allocated to memory. Positional encoding is used to track target locations and ensure data is written to the correct memory location.

##Conditional branch
In this part, the author implements a conditional branch instruction that evaluates a condition and sets the program counter to a specified location when the condition is true, or increments the program counter by 1 when the condition is false.
The form of the command is as follows: if mem[a]≤0, then go to i, where mem[a] is the value at a position in the memory part of the input sequence. This command has two parts: judging the inequality and modifying the program counter.
Simulating a Universal Single Instruction Set ComputerSUBLEQ Transformer
Mavaddat and Parhami back in 1988 It has been demonstrated in 2001 that there is an instruction and that any computer program can be converted into a program consisting of instantiations of this instruction. A variation of this instruction is SUBLEQ, which can access different registers or memory locations.
The way SUBLEQ works is simple. It accesses two registers in memory, gets the difference of their contents and stores it back to one of the registers, then if the result is negative it jumps to a different predefined line of code or continues with the next instruction of the current line . A computer built to execute SUBLEQ programs is called a single instruction set computer and is a general purpose computer, i.e. it is Turing complete if it has access to infinite memory.

The following describes the construction of a looping Transformer that can execute programs written with a specific instruction set. Transformer keeps track of lines of code, memory locations, and program counters, using the memory portion of the input as memory registers and the command portion as lines of code/instructions. The temporary register is used to record additions and pointers involved in each instruction, reading, writing, conditional branch operations, etc.

Figure 5: Graphical representation of the implementation of the OISC instruction block. The first two blocks transfer the data/commands to the scratchpad, the second and third perform the subtraction and store the result, and the last one performs the if goto command that completes the instruction.
FLEQ: A more flexible Attention-based computer
In this section, the author introduces FLEQ To introduce, it is a generalization of SUBLEQ, which defines a more flexible reduced instruction set computer. This implicit additional instruction set is based on a more advanced version of SUBLEQ and allows multiple functions to be implemented in the same Transformer network. The authors use the term FLEQ to refer to the instructions, language, and attention-based computers it defines.
FLEQ is designed to allow the implementation of complex algorithms such as matrix multiplication, square root calculations, activation functions, etc. by generating functions that are more general than simple subtraction.
Attention-based computer execution cycle. On each iteration of the loop Transformer, an instruction is fetched from the instruction set in the input based on the program counter. The instruction is then copied to the scratchpad. Depending on the function to be implemented, different function block locations are used to locally record the results of the function. Once the result is calculated, it is copied back to the specified memory location provided by the instruction.
The execution cycle is similar to that of a Single Instruction Set Computer (OISC) from the previous section, the main difference being that for each instruction, one can choose from a list of pre-selected functions. Functions take input as arbitrary arrays, such as matrices, vectors, and scalars.
The format of the input sequence. As shown in Figure 6, the input X of the loop Transformer can execute a program composed of a series of FLEQ instructions (X consists of three parts: temporary register, memory, and instructions).
Format of Transformer-based function block. Each function block is located in the lower left portion of input X, as shown in Figure 6.

Figure 6: Structure of input X for executing FLEQ command
Please refer to the original paper for more technical details and examples.
The above is the detailed content of Using Transformer as a general-purpose computer, it can also execute in-context learning algorithms. This research is very imaginative.. For more information, please follow other related articles on the PHP Chinese website!
 The Hidden Dangers Of AI Internal Deployment: Governance Gaps And Catastrophic RisksApr 28, 2025 am 11:12 AM
The Hidden Dangers Of AI Internal Deployment: Governance Gaps And Catastrophic RisksApr 28, 2025 am 11:12 AMThe unchecked internal deployment of advanced AI systems poses significant risks, according to a new report from Apollo Research. This lack of oversight, prevalent among major AI firms, allows for potential catastrophic outcomes, ranging from uncont
 Building The AI PolygraphApr 28, 2025 am 11:11 AM
Building The AI PolygraphApr 28, 2025 am 11:11 AMTraditional lie detectors are outdated. Relying on the pointer connected by the wristband, a lie detector that prints out the subject's vital signs and physical reactions is not accurate in identifying lies. This is why lie detection results are not usually adopted by the court, although it has led to many innocent people being jailed. In contrast, artificial intelligence is a powerful data engine, and its working principle is to observe all aspects. This means that scientists can apply artificial intelligence to applications seeking truth through a variety of ways. One approach is to analyze the vital sign responses of the person being interrogated like a lie detector, but with a more detailed and precise comparative analysis. Another approach is to use linguistic markup to analyze what people actually say and use logic and reasoning. As the saying goes, one lie breeds another lie, and eventually
 Is AI Cleared For Takeoff In The Aerospace Industry?Apr 28, 2025 am 11:10 AM
Is AI Cleared For Takeoff In The Aerospace Industry?Apr 28, 2025 am 11:10 AMThe aerospace industry, a pioneer of innovation, is leveraging AI to tackle its most intricate challenges. Modern aviation's increasing complexity necessitates AI's automation and real-time intelligence capabilities for enhanced safety, reduced oper
 Watching Beijing's Spring Robot RaceApr 28, 2025 am 11:09 AM
Watching Beijing's Spring Robot RaceApr 28, 2025 am 11:09 AMThe rapid development of robotics has brought us a fascinating case study. The N2 robot from Noetix weighs over 40 pounds and is 3 feet tall and is said to be able to backflip. Unitree's G1 robot weighs about twice the size of the N2 and is about 4 feet tall. There are also many smaller humanoid robots participating in the competition, and there is even a robot that is driven forward by a fan. Data interpretation The half marathon attracted more than 12,000 spectators, but only 21 humanoid robots participated. Although the government pointed out that the participating robots conducted "intensive training" before the competition, not all robots completed the entire competition. Champion - Tiangong Ult developed by Beijing Humanoid Robot Innovation Center
 The Mirror Trap: AI Ethics And The Collapse Of Human ImaginationApr 28, 2025 am 11:08 AM
The Mirror Trap: AI Ethics And The Collapse Of Human ImaginationApr 28, 2025 am 11:08 AMArtificial intelligence, in its current form, isn't truly intelligent; it's adept at mimicking and refining existing data. We're not creating artificial intelligence, but rather artificial inference—machines that process information, while humans su
 New Google Leak Reveals Handy Google Photos Feature UpdateApr 28, 2025 am 11:07 AM
New Google Leak Reveals Handy Google Photos Feature UpdateApr 28, 2025 am 11:07 AMA report found that an updated interface was hidden in the code for Google Photos Android version 7.26, and each time you view a photo, a row of newly detected face thumbnails are displayed at the bottom of the screen. The new facial thumbnails are missing name tags, so I suspect you need to click on them individually to see more information about each detected person. For now, this feature provides no information other than those people that Google Photos has found in your images. This feature is not available yet, so we don't know how Google will use it accurately. Google can use thumbnails to speed up finding more photos of selected people, or may be used for other purposes, such as selecting the individual to edit. Let's wait and see. As for now
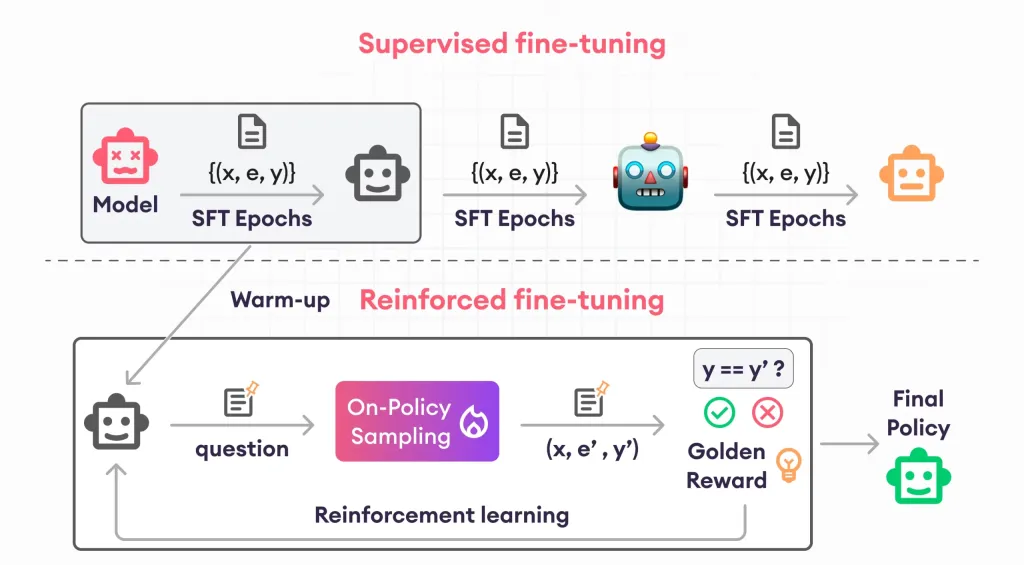 Guide to Reinforcement Finetuning - Analytics VidhyaApr 28, 2025 am 09:30 AM
Guide to Reinforcement Finetuning - Analytics VidhyaApr 28, 2025 am 09:30 AMReinforcement finetuning has shaken up AI development by teaching models to adjust based on human feedback. It blends supervised learning foundations with reward-based updates to make them safer, more accurate, and genuinely help
 Let's Dance: Structured Movement To Fine-Tune Our Human Neural NetsApr 27, 2025 am 11:09 AM
Let's Dance: Structured Movement To Fine-Tune Our Human Neural NetsApr 27, 2025 am 11:09 AMScientists have extensively studied human and simpler neural networks (like those in C. elegans) to understand their functionality. However, a crucial question arises: how do we adapt our own neural networks to work effectively alongside novel AI s


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SublimeText3 Chinese version
Chinese version, very easy to use

Safe Exam Browser
Safe Exam Browser is a secure browser environment for taking online exams securely. This software turns any computer into a secure workstation. It controls access to any utility and prevents students from using unauthorized resources.

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function

SublimeText3 Linux new version
SublimeText3 Linux latest version

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.






