Neurosymbolic Regression: Extracting Science from Data

Translator|Li Rui
Reviser|Sun Shujuan
The universe is noisy and chaotic, Complex enough to make predictions difficult. Human intelligence and intuition contribute to a basic understanding of some activities in the surrounding world, and are sufficient to have some basic understanding of individual events on macroscopic space and time scales from the limited perspective of individuals and small groups.
Natural philosophers in human prehistory and antiquity were mostly limited to common sense rationalization and guess testing. These methods have significant limitations, especially for things that are too large or complex, thus leading to the prevalence of superstitious or magical thinking.
This is not to disparage guessing and checking (which are the basis of modern scientific method), but to see that changes in human ability to investigate and understand are driven by the desire and tools to distill physical phenomena into mathematical expressions Caused.
This was especially evident after the Enlightenment led by Newton and other scientists, although there are traces of analytical reductionism in antiquity as well. The ability to move from observations to mathematical equations (and the predictions those equations make) is integral to scientific exploration and progress.
Deep learning is also fundamentally about learning transformations related to input-output observations, just as human scientists try to learn functional relationships between inputs and outputs in the form of mathematical expressions.
Of course, the difference is that the input-output relationship learned by deep neural networks (the result of the universal approximation theorem) consists of an uninterpretable "black box" of numerical parameters, mainly weights, biases and their connected node.
The universal approximation theorem states that a neural network that meets very relaxed criteria should be able to get very close to any well-behaved function. In practice, a neural network is a fragile and leaky abstraction that represents input-output relationships resulting from simple yet precise underlying equations.
Unless special attention is paid to training the model (or ensemble of models) to predict uncertainty, neural networks tend to perform very poorly when making predictions outside the distribution for which they were trained.
Deep learning predictions are also poor at making falsifiable predictions, i.e. out-of-the-box assumptions that form the basis of the scientific method. So while deep learning is a well-proven tool that's good at fitting data, its usefulness is limited in one of humanity's most important pursuits: exploring the universe around us through scientific methods.
Although deep learning has various shortcomings in human scientific endeavors, the huge fitting ability and numerous successes of deep learning in scientific disciplines cannot be ignored.
Modern science produces large amounts of data, the output of which cannot be observed by individuals (or even teams) and cannot be intuitively converted from noisy data into clear mathematical equations.
For this, you can turn to symbolic regression, an automated or semi-automated method of reducing data into equations.
The Current Gold Standard: Evolutionary Methods
Before getting into some exciting recent research on applying modern deep learning to symbolic regression, it is important to first understand the evolution of transforming data sets into equations The current state of the method. The most commonly mentioned symbolic regression package is Eureqa, which is based on genetic algorithms.
Eureqa was originally developed as a research project by Hod Lipson’s team at Cornell University and offered as proprietary software from Nutonian, which was later acquired by DataRobot Corporation. Eureqa has been integrated into the Datarobot platform, led by Michael Schmidt, co-author of Eureqa and CTO of Datarobot.
Eureqa and similar symbolic regression tools use genetic algorithms to simultaneously optimize systems of equations for accuracy and simplicity.
TuringBot is an alternative symbolic regression package based on simulated annealing. Simulated annealing is an optimization algorithm similar to metallurgical annealing used to change the physical properties of metals.
In simulated annealing, the "temperature" is lowered when selecting candidate solutions to the optimization problem, where higher temperatures correspond to acceptance of poorer solutions and are used to promote early exploration, enabling the search for the global optimal solution. merit and provide energy to escape local optima.
TuringBot is another symbolic regression package based on simulated annealing. Simulated annealing is an optimization algorithm similar to metallurgical annealing used to change the physical properties of metals.
In simulated annealing, the "temperature" is lowered when selecting candidate solutions to the optimization problem, where higher temperatures correspond to acceptance of poorer solutions and are used to promote early exploration, enabling the search for the global optimal solution. merit and provide energy to escape local optima.
TuringBot is a free version, but has significant limitations in data set size and complexity, and code modifications are not allowed.
While commercial symbolic regression software (especially Eureqa) provides an important baseline for comparison when developing new tools for symbolic regression, the role of closed source programs is limited.
Another open source alternative called PySR is released under the Apache 2.0 license and is led by Princeton University doctoral student Miles Cranmer and shares the optimization goals of accuracy and parsimony (simplicity), along with Eureqa and The combination method used by TuringBot.
In addition to providing a free and freely modifiable software library for performing symbolic regression, PySR is also interesting from a software perspective: it is written in Python but uses the Julia programming language as a fast backend.
While genetic algorithms are generally considered the current state-of-the-art for symbolic regression, the past few years have seen an exciting explosion of new symbolic regression strategies.
Many of these new developments leverage modern deep learning models, either as function approximation components in multi-step processes, or in an end-to-end manner based on large Transformer models, originally developed for natural language processing, And anything in between.
In addition to new symbolic regression tools based on deep learning, there is also a resurgence in probabilistic and statistical methods, especially Bayesian statistical methods.
Combined with modern computing power, a new generation of symbolic regression software is not only an interesting study in its own right, but also provides real utility and contributions to scientific disciplines including large data sets and comprehensive experiments.
Symbolic Regression with Deep Neural Networks as Function Approximators
Due to the universal approximation theorem described and studied by Cybenko and Hornik in the late 1980s/early 1990s, one can expect to have at least one Neural networks with nonlinear activation of hidden layers can approximate any well-behaved mathematical function.
In practice, deeper neural networks tend to achieve better performance on more complex problems. However, in principle, a hidden layer is needed to approximate various functions.
The physics-inspired AI Feynman algorithm uses the universal approximation theorem as part of a more complex puzzle.
AI Feynman (and its successor AI Feynman 2.0) was developed by physicists Silviu-Marian Udrescu and Max Tegmark (along with some colleagues). AI Feynman takes advantage of functional properties found in many physical equations, such as smoothness, symmetry, and compositionality, among other properties.
Neural networks function as function approximators, learning input-output transformation pairs represented in a data set and facilitating the study of these properties by generating synthetic data under the same functional transformations.
AI The functional properties Feynman uses to solve problems are common in physics equations, but cannot be applied arbitrarily to the space of all possible mathematical functions. However, they are still reasonable assumptions to look for in various functions that correspond to the real world.
Like the genetic algorithm and simulated annealing methods described previously, AI Feynman fits each new data set from scratch. There is no generalization or pre-training involved, and deep neural networks form only an orchestrated part of a larger, physically information-rich system.
AI Feynman symbolic regression did an excellent job of deciphering the 100 equations (or puzzles) in Feynman's physics lectures, but the lack of generalization meant that each new data set (corresponding to a new equation) required a large calculation budget.
A new set of deep learning strategies for symbolic regression leverage the highly successful family of Transformer models, originally introduced as natural language models by Vaswani et al. These new methods are not perfect, but using pre-training can save a lot of computational time during inference.
The first generation of symbolic regression based on natural language models
Given that the attention-based very large Transformer model has been widely used in computer vision, audio, reinforcement learning, recommendation systems and many other fields (in addition to text-based (original role in natural language processing) has achieved great success on a variety of tasks, so it is not surprising that the Transformer model will eventually be applied to symbolic regression as well.
While the realm of numeric input-output pairs to symbolic sequences requires some careful engineering, the sequence-based nature of mathematical expressions naturally lends itself to Transformer methods.
Crucially, using Transformer to generate mathematical expressions allowed them to leverage pre-training on the structure and numerical meaning of millions of automatically generated equations.
This also lays the foundation for improving the model through scaling up. Scaling is one of the main advantages of deep learning, where larger models and more data continue to improve model performance well beyond the classic statistical learning limitations of overfitting.
Scaling is the main advantage mentioned by Biggio et al. in their paper titled "Scalable Neural Symbolic Regression", which is called NSRTS. The NSRTS Transformer model uses a dedicated encoder to transform each input-output pair of the dataset into a latent space. The encoded latent space has a fixed size independent of the input size of the encoder.
NSRTS decoder constructs a sequence of tokens to represent an equation, conditioned on the encoded latent space and the symbols generated so far. Crucially, the decoder only outputs placeholders for numeric constants, but otherwise uses the same vocabulary as the pre-trained equations dataset.
NSRTS uses PyTorch and PyTorch Lightning and has a permissive open source MIT license.
After generating constant-free equations (called equation skeletons), NSRTS uses gradient descent to optimize the constants. This approach layers a general optimization algorithm on top of sequence generation, shared by the so-called “SymbolicGPT” developed simultaneously by Valipour et al.
Valipour et al. did not use an attention-based encoder as in the NSRTS method. Instead, a model based on the Stanford point cloud model PointNet is used to generate a fixed-dimensional feature set that is used by the Transformer decoder to generate equations. Like NSRT, Symbolic GPT uses BFGS to find the numerical constants of the equation skeleton generated by the Transformer decoder.
Second generation symbolic regression based on natural language models
While some recent articles describe the use of natural language processing (NLP) Transformers to achieve generalization and scalability of symbolic regression, The above models are not truly end-to-end as they do not estimate numerical constants.
This can be a serious flaw: imagine a model that generates equations with 1000 sinusoidal bases of different frequencies. Optimizing the coefficients of each term using BFGS will probably be a good fit for most input data sets, but in reality it's just a slow and roundabout way of performing Fourier analysis.
Just in the spring of 2022, the second generation Transformer-based symbolic regression model has been released on ArXiv by Vastl et al. on SymFormer, while another end-to-end Transformer was released by Kamienny and colleagues.
The important difference between these and previous Transformer-based symbolic regression models is that they predict numeric constants as well as symbolic mathematical sequences.
SymFormer uses a double-headed Transformer decoder to complete end-to-end symbol regression. One head produces mathematical symbols, and the second head learns the task of numerical regression, i.e. estimating numerical constants that appear in equations.
The end-to-end models of Kamienny and Vastl differ in details, such as the accuracy of numerical estimates, but the solutions of both groups still rely on subsequent optimization steps for refinement.
Even so, according to the authors, they have faster inference times and produce more accurate results than previous methods, produce better equation skeletons, and provide a good starting point for optimization steps and Estimate constant.
The Era of Symbolic Regression is Coming
In most cases, symbolic regression has been an elegant and computationally intensive machine learning method. Over the past decade, it has gained The attention is much lower than that of general deep learning.
This is partly due to the "use it and lose it" approach of genetic or probabilistic methods, which must start from scratch for each new data set, a characteristic that is inconsistent with intermediate applications from deep learning to symbolic regression. (such as AI Feynman) are the same.
Using the Transformer as an integral component in symbolic regression enables recent models to take advantage of large-scale pre-training, thereby reducing energy, time and computational hardware requirements at inference time.
This trend has been extended further with new models that can estimate numerical constants and predict mathematical symbols, enabling faster inference and greater accuracy.
The task of generating symbolic expressions, which in turn can be used to generate testable hypotheses, is a very human task and is at the heart of science. Automated methods of symbolic regression have continued to make interesting technical advances over the past two decades, but the real test is whether they are useful to researchers doing real science.
Symbolic regression is starting to produce more and more publishable scientific results beyond technical demonstrations. A Bayesian symbolic regression approach yields a new mathematical model for predicting cell division.
Another research team used a sparse regression model to generate reasonable equations for ocean turbulence, paving the way for improved multiscale climate models.
A project combining graph neural networks and symbolic regression with Eureqa’s genetic algorithm generalizes expressions describing many-body gravity and derives a new equation describing the distribution of dark matter from conventional simulators .
Future development of symbolic regression algorithm
Symbolic regression is becoming a powerful tool in the scientist's toolbox. The generalization and scalability of Transformer-based methods are still hot topics and have not yet penetrated into general scientific practice. As more researchers adapt and improve the model, it promises to further advance scientific discoveries.
Many of these projects are conducted under open source licenses, so you can expect them to have an impact within a few years, and their application may be wider than proprietary software such as Eureqa and TuringBot.
Symbolic regression is a natural complement to the output of deep learning models, which are often mysterious and difficult to interpret, whereas output that is more understandable in mathematical language can help generate new testable hypotheses and Driving intuitive leaps.
These characteristics and the straightforward capabilities of the latest generation of symbolic regression algorithms promise to provide greater opportunities for moments of significant discovery.
The above is the detailed content of Neurosymbolic Regression: Extracting Science from Data. For more information, please follow other related articles on the PHP Chinese website!
 Tesla's Robovan Was The Hidden Gem In 2024's Robotaxi TeaserApr 22, 2025 am 11:48 AM
Tesla's Robovan Was The Hidden Gem In 2024's Robotaxi TeaserApr 22, 2025 am 11:48 AMSince 2008, I've championed the shared-ride van—initially dubbed the "robotjitney," later the "vansit"—as the future of urban transportation. I foresee these vehicles as the 21st century's next-generation transit solution, surpas
 Sam's Club Bets On AI To Eliminate Receipt Checks And Enhance RetailApr 22, 2025 am 11:29 AM
Sam's Club Bets On AI To Eliminate Receipt Checks And Enhance RetailApr 22, 2025 am 11:29 AMRevolutionizing the Checkout Experience Sam's Club's innovative "Just Go" system builds on its existing AI-powered "Scan & Go" technology, allowing members to scan purchases via the Sam's Club app during their shopping trip.
 Nvidia's AI Omniverse Expands At GTC 2025Apr 22, 2025 am 11:28 AM
Nvidia's AI Omniverse Expands At GTC 2025Apr 22, 2025 am 11:28 AMNvidia's Enhanced Predictability and New Product Lineup at GTC 2025 Nvidia, a key player in AI infrastructure, is focusing on increased predictability for its clients. This involves consistent product delivery, meeting performance expectations, and
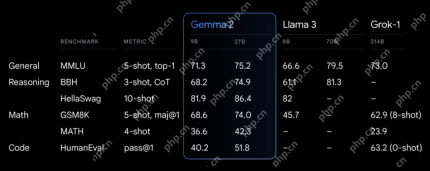 Exploring the Capabilities of Google's Gemma 2 ModelsApr 22, 2025 am 11:26 AM
Exploring the Capabilities of Google's Gemma 2 ModelsApr 22, 2025 am 11:26 AMGoogle's Gemma 2: A Powerful, Efficient Language Model Google's Gemma family of language models, celebrated for efficiency and performance, has expanded with the arrival of Gemma 2. This latest release comprises two models: a 27-billion parameter ver
 The Next Wave of GenAI: Perspectives with Dr. Kirk Borne - Analytics VidhyaApr 22, 2025 am 11:21 AM
The Next Wave of GenAI: Perspectives with Dr. Kirk Borne - Analytics VidhyaApr 22, 2025 am 11:21 AMThis Leading with Data episode features Dr. Kirk Borne, a leading data scientist, astrophysicist, and TEDx speaker. A renowned expert in big data, AI, and machine learning, Dr. Borne offers invaluable insights into the current state and future traje
 AI For Runners And Athletes: We're Making Excellent ProgressApr 22, 2025 am 11:12 AM
AI For Runners And Athletes: We're Making Excellent ProgressApr 22, 2025 am 11:12 AMThere were some very insightful perspectives in this speech—background information about engineering that showed us why artificial intelligence is so good at supporting people’s physical exercise. I will outline a core idea from each contributor’s perspective to demonstrate three design aspects that are an important part of our exploration of the application of artificial intelligence in sports. Edge devices and raw personal data This idea about artificial intelligence actually contains two components—one related to where we place large language models and the other is related to the differences between our human language and the language that our vital signs “express” when measured in real time. Alexander Amini knows a lot about running and tennis, but he still
 Jamie Engstrom On Technology, Talent And Transformation At CaterpillarApr 22, 2025 am 11:10 AM
Jamie Engstrom On Technology, Talent And Transformation At CaterpillarApr 22, 2025 am 11:10 AMCaterpillar's Chief Information Officer and Senior Vice President of IT, Jamie Engstrom, leads a global team of over 2,200 IT professionals across 28 countries. With 26 years at Caterpillar, including four and a half years in her current role, Engst
 New Google Photos Update Makes Any Photo Pop With Ultra HDR QualityApr 22, 2025 am 11:09 AM
New Google Photos Update Makes Any Photo Pop With Ultra HDR QualityApr 22, 2025 am 11:09 AMGoogle Photos' New Ultra HDR Tool: A Quick Guide Enhance your photos with Google Photos' new Ultra HDR tool, transforming standard images into vibrant, high-dynamic-range masterpieces. Ideal for social media, this tool boosts the impact of any photo,


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

Dreamweaver Mac version
Visual web development tools

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software






