How to find prime numbers in javascript

How to find prime numbers: 1. Traverse all natural numbers in the range 1~n and divide by n. If the remainder is 0, it means that the number n is not a prime number, otherwise it is a prime number. The syntax "for(i=2 ;i

The operating environment of this tutorial: windows7 system, javascript version 1.8.5, Dell G3 computer.

The concept of prime numbers

Prime numbers are also called prime numbers. A prime number refers to a number that is not divisible by other natural numbers except 1 and itself among the natural numbers greater than 1. .

Prime numbers within 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71 , 73, 79, 83, 89, 97, 25 in total.

Four ways to determine prime numbers using JavaScript

1. Prime numbers can only be divisible by 1 and itself

Prime numbers can only It is divisible by 1 and itself, so all natural numbers in the open interval (1, n) are traversed and divided by n. If there is an integer division, that is, the remainder is 0, it means that the number n is not a prime number, otherwise it is a prime number.

function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 2; i <p>But the complexity of this algorithm is O(n)</p><h3 id="strong-The-range-of-square-roots-of-prime-numbers-strong"><strong>2. The range of square roots of prime numbers</strong></h3><p>Assuming n is not a prime number, then n except It can be divided not only by 1 and n, but also by i and j, that is, n / i = j...0, for example, 15 is not a prime number, 15 / 3 = 5, for example, 35 is not a prime number, 35 / 5 = 7, this When i and j must be in (1, Math.sqrt(n)] and [Math.sqrt(n), n) respectively, for example, Math.sqrt(15) ≈ 3.8, then 3 is in (1, 3.8], 5 is in [3.8, 15). For example, Math.sqrt(4) = 2, then 2 is in (1,2] and also in [2,4). </p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 2; i <p>The complexity of the algorithm at this time is O(sqrt(n))</p><h3 id="strong-The-prime-number-cannot-be-any-other-even-number-other-than-strong"><strong>3. The prime number cannot be any other even number other than 2</strong></h3><p>Except 2, All even numbers are not prime numbers</p><p><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/image/644/149/762/1663645614907138.png?x-oss-process=image/resize,p_40" class="lazy" title="1663645614907138.png" alt="How to find prime numbers in javascript"></p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  if (n % 2 === 0) {
    return false;
  }
 
  for (let i = 3; i <p>n in the for loop can only be the light blue part of the picture above. </p><p> Therefore, the above algorithm reduces the loop by half, and the time complexity is O(sqrt(n) / 2) </p><p>It should be noted that the code of this algorithm cannot be n % 2 == The judgment condition of = 0 is added to the loop. There is a loophole in the following code. </p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 3; i <p>At this time, 4, 6, and 8 will all be judged as prime numbers. </p><p>The reason for the vulnerability is that the loop condition i </p><p>This algorithm can only ensure that the n value of n when the loop condition i = i^2 = 9. </p><h3 id="strong-Prime-numbers-greater-than-or-equal-to-must-be-adjacent-to-multiples-of-strong"><strong>4. Prime numbers greater than or equal to 5 must be adjacent to multiples of 6</strong></h3><p>Prime numbers greater than or equal to 5 must be adjacent to multiples of 6</p><p> (Note that this sentence is not equivalent to: Numbers adjacent to <span style="text-decoration:line-through;"> and multiples of 6 must be prime numbers </span> greater than 5. This conclusion is not true.) </p><p><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/image/674/593/865/1663645632699688.png?x-oss-process=image/resize,p_40" class="lazy" title="166364562667908How to find prime numbers in javascript" alt="How to find prime numbers in javascript"></p><p>As shown in the picture above, numbers greater than or equal to 5 are divided into: 6y-1, 6y, 6y 1, 6y 2, 6y 3, 6y 4 (y>=1)</p><p>Among them, 6y, 6y 2 , 6y 3, and 6y 4 cannot be prime numbers. Only 6y-1 and 6y 1<strong><span   style="max-width:90%">may</span></strong> are prime numbers. </p><p>In addition, 6y-1 (y>=1) and 6y 5 (y>=0) are equivalent. </p><p>So, we can directly exclude the numbers where n is not 6y-1 (or 6y 5) and 6y 1. The elimination method is, </p><pre class='brush:php;toolbar:false;'>  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }

Next, we need to eliminate 6y-1 (or The non-prime numbers in 6y 5) and 6y 1,

  for (let i = 5; i <= Math.sqrt(n); i += 6) {
    if (n % i === 0 || n % (i + 2) === 0) {
      return false;
    }
  }

There may be two things you are confused about here:

• Why is the increment of i in the for loop 6
• Why is the condition for prime number determination in the for loop n % i === 0 || n % (i 2) === 0

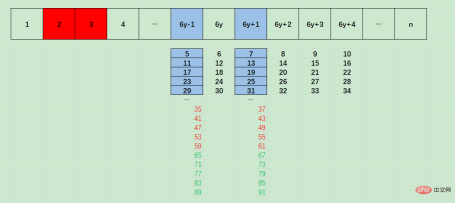
Looking at the above diagram, we can find that 6y-1 is an arithmetic sequence with a base of 5 and a difference of 6, that is, 5 6x:

• 对于 5 + 6x 而言，如果x为5的倍数（5 * z），则5 + 6x = 5 + 6 * 5 * z = 5 *（1+6z）,则此时5 + 6x可以被5整除。
• 5 + 6x 还可以转化为 5 + 6 + 6 * (x-1) = 11 + 6(x-1)，则只要x-1为11的倍数，则5 + 6x可以被11整除，
• 5 + 6x 还可以转化为 5 + 12 + 6 * (x-2) = 17 + 6(x-2)，则只要x-2为17的倍数，则5 + 6x可以被17整除
• ......

6y+1，是基数为7，差值为6的等差数列，即 7 + 6x :

• 对于 7 + 6x 而言，如果x为7的倍数（7 * z），则7 + 6x = 7 + 6 * 7 * z = 7 *（1+6z）,则此时7 + 6x可以被7整除。
• 7 + 6x 还可以转化为 7 + 6 + 6 * (x-1) = 13 + 6(x-1)，则只要x-1为13的倍数，则7 + 6x可以被13整除，
• 7 + 6x 还可以转化为 7 + 12 + 6 * (x-2) = 19 + 6(x-2)，则只要x-2为19的倍数，则7 + 6x可以被19整除，
• ......

所以6y-1和6y+1可能整除的数自增量为6，这是for循环i自增为啥是 6的原因

且6y-1和6y+1的整除数基数为5和7，相差为2，这是for循环中素数判定的条件为啥是 n % i === 0 || n % (i+2) === 0的原因

function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }
 
  for (let i = 5; i <p>此时时间复杂度为 O（sqrt(n) / 3） <br></p><p>【相关推荐：<a href="https://www.php.cn/course/list/17.html" target="_blank" textvalue="javascript视频教程">javascript视频教程</a>、<a href="https://www.php.cn/course/list/91.html" target="_blank" textvalue="编程基础视频">编程基础视频</a>】</p>

The above is the detailed content of How to find prime numbers in javascript. For more information, please follow other related articles on the PHP Chinese website!