Learn about trees and binary trees in three minutes

In the computer field, the [folders] we deal with every day and the data we store in the database are all typical applications of trees. Today we are going to learn about the more theoretical definitions of trees and binary trees and some of their attributes and characteristics.

Tree

From the above examples in real life, we can see that the tree structure can summarize some of its characteristics.

Tree (Tree) is a finite set of N (N>0) nodes. It is either an empty tree (N=0) or a non-empty tree T.

In this definition, we need to clarify two issues: First, the tree must have nodes, and second, according to the number of nodes, it can be divided into two types: empty trees and non-empty trees. But this is just the most basic definition, it has some properties.

There is and is only one node called the root.

In other words, this tree must expand from a certain node, which is the same as the root of the tree. From it begin to branch outwards.

Except for the root node, the remaining nodes can be divided into m ( m > 0 ) disjoint finite sets T1, T2..., Tm, each of which is itself a tree, and Subtree called the root (SubTree)

This paragraph may not be easy to understand. In fact, to put it bluntly, each node has only one superior node and cannot have multiple superior nodes. In the same way, there cannot be any connection between horizontal nodes, but it can have multiple subordinate nodes.

Regarding the definition of tree, we can look at the picture below.

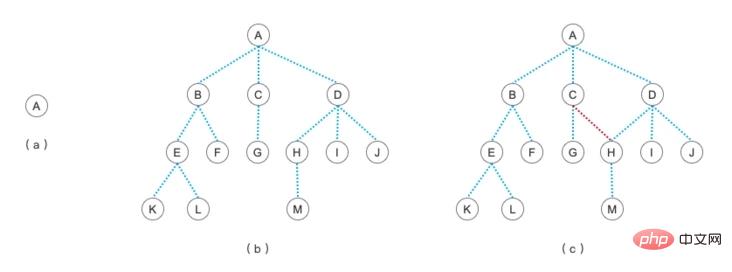
The above picture simply lists what standard trees and non-standard trees look like. Among them:

• (a) is a tree with only one root node. As long as there is one node, it can be called a tree structure

• (b) is a standard tree structure

• (c). Note that there is a connecting line between its C and H nodes. This is not a tree. A node that can only have one superior node is called a tree. This is actually what we will learn in the future [Picture]

Related terms for trees

Compared to the pushing (pushing) and popping of the stack, and the enqueuing and dequeuing of the queue, the related terms of the tree are much more complicated. No matter what, you have to remember these terms first, otherwise the terminology used in what will be discussed later will only make you more confused. But it doesn’t matter if we can’t remember it for the moment. We can have a rough impression first, and then come back to review it when we encounter it later in the learning process. This way the impression will be more profound.

• Node: A node may contain a set of data, or a branch pointing to other nodes. It can be regarded as the place where the branches branch. (b) In the figure A, B, C, D, E, etc. are all the degrees of nodes

• : The number of subtrees owned by a node is called the degree of the node, which is actually its subordinates. The number of child nodes is the degree. In the figure (b), the degree of node C is 1 and the degree of node D is 3.

• The degree of the tree: the degree of each node in the tree The maximum value of a node's degree is the degree with the most child nodes. This is the degree of the tree. (b) The degree of the tree in the figure is 3

• Leaves: Degree A node is 0, that is, a node without child nodes. (b) K, L, F, G, M, I, J in the figure are the leaf nodes of this tree

• Parents and children: The child nodes of a node are its children; for these child nodes, the current node is its parents. (b) In the figure, the child of D is H , I, J, and the parents of H, I, J are the D

• level: counting from the root node, the root node is the first level, and the root's children are the second level. , and so on, (b) the level of G node in the figure is 3, (a) all levels of the figure are only 1

• The depth (height) of the tree: the current tree The maximum level of the tree, obviously, (b) the depth of the graph is 4

• brothers, ancestors and descendants: brother nodes are the parents of these nodes are the same node; ancestors Nodes are all nodes passing through on the way from the root node to a specified node; descendants are all nodes on the way from a certain node to the target node. (b) In the figure, E and F are brothers, E’s ancestors are A and B, and E’s descendants are K or L

• cousins: all on the same level Nodes with different parents are cousins. Also in Figure (b), G’s cousins ​​are E and F, and H, I, and J are also its cousins

Binary tree

After we have a certain understanding of the concept of tree, we will further learn another concept, also in data structure and algorithm The most important form of tree: the binary tree.

Generally speaking, the shape of the tree can be ever-changing. For example, one node may have 3 child nodes, while another node may have 300 child nodes. Such a tree without any rules will actually be very troublesome to operate, and the definition of a binary tree is much simpler. In addition to the properties of a tree, it also has one more content: each node of a binary tree has at most two child nodes. , that is to say, the degree of the entire binary tree must be 2, and the degree of all nodes will not exceed 2. As for why binary trees are easy to operate, we will explain in detail in the properties of binary trees in the next section. All tree structures can be converted into binary trees through certain regular deformations.

We also use a diagram to show what a binary tree is.

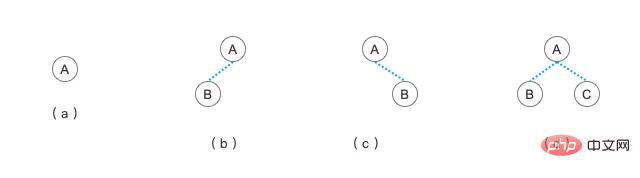
In a binary tree, the left child node and its descendants can be regarded as the left subtree of the current node. The right node and its descendant nodes can also be regarded as the right subtree of the current node. According to the child nodes of the node, there are several binary tree forms as shown in the above figure.

• (a) A tree is a tree with only one node, it can also be said to be a binary tree with only one node

• (b ) The tree is a binary tree with only one left node

• (c) The tree is a binary tree with only one right node

• (d ) tree is a binary tree with two left and right nodes

Properties of binary trees

Property 1: At the i-th level of the binary tree There are at most 2i-1 nodes (i >= 1)

Property 2: A binary tree with depth k has at most 2k - 1 nodes (k >= 1)

Property 3: For any binary tree T, if the number of terminal nodes is n0 and the number of nodes with degree 2 is n2, then n0 = n2 1

Property 4: A complete binary tree with n nodes The depth of is log2n 1

Property 5: If the nodes of a complete binary tree with n nodes (its depth is log2n 1) are numbered in layer order (from the first layer to the log2n 1 layer , each layer from left to right), then for any node i (1

1. If i = 1, then the node i is the root of the binary tree and has no parents; if i > 1, then its parent is node i / 2
2. If 2i > n, then node i has no left child (node ​​i is a leaf node point); otherwise its left child is node 2i
3. If 2i 1 > n, then node i has no right child; otherwise its right child is node 2i 1

We will not go into details about the mathematical proofs of the above five properties of binary trees. After all, the purpose of this series of articles is to let everyone learn the essence of data structures and algorithms through simple examples, rather than simply and crudely using them directly. Mathematical formulas are used to derive proofs, so we can just count them directly on the picture.

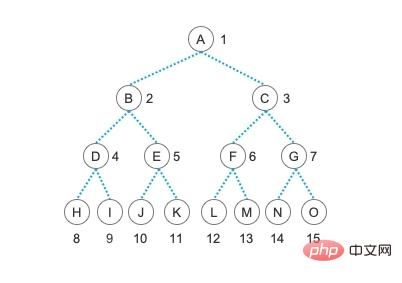
• For property 1, according to the formula, our current binary tree can only have a maximum of 23-1 nodes on the third level. , that is, 4 nodes. There can only be at most 24-1 on the 4th layer, that is, 23 = 8 nodes

• For property 2, the depth of the tree in the current picture is 4, that is, That is, there are at most 24 - 1 = 15 nodes

• For property 3, we first count the number of nodes with degree 2. In this figure, the nodes with degree 2 There are 7 points, namely A, B, C, D, E, F, G. The nodes on the fourth level have no child nodes, that is to say, they are all 0 degrees, also called terminal nodes. points (leaf nodes), the number of these nodes is 8 in total. Now n2 = 7, according to the property formula we can get n0 = n2 1 = 7 1 = 8

• The number of nodes in the graph is 15, and applying the formula of property 4 we can get Out of log2n 1 = log215 1 = 3.91 (rounded down) 1 = 3 1 = 4, the depth of the current tree is 4, and property 4 and property 2 can be regarded as complementary

• For property 5, please pay attention to the number on the edge of each node. We will choose the E node as an example. The E node is currently 5, so its parents are 5 / 2 = 2 (rounded down); the left child of E is 2i, which is 2*5=10, and the right child of E is 2i 1, which is 2 *5 1 = 11; The definition of property 5 is more abstract, and it uses leaf nodes to illustrate, which is aimed at the entire binary tree, but in fact the meaning is the same as what we explain here, you can Verify it with other nodes. Property 5 is very important for the use of sequential structures to store binary trees that we will talk about later!

Please be sure to master and remember these five properties of binary trees and their meanings, because in the subsequent study, whether it is the order of binary trees, chain storage structures, or the traversal of binary trees , are likely to be exposed to the contents of the five properties above. It can be said that they are the most basic soul in binary tree learning.

Forest

Finally, let’s briefly understand what “forest” is. Multiple trees put together form a "forest". Just like the explanation diagram of the binary tree above, (a) (b) (c) (d) are put together and viewed as a whole, it is a "forest", and in this "forest" there are (a) (b) (c) (d) these four trees.

There is no connection between the trees in the forest. If we want to operate or traverse a forest, we often convert the forest into a tree. The specific algorithms and steps are not the focus of our study, so everyone can understand it. Students who want to study in depth can search for relevant content or consult relevant textbooks.

Summary

Going from the stack and queue to the back of the tree, do you suddenly feel that you have taken a big step? A little confused? It doesn't matter, today's content is actually some basic theoretical content. If you can understand it, understand it. If you can't understand it, continue studying and then come back to look at today's concepts.

Learning does not involve constantly repeating the process of progress. Of course, everything must still be based on the foundation. After you understand the data structure of trees and some simple traversal algorithms, come back to understand these concepts in depth and memorize them. I believe that tree-related questions in general interviews will be out of the question. Let’s work hard together!

Recommended learning: php video tutorial

The above is the detailed content of Learn about trees and binary trees in three minutes. For more information, please follow other related articles on the PHP Chinese website!