How to implement sorting and search algorithms in JS

The content of this article is to introduce how to use JS to implement sorting and search algorithms. It has certain reference value. Friends in need can refer to it. I hope it will be helpful to you.

1. Preparation

Before getting into the topic, prepare a few basic functions

(1) Exchange two elements of the array

function swap(arr, sourceIndex, targetIndex) {
  let temp = arr[sourceIndex];
  arr[sourceIndex] = arr[targetIndex];
  arr[targetIndex] = temp;
}

(2) Quickly generate an array of 0~N

function createArr(length) {
  return Array.from({length}, (_, i) => i);
}

(3) Shuffle function

The shuffling function can quickly disrupt the array. Common uses include switching the order of music playback

function shuffle(arr) {
  for (let i = 0; i <h2><strong>2. Sorting</strong></h2><p>Common sorting algorithms can Divided into two major categories: </p>

• Comparison sorting: Determine the relative order between elements through comparison, because its time complexity cannot exceed O(nlogn), so it is also called non-linear time comparison sorting
• Non-comparison sorting: It does not determine the relative order between elements through comparison, it can break through the time lower bound of comparison-based sorting , runs in linear time, so it is also called linear time non-comparison sorting

In this article, there are only several sorting methods for comparison sorting Introduction to learning

2.1 Bubble sort

Bubble sort is the simplest of all sorting algorithms and is usually the introductory method for us to learn sorting. However, from a running time perspective, bubble sort is the worst sorting method.

Core: Compare any two adjacent items, and if the first is greater than the second, swap them. The items are moved up into the correct order, as if bubbles were rising to the surface, hence the name bubble sort

Gif:

Note: The first level traverses to find the maximum value of the remaining elements, and reaches the specified position [bubbles out the maximum value in turn]

Code:

function bubbleSort(arr) {
  const len = arr.length;
  for (let i = 0; i  arr[j + 1]) { // 比较相邻元素
        swap(arr, j, j + 1);
      }
    }
  }
  return arr;
}

2.2 Selection sort

Selection sort is an in-place comparison sorting algorithm.

Core: First find the smallest element in the unsorted sequence, store it at the starting position of the sorted sequence, then continue to find the smallest element from the remaining unsorted elements, and then put it into the sorted sequence. the end of. And so on until all elements are sorted

Gif:

Note: First Layer traversal finds the index of the minimum value of the remaining elements, and then exchanges the current position and the minimum index value [find the minimum value in turn]

Code:

function selectionSort(arr) {
  const len = arr.length;
  let minIndex;
  for (let i = 0; i  arr[j]) {
        minIndex = j; // 寻找最小值对应的索引
      }
    }
    if (minIndex === i) continue;
    swap(arr, minIndex, i);
  }
  return arr;
}

2.3 Insertion sort

The comparison order of insertion sort is different from bubble sort and selection sort. The comparison order of insertion sort is forward comparison of the current item.

Core: By constructing an ordered sequence, for unsorted data, scan from back to front in the sorted sequence, find the corresponding position and insert

GIF:

Note: Starting from the second item, compare forward in order to ensure that the previous sequence of the current item is in order

Code:

function insertionSort(arr) {
  const len = arr.length;
  let current, pointer;
  for (let i = 1; i = 0 && current <h3><strong>2.4 Merge sort</strong></h3><p> Compared with the above three sorting algorithms, merge sort and quick sort are more practical in practice is more feasible (in the fourth section we will compare these sorting algorithms through practical complexity) </p><blockquote>
<code>JavaScript</code>'s <code>Array</code> class defines a # The ##sort<code> function (</code>Array.prototype.sort<code>) is used to sort the </code>JavaScript<code> array. </code>ECMAScript<code> does not define which sorting algorithm is used, so browser manufacturers can implement the algorithm themselves. For example, </code>Mozilla Firefox<code> uses </code>mergesort<strong> as an implementation of </strong>Array.prototype.sort<code>, while </code>Chrome<code> uses a </code>quicksort Variation of <strong></strong>
</blockquote><p> Merge sort is a <strong>divide-and-conquer algorithm<code>. The idea is to split the original array into smaller arrays until each small array has only one position, and then merge the small arrays into larger arrays until there is only one sorted large array. Therefore, you need to use </code>recursion<code></code></strong></p>##Core: merge sort, split into left and right arrays, sort them separately and then merge<p><strong></strong></p>GIF:<p style="text-align: left;"><strong></strong></p><p style="text-align: center;"></p><p><strong>注意：递归中最小的左右数组比较为单个元素的数组，因此在较上层多个元素对比时，左右两个数组一定是顺序的</strong></p><p><strong>代码：</strong></p><pre class="brush:php;toolbar:false">function mergeSort(arr) {
  const len = arr.length;

  if (len  right[0]) {
      ret.push(right.shift());
    } else {
      ret.push(left.shift());
    }
  }

  while (left.length) {
    ret.push(left.shift());
  }
  while (right.length) {
    ret.push(right.shift());
  }

  return ret;
}

2.5 快速排序

快速排序也许是最常用的排序算法了。它的复杂度为O(nlogn)，且它的性能通常比其他的复 杂度为O(nlogn)的排序算法要好。和归并排序一样，快速排序也使用分治的方法，将原始数组分为较小的数组

核心：分治算法，以参考值为界限，将比它小的和大的值拆开

动图：

注意：每一次遍历筛选出比基准点小的值

代码：

function quickSort(arr, left = 0, right = arr.length - 1) {
  // left和right默认为数组首尾
  if (left <h2><strong>三、搜索算法</strong></h2><h3><strong>3.1 顺序搜索</strong></h3><p>顺序或线性搜索是最基本的搜索算法。它的机制是，将每一个数据结构中的元素和我们要找的元素做比较。<strong>顺序搜索是最低效的一种搜索算法。</strong></p><pre class="brush:php;toolbar:false">function findItem(item, arr) {
  for (let i = 0; i <h3><strong>3.2 二分搜索</strong></h3><p>二分搜索要求被搜索的数据结构已排序。以下是该算法遵循的步骤：</p><ol>
<li>选择数组的中间值</li>
<li>如果选中值是待搜索值，那么算法执行完毕</li>
<li>如果待搜索值比选中值要小，则返回步骤1在选中值左边的子数组中寻找</li>
<li>如果待搜索值比选中值要大，则返回步骤1在选中值右边的子数组中寻找</li>
</ol><pre class="brush:php;toolbar:false">function binarySearch(item, arr) {
  arr = quickSort(arr); // 排序

  let low = 0;
  let high = arr.length - 1;
  let mid;

  while (low  item) {
      high = mid - 1;
    } else {
      return mid;
    }
  }
  return -1;
}

四、算法复杂度

4.1 理解大O表示法

大O表示法用于描述算法的性能和复杂程度。分析算法时，时常遇到一下几类函数

（1）O(1)

function increment(num){
    return ++num;
}

执行时间和参数无关。因此说，上述函数的复杂度是O(1)(常数)

（2）O(n)

以顺序搜索函数为例，查找元素需要遍历整个数组，直到找到该元素停止。函数执行的总开销取决于数组元素的个数(数组大小)，而且也和搜索的值有关。但是函数复杂度取决于最坏的情况：如果数组大小是10，开销就是10；如果数组大小是1000，开销就是1000。这种函数的时间复杂度是O(n)，n是(输入)数组的大小

（3）O(n2)

以冒泡排序为例，在未优化的情况下，每次排序均需进行n*n次执行。时间复杂度为O(n2)

时间复杂度O(n)的代码只有一层循环，而O(n2)的代码有双层嵌套循环。如 果算法有三层遍历数组的嵌套循环，它的时间复杂度很可能就是O(n3)

4.2 时间复杂度比较

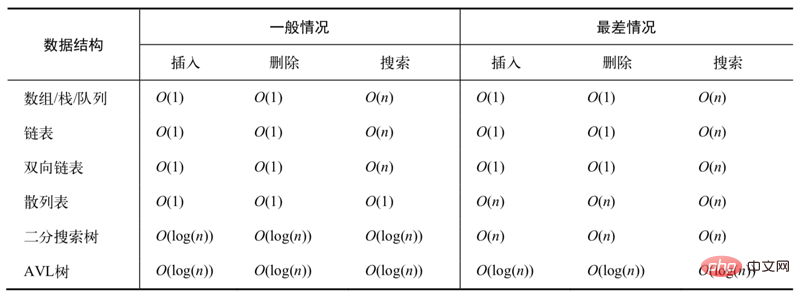
（1）常用数据结构时间复杂度

（2）排序算法时间复杂度

相关视频教程推荐：《JavaScript教程》

以上就是本篇文章的全部内容，希望能对大家的学习有所帮助。更多精彩内容大家可以关注php中文网相关教程栏目！！！

The above is the detailed content of How to implement sorting and search algorithms in JS. For more information, please follow other related articles on the PHP Chinese website!