Introduction to methods of implementing recursive algorithms in JavaScript

This article brings you an introduction to the method of implementing recursive algorithms in JavaScript. It has certain reference value. Friends in need can refer to it. I hope it will be helpful to you.

Let’s take a look at the definition first. A recursive algorithm converts a problem into sub-problems of the same type that are reduced in size, and each sub-problem is solved using the same algorithm. Generally speaking, a recursive algorithm is a function that calls itself to solve its subproblems.

Characteristics of recursive algorithms:

1. calls itself during the function process.
2. In the recursive process, there must be a clear condition to judge the end of the recursion, that is, the recursive exit.
3. The recursive algorithm is simple but inefficient and is usually not recommended as a recommended algorithm.

The above are explanations from Baidu Encyclopedia, and they are very clear. Please consider them carefully with examples.

　Factorial

　Problem description: n! = n*(n-1)*...2*1

Code implementation:

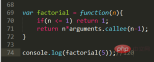
When we get the problem, we can first reduce the scale to similar sub-problems according to the definition. For example, n! is equal to n* (n-1)!, then (n-1)! = (n-1)*(n-2)!. Push down in this order until the exit of if. arguments.callee is used here to prevent tight coupling of function names. Here it is equivalent to factorial(n-1). Is the function implementation simple and clear? Of course, because the scale of the problem is simple, it can actually be implemented using loops. You can try it.

Fibonacci Sequence

　Problem description: 1, 1, 2, 3, 5, 8, 13, 21, 34, ....... Find the nth number.

Code implementation:

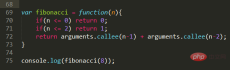
In fact, it is very simple to implement the idea just now. Through analysis, we can get the nth number, which is the sum of the first two numbers. Through this, we can continue to obtain the first two numbers we need through recursion until the condition n

　The problem of taking the stairs

　Problem description: There are n steps in the stairs. You can go up 1 step in one step or 2 steps in one step. Or level 3, count how many different moves there are.

Code implementation:

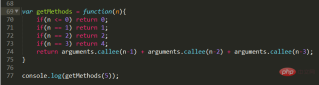
This is actually an implementation of the Fibonacci sequence. When we analyze, we can convert it into small-scale subclass problems. When reaching the last step of the designated ladder, there can be three situations: one is one step up, two is two steps up, and three is three steps up. So the overall method is F(n) = F(n-1) F(n-2) F(n-3). Then naturally it becomes their own small calculation, and the cycle continues until the judgment condition occurs.

　Greatest common divisor

Problem description: Given two numbers, if the two numbers are equal, the greatest common divisor is itself. If they are not equal, take the absolute value of the subtraction of the two numbers and compare it with the smallest of the two numbers. If they are equal, it is the greatest common denominator. If they are not equal, continue the above algorithm until they are equal.

Code implementation:

There is nothing to say, just implement it as required by the problem description. The exit of the recursion is that a equals b.

　

Tower of Hanoi

　Problem description: Everyone has played it more or less, so I won’t go into details here.

Code implementation:

Before I realized the essence of recursion, I was simply puzzled by this problem. I keep asking myself, how do I know where to go next? Later, I realized that I was actually more concerned about how to go about the last one. How do you say this? We can think from the beginning, if we only have one disk, we can make it go to column C or column B. Naturally, it can also be achieved with two disks. 3 disks is okay. Then let’s talk about the situation of 4 disks. To complete the four disks, the disk on A must be completely transferred to C. We put the first three disks as a whole on B, and then the fourth disk can be moved to C. Then we put the first three disks on C, and it was successful. The first three games can be treated as a new game, and the first two games can be treated as a whole, and so on. In this way, we only need to care about the big overall things, and other things can be solved into small-scale problems.

DichotomyQuick sort

Problem description: Use the dichotomy method to sort an array from small to large.

Code: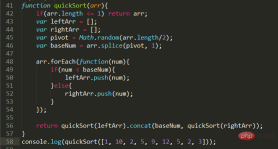

　

Well...this is my second time writing this. This time the implementation of recursion is much clearer than last time. In fact, it is also about reducing large scale to small scale, caring about a large whole, and letting it continue to be reduced to small scale for calculation. You can check the original essay for details.

Recursion of DOM tree

Problem description: Get the tagName of all parent nodes of a node

Code implementation:

　

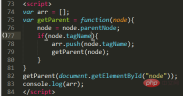
You can probably understand it and won’t say anything. Compared with the previous Tower of Hanoi and Quick Sort, this one is quite simple, but it is closest to the practical application of our JavaScript.

This article has ended here. For more other exciting content, you can pay attention to the JavaScript Video Tutorial column on the PHP Chinese website!

The above is the detailed content of Introduction to methods of implementing recursive algorithms in JavaScript. For more information, please follow other related articles on the PHP Chinese website!