Home >Java >javaTutorial >Basic method to implement binary search in Java (with code)
Basic method to implement binary search in Java (with code)
- 不言forward
- 2019-02-16 11:49:144596browse
The content of this article is about the basic method of implementing binary search in Java (with code). It has certain reference value. Friends in need can refer to it. I hope it will be helpful to you.
Binary search is particularly easy to understand. It is similar to the divide-and-conquer idea used in quick sort and merge. Each time, the middle number is compared with the target number, and then it is determined whether it is larger or smaller, and the interval is halved. .
For example:
Xiao Hong selected a number from 1-100 (this number is 56) and asked Xiao Ming to guess, resulting in the following dialogue:
Xiao Ming First guess: 68
Xiaohong: Too big
Xiao Ming’s second guess: 35
Xiaohong: Too small
Xiao Ming’s third guess First guess: 58
Xiaohong: Too big
Xiao Ming’s fourth guess: 49
Xiaohong: Too small
Xiao Ming’s fifth guess :54
小红:小红
Xiao Ming’s sixth guess: 56
小红: bingo! ! !
We can see that in the above conversation, Xiao Ming can narrow the range every time he guesses until the answer is correct
Binary search is like this. For example, we now have arrays 8, 11, 19 , 23, 27, 33, 45, 55, 67, 98, use binary search as shown below: 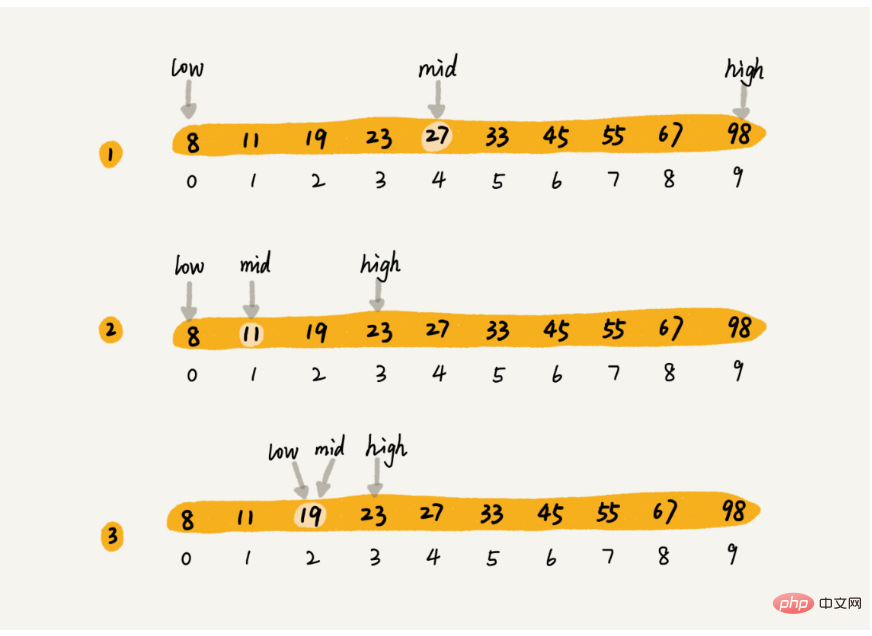
Each time you can reduce the interval by half, we can see that the interval changes as follows:

When the interval size is infinitely close to 1, k = log2n, so the time complexity is O(logn).
Is it particularly easy to understand? The following is a simple binary search I implemented in Java (note: it is the simplest implementation, the variants of binary search are very complicated and I have not yet mastered it)
package com.structure.search;
/**
* 二分查找法
*
* @author zhangxingrui
* @create 2019-02-15 21:29
**/
public class BinarySearch {
public static void main(String[] args) {
int[] nums = new int[]{4, 6, 9, 19, 30, 40, 500, 3450, 50004, 4334343};
System.out.println(binarySearch(nums, 0, nums.length - 1, 30));
System.out.println(binarySearch(nums, 50004));
}
/**
* @Author: xingrui
* @Description: 二分查找法(针对有序数组且不存在重复元素-递归方式实现)
* @Date: 21:37 2019/2/15
*/
private static int binarySearch(int[] nums, int p, int r, int k){
if(p > r)
return -1;
int mid = (p + r) / 2;
if(nums[mid] == k)
return mid;
if(k > nums[mid])
return binarySearch(nums, mid + 1, r, k);
else
return binarySearch(nums, p, mid - 1, k);
}
/**
* @Author: xingrui
* @Description: 二分查找法(针对有序数组且不存在重复元素-循环实现)
* @Date: 21:37 2019/2/15
*/
private static int binarySearch(int[] nums, int k){
int p = 0;
int r = nums.length - 1;
while (p <= r){
int mid = (p + r) / 2;
if(nums[mid] == k)
return mid;
if(k > nums[p])
p = mid + 1;
else
r = mid - 1;
}
return -1;
}
} The code is very simple, and what needs to be paid attention to is the boundary condition p<=r.
It can also be seen from the code that the simple implementation has great limitations and can only be applied to ordered arrays without duplicate data.
And binary search is not suitable for small-scale data query (because small-scale data query is not necessary), this is easy to understand; at the same time, it is not suitable for large-scale data query, why is this? Woolen cloth?
It is because of the above mentioned: binary search is suitable for the underlying data using arrays, but the array is a continuous memory space. When the data is large, if you want to use binary search, then the underlying implementation of the data Just
You can only use arrays, which is not very good. Assuming that my data has a G, then I have to apply for a continuous memory space of 1 G. Oh my god, I am afraid that I will be full.
The above is the detailed content of Basic method to implement binary search in Java (with code). For more information, please follow other related articles on the PHP Chinese website!

