Algorithm analysis of stack and queue in JavaScript

The content of this article is about the algorithm analysis of stacks and queues in JavaScript. It has certain reference value. Friends in need can refer to it. I hope it will be helpful to you.

1. Understanding data structure

What is data structure? The following is Wikipedia's explanation

Data structure is the way computers store and organize data

Data structure means interface or encapsulation: a data structure can be viewed as an interface between two functions, or as a data type The access method encapsulation of storage content composed of unions

We use data structures in our daily coding, because arrays are the simplest memory data structures. The following are common data structures

• Array

• Stack

• Queue

• Linked List

• Tree

• Graph

• Heap

• Hash table

Let’s learn about stacks and queues..

2. Stack

2.1 Stack data structure

The stack is an ordered collection that follows the last-in-first-out (LIFO) principle. Newly added or to be deleted elements are stored at the same end of the stack, called the top of the stack, and the other end is called the bottom of the stack. In the stack, new elements are near the top of the stack and old elements are near the bottom.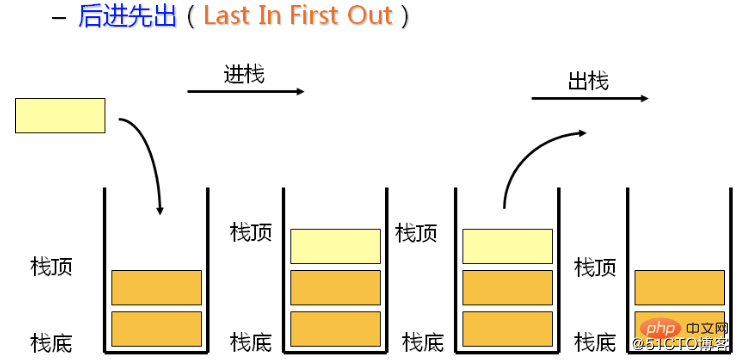

Analogy to objects in life: a stack of books or plates pushed together

2.2 Implementation of the stack

The following methods are commonly used in ordinary stacks:

push adds one (or several) new elements to the top of the stack

pop overflows the top element of the stack and returns the removed element

peek returns the top element of the stack without modifying the stack

isEmpty returns true if there are no elements in the stack, otherwise returns false

size returns the number of elements in the stack

clear Clear the stack

class Stack {
  constructor() {
    this._items = []; // 储存数据
  }
  // 向栈内压入一个元素
  push(item) {
    this._items.push(item);
  }
  // 把栈顶元素弹出
  pop() {
    return this._items.pop();
  }
  // 返回栈顶元素
  peek() {
    return this._items[this._items.length - 1];
  }
  // 判断栈是否为空
  isEmpty() {
    return !this._items.length;
  }
  // 栈元素个数
  size() {
    return this._items.length;
  }
  // 清空栈
  clear() {
    this._items = [];
  }
}

Now look back and think about what the stack is in the data structure.

Suddenly I discovered that it was not that magical, it was just an encapsulation of the original data. The result of encapsulation is: does not care about the elements inside it, but only operates the element on the top of the stack . In this case, the coding will be more controllable.

2.3 Application of stack

(1) Convert decimal to arbitrary number

Requirements: Given a function, input Target value and base, output the corresponding base number (maximum hexadecimal)

baseConverter(10, 2) ==> 1010
baseConverter(30, 16) ==> 1E

Analysis: The essence of base conversion: divide the target value by the base one at a time Base, the obtained rounded value is the new target value, record the remainder until the target value is less than 0, and finally combine the remainders in reverse order. Use the stack to record the remainder and push it into the stack, and pop it out when combining

// 进制转换
function baseConverter(delNumber, base) {
  const stack = new Stack();
  let rem = null;
  let ret = [];
  // 十六进制中需要依次对应A~F
  const digits = '0123456789ABCDEF';

  while (delNumber > 0) {
    rem = Math.floor(delNumber % base);
    stack.push(rem);
    delNumber = Math.floor(delNumber / base);
  }

  while (!stack.isEmpty()) {
    ret.push(digits[stack.pop()]);
  }

  return ret.join('');
}

console.log(baseConverter(100345, 2)); //输出11000011111111001
console.log(baseConverter(100345, 8)); //输出303771
console.log(baseConverter(100345, 16)); //输出187F9

(2) Reverse Polish expression calculation

Requirements: Reverse Polish expression Formula, also called a postfix expression, converts complex expressions into expressions that can rely on simple operations to obtain calculation results, such as (a b)*(c d) converted to a b c d *

["4", "13", "5", "/", "+"] ==> (4 + (13 / 5)) = 6
["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"]
==> ((10 * (6 / ((9 + 3) * -11))) + 17) + 5

Analysis: Use the symbol as the trigger node. Once the symbol is encountered, the first two elements of the symbol will be operated according to the symbol, and the new result will be pushed into the stack until the stack Only one element

function isOperator(str) {
  return ['+', '-', '*', '/'].includes(str);
}
// 逆波兰表达式计算
function clacExp(exp) {
  const stack = new Stack();
  for (let i = 0; i <p><strong> (3) Use a normal stack to implement a stack with a <code>min</code> method</strong></p><p><strong>Idea:</strong> Use There are two stacks to store data. One of them is named <code>dataStack</code>, which is specially used to store data, and the other is named <code>minStack</code>, which is specially used to store the smallest data in the stack. Always keep the number of elements in the two stacks the same. When pushing the stack, compare the size of the pushed element with the element at the top of <code>minStack</code>. If it is smaller than the element at the top of the stack, push it directly into the stack, otherwise copy the top of the stack. The element is pushed onto the stack; when the top of the stack is popped, just pop both. In this way, the top element of <code>minStack</code> is always the minimum value. </p><pre class="brush:php;toolbar:false">class MinStack {
  constructor() {
    this._dataStack = new Stack();
    this._minStack = new Stack();
  }

  push(item) {
    this._dataStack.push(item);
    // 为空或入栈元素小于栈顶元素，直接压入该元素
    if (this._minStack.isEmpty() || this._minStack.peek() > item) {
      this._minStack.push(item);
    } else {
      this._minStack.push(this._minStack.peek());
    }
  }

  pop() {
    this._dataStack.pop();
    return this._minStack.pop();
  }

  min() {
    return this._minStack.peek();
  }
}

const minstack = new MinStack();

minstack.push(3);
minstack.push(4);
minstack.push(8);
console.log(minstack.min()); // 3
minstack.push(2);
console.log(minstack.min()); // 2

3. Queue

3.1 Queue data structure

The queue follows the first-in-first-out (FIFO, also known as first-come-first-out An ordered set of items of service) principles. The queue adds new elements at the tail and removes elements from the top. The latest added element must be queued at the end of the queue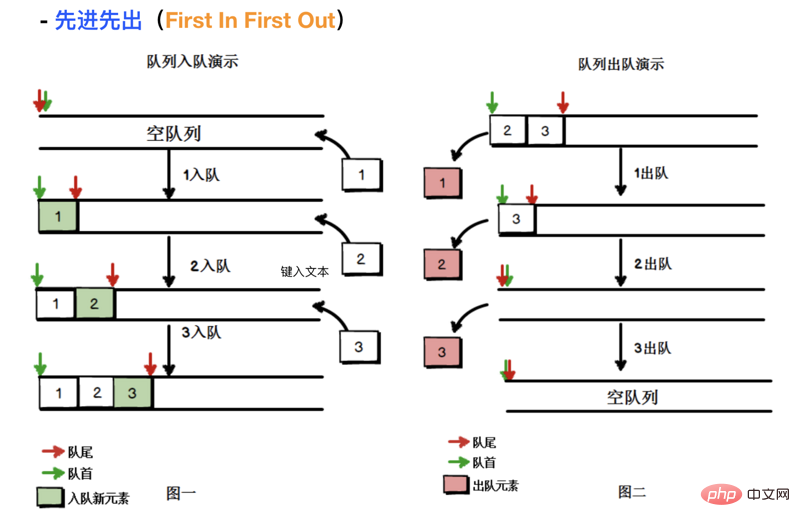

Analogy: Shopping queue in daily life

3.2 Queue implementation

Commonly used queues have the following methods:

• enqueue Add one (or more) new items to the end of the queue

• dequeue Remove the first item of the queue (that is, the front of the queue) and return the removed element

• head Return the first element of the queue without any changes to the queue

• tail Return the last element of the queue without any changes to the queue

• isEmpty 队列内无元素返回true，否则返回false

• size 返回队列内元素个数

• clear 清空队列

class Queue {
  constructor() {
    this._items = [];
  }

  enqueue(item) {
    this._items.push(item);
  }

  dequeue() {
    return this._items.shift();
  }

  head() {
    return this._items[0];
  }

  tail() {
    return this._items[this._items.length - 1];
  }

  isEmpty() {
    return !this._items.length;
  }

  size() {
    return this._items.length;
  }

  clear() {
    this._items = [];
  }
}

与栈类比，栈仅能操作其头部，队列则首尾均能操作，但仅能在头部出尾部进。当然，也印证了上面的话：栈和队列并不关心其内部元素细节，也无法直接操作非首尾元素。

3.3 队列的应用

（1）约瑟夫环（普通模式）

要求: 有一个数组a[100]存放0~99；要求每隔两个数删掉一个数，到末尾时循环至开头继续进行，求最后一个被删掉的数。

分析: 按数组创建队列，依次判断元素是否满足为指定位置的数，如果不是则enqueue到尾部，否则忽略，当仅有一个元素时便输出

// 创建一个长度为100的数组
const arr_100 = Array.from({ length: 100 }, (_, i) => i*i);

function delRing(list) {
  const queue = new Queue();
  list.forEach(e => { queue.enqueue(e); });
  
  let index = 0;
  while (queue.size() !== 1) {
    const item = queue.dequeue();
    index += 1;
    if (index % 3 !== 0) {
      queue.enqueue(item);
    }
  }

  return queue.tail();
}

console.log(delRing(arr_100)); // 8100 此时index=297

（2）菲波那切数列（普通模式）

要求: 使用队列计算斐波那契数列的第n项
分析: 斐波那契数列的前两项固定为1，后面的项为前两项之和，依次向后，这便是斐波那契数列。

function fibonacci(n) {
    const queue = new Queue();
    queue.enqueue(1);
    queue.enqueue(1);
    
    let index = 0;
    while(index <p><strong>（3）用队列实现一个栈</strong></p><p><strong>要求:</strong> 用两个队列实现一个栈<br><strong>分析:</strong> 使用队列实现栈最主要的是在队列中找到栈顶元素并对其操作。具体的思路如下：</p><ol class=" list-paddingleft-2">
<li><p>两个队列，一个备份队列<code>emptyQueue</code>，一个是数据队列<code>dataQueue</code>；</p></li>
<li><p>在确认栈顶时，依次<code>dequeue</code>至备份队列，置换备份队列和数据队列的引用即可</p></li>
</ol><pre class="brush:php;toolbar:false">class QueueStack {
  constructor() {
    this.queue_1 = new Queue();
    this.queue_2 = new Queue();
    this._dataQueue = null; // 放数据的队列
    this._emptyQueue = null; // 空队列,备份使用
  }

  // 确认哪个队列放数据,哪个队列做备份空队列
  _initQueue() {
    if (this.queue_1.isEmpty() && this.queue_2.isEmpty()) {
      this._dataQueue = this.queue_1;
      this._emptyQueue = this.queue_2;
    } else if (this.queue_1.isEmpty()) {
      this._dataQueue = this.queue_2;
      this._emptyQueue = this.queue_1;
    } else {
      this._dataQueue = this.queue_1;
      this._emptyQueue = this.queue_2;
    }
  };

  push(item) {
    this.init_queue();
    this._dataQueue.enqueue(item);
  };

  peek() {
    this.init_queue();
    return this._dataQueue.tail();
  }

  pop() {
    this.init_queue();
    while (this._dataQueue.size() > 1) {
      this._emptyQueue.enqueue(this._dataQueue.dequeue());
    }
    return this._dataQueue.dequeue();
  };
};

学习了栈和队列这类简单的数据结构，我们会发现。数据结构并没有之前想象中那么神秘，它们只是规定了这类数据结构的操作方式：栈只能对栈顶进行操作，队列只能在尾部添加在头部弹出；且它们不关心内部的元素状态。

The above is the detailed content of Algorithm analysis of stack and queue in JavaScript. For more information, please follow other related articles on the PHP Chinese website!