Introduction to binary trees (binary heaps) in JavaScript (code examples)

This article brings you an introduction (code example) about binary trees (binary heaps) in JavaScript. It has certain reference value. Friends in need can refer to it. I hope it will be helpful to you.

Binary Tree

Binary Tree (Binary Tree) is a tree structure. Its characteristic is that each node has at most two branch nodes. A binary tree usually consists of It consists of root node, branch node and leaf node. Each branch node is often called a subtree.

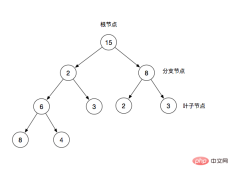
• Root node: the top node of the binary tree

• Branch node: In addition to the root node and has leaf nodes

• Leaf node: except itself, has no other child nodes

Common terms

In a binary tree, we often use parent nodes and child nodes to describe it. For example, 2 in the figure is the parent node of 6 and 3, and conversely 6 and 3 are the child nodes of 2

Three properties of binary trees

1. ##On the i-th level of the binary tree, there are at most 2^i-1 nodes

• When i=1, there is only one root node, 2^(i-1) = 2^0 = 1

The binary tree with depth k is at most There are 2^k-1 nodes

• When i=2, 2^k-1 = 2^2 - 1 = 3 nodes

For any binary tree T, if the number of summary points is n0 and the number of nodes with degree 2 (number of subtrees is 2) is n2, then n0=n2 1

Three main differences between trees and binary trees

• The number of nodes of a tree is at least 1, while the number of nodes of a binary tree can be 0

• There is no limit to the maximum degree (number of nodes) of a node in a tree, while the maximum degree of a node in a binary tree is 2

• There is no left or right distinction between the nodes of a tree, while the nodes of a binary tree There are left and right sides

Binary tree classification

Binary trees are divided into complete binary trees and full binary trees

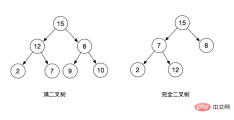
• Full binary tree: A binary tree with depth k and 2^k - 1 nodes is called a full binary tree

• Complete binary tree: A complete binary tree refers to the left side of the last layer It is full, the right side may be full or not full, and the remaining levels are full. The binary tree is called a complete binary tree (a full binary tree is also a complete binary tree)

Array representation of binary tree

Use an array to represent the structure of the binary tree. Fill a set of arrays into an array starting from the root node from top to bottom and from left to right. In a complete binary tree, as shown in the following figure

Through the above figure we can analyze that the complete binary tree represented by the array has the following properties:

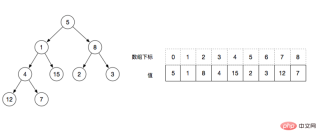
• left = index * 2 1, for example: the subscript of the root node is 0, then the value of the left node is the subscript array[0＊2 1]=1

• right = index * 2 2, for example: the subscript of the root node is 0, then the value of the right node is the subscript array[0*2 2]=2

• Ordinal>= floor(N/2) are all leaf nodes, for example: floor(9/2) = 4, then the values ​​starting from subscript 4 are all leaf nodes

Binary Heap

The structure of a binary heap is represented by a complete binary tree, which is represented by an array, but a binary heap needs to meet the following properties:

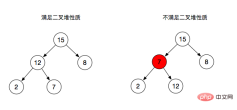
• The key value of the parent node of the binary heap is always greater than or equal to (less than or equal to) the key value of any child node

• When the key value of the parent node is greater than or equal to ( Less than or equal to) the key value of each of its child nodes, it is called

  max heap (minimum heap)

  

As can be seen from the above picture:

• Left picture: The parent node is always greater than or equal to its child node , so it satisfies the properties of a binary heap,

• Right picture: Branch node 7, as the parent node of 2 and 12, does not satisfy its properties (greater than or equal to the child node).

Main operations of binary heap

• insert: insert node

• delete: delete node

• max-hepify: Adjust branch node heap properties

• rebuildHeap: Rebuild the entire binary heap

• sort: Sort

Initialize a binary heap

From the above brief introduction, we can know that the initialization of a binary heap is very simple. It’s just an array

• Initialize an array structure

• Save the array length

    class Heap{
        constructor(arr){
            this.data = [...arr];
            this.size = this.data.length;
        }
    }

max-heapify maximum heap operation

max-heapify is to convert each item that does not satisfy the maximum heap properties An operation for adjusting branch nodes.

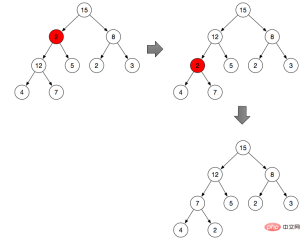
As shown above:

1. Adjust branch node 2 (branch node 2 does not meet the properties of the maximum heap )

• By default, the branch node is the maximum value

Compare 2 with the left and right branches, from 2, 12, Find the maximum value in 5, and then exchange the position with 2

• According to the binary heap properties above, get the left node and right node of branch node 2 respectively

• Compare three nodes and get the subscript max of the maximum value

• If the node itself is the maximum value, stop the operation

• Exchange the max node with the parent node

Repeat the operation of step 2, find the maximum value from 2, 4, and 7 and exchange it with 2

• Recursion

    maxHeapify(i) {
        let max = i;
        
        if(i >= this.size){
            return;
        }
        // 当前序号的左节点
        const l = i * 2 + 1;
        // 当前需要的右节点
        const r = i * 2 + 2;
        
        // 求当前节点与其左右节点三者中的最大值
        if(l  this.data[max]){
            max = l;
        }
        if(r  this.data[max]){
            max = r;
        }
        
        // 最终max节点是其本身,则已经满足最大堆性质，停止操作
        if(max === i) {
            return;
        }
        
        // 父节点与最大值节点做交换
        const t = this.data[i];
        this.data[i] = this.data[max];
        this.data[max] = t;
        
        // 递归向下继续执行
        return this.maxHeapify(max);
    }

Reconstructing the heap

We can see that the newly initialized heap Represented by an array, at this time it may not satisfy the properties of a maximum heap or a minimum heap. At this time, we may need to build the entire heap into what we want.
We did the max-heapify operation above, and max-heapify only adjusts a certain branch node. To build the entire heap into a maximum heap, you need to perform a max-heapify operation on all branch nodes. As shown in the figure below, we need to perform max-hepify operations on the four branch nodes 12, 3, 2, and 15 in sequence

##Specific steps:

• Find all branch nodes: The properties of the heap mentioned above mentioned that the serial number of the leaf node>=Math.floor(n/2), so it is smaller than the serial number of Math.floor(n/2) These are all nodes we need to adjust.

• For example, the array shown in the middle is [15,2,3,12,5,2,8,4,7] => Math.floor(9/2 )=4 => Those with index less than 4 are 15, 2, 3, and 12 (nodes that need to be adjusted), while 5, 2, 8, 4, and 7 are leaf nodes.

• Perform maxHeapify operation on all found nodes

    rebuildHeap(){
        // 叶子节点
        const L = Math.floor(this.size / 2);
        for(let i = L - 1; i>=0; i--){
            this,maxHeapify(i);
        }
    }

Maximum heap sort

The sorting of the largest heap, as shown in the figure above:

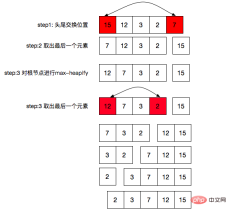
• Exchange the first and last positions

• Change the last The element is taken out from the heap, which is equivalent to the size-1 of the heap

• Then perform a max-heapify operation on the root node of the heap

• Repeat In the above three steps, we know that size=0 (we have already done this boundary condition in the max-heapify function)

    sort() {
        for(let i = this.size - 1; i > 0; i--){
            swap(this.data, 0, i);
            this.size--;
            this.maxHeapify(0);
        }
    }

Insertion and deletion

The insertion and deletion of this Deletion is relatively simple, it is the operation of inserting and deleting an array

• Insert to the end

• Heap length 1

• Determine whether it is still a maximum heap after insertion

• If not, reconstruct the heap

  insert(key) {
    this.data[this.size] = key;
    this.size++
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

• Delete an element in the array

• Heap length-1

• Determine whether it is a heap

• If not, then reconstruct the heap

  delete(index) {
    if (index >= this.size) {
      return;
    }
    this.data.splice(index, 1);
    this.size--;
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

Complete code

/**
 * 最大堆
 */

function left(i) {
  return i * 2 + 1;
}

function right(i) {
  return i * 2 + 2;
}

function swap(A, i, j) {
  const t = A[i];
  A[i] = A[j];
  A[j] = t;
}

class Heap {
  constructor(arr) {
    this.data = [...arr];
    this.size = this.data.length;
  }

  /**
   * 重构堆
   */
  rebuildHeap() {
    const L = Math.floor(this.size / 2);
    for (let i = L - 1; i >= 0; i--) {
      this.maxHeapify(i);
    }
  }

  isHeap() {
    const L = Math.floor(this.size / 2);
    for (let i = L - 1; i >= 0; i++) {
      const l = this.data[left(i)] || Number.MIN_SAFE_INTEGER;
      const r = this.data[right(i)] || Number.MIN_SAFE_INTEGER;

      const max = Math.max(this.data[i], l, r);

      if (max !== this.data[i]) {
        return false;
      }
      return true;
    }
  }

  sort() {
    for (let i = this.size - 1; i > 0; i--) {
      swap(this.data, 0, i);
      this.size--;
      this.maxHeapify(0);
    }
  }

  insert(key) {
    this.data[this.size++] = key;
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

  delete(index) {
    if (index >= this.size) {
      return;
    }
    this.data.splice(index, 1);
    this.size--;
    if (this.isHeap()) {
      return;
    }
    this.rebuildHeap();
  }

  /**
   * 堆的其他地方都满足性质
   * 唯独跟节点，重构堆性质
   * @param {*} i
   */
  maxHeapify(i) {
    let max = i;

    if (i >= this.size) {
      return;
    }

    // 求左右节点中较大的序号
    const l = left(i);
    const r = right(i);
    if (l  this.data[max]) {
      max = l;
    }

    if (r  this.data[max]) {
      max = r;
    }

    // 如果当前节点最大，已经是最大堆
    if (max === i) {
      return;
    }

    swap(this.data, i, max);

    // 递归向下继续执行
    return this.maxHeapify(max);
  }
}

module.exports = Heap;

Summary

The heap is over here, the heap is Binary trees are relatively simple and are often used for sorting and priority queues. The core of the heap is the max-heapify operation and the three properties of the heap.

The above is the detailed content of Introduction to binary trees (binary heaps) in JavaScript (code examples). For more information, please follow other related articles on the PHP Chinese website!