Home >Web Front-end >JS Tutorial >Detailed case explanation: Introduction to dynamic programming (taking stairs as an example)
Detailed case explanation: Introduction to dynamic programming (taking stairs as an example)
- php是最好的语言Original
- 2018-08-09 16:33:274046browse
Concept
Dynamic programming (dynamic programming) is a branch of operations research and a mathematical method for optimizing the decision process.
Dynamic programming algorithms are usually based on a recursion formula and one or more initial states. The solution to the current subproblem will be derived from the solution to the previous subproblem .
Basic idea
To solve a given problem, we need to solve its different parts (i.e.solve subproblems), and then combine the solutions of the subproblems to get Solution to the original problem.
Usually many sub-problems are very similar, so the dynamic programming method tries to only solve each sub-problem once , thereby reducing the amount of calculation.
Once the solution to a given sub-problem has been calculated, it is memorized and stored so that the next time the solution to the same sub-problem is needed, the table can be directly looked up.
This approach is particularly useful when the number of repeated subproblems grows exponentially with the size of the input.
Dynamic programming has three core elements:
1. Optimal substructure
2. Boundary
3. State transition equation
Let’s take a look at the question
题
There is a staircase with a height of 10 steps. Walking from bottom to top, each step can only go up 1 or 2 steps. Find how many moves there are in total.
For example, taking one step at a time, taking a total of 10 steps, is one of the walking methods.
For another example, take 2 steps each time, taking a total of 5 steps. This is another way of walking.
But it’s too troublesome to calculate each step like this. We can just think about how to take the last step, as shown below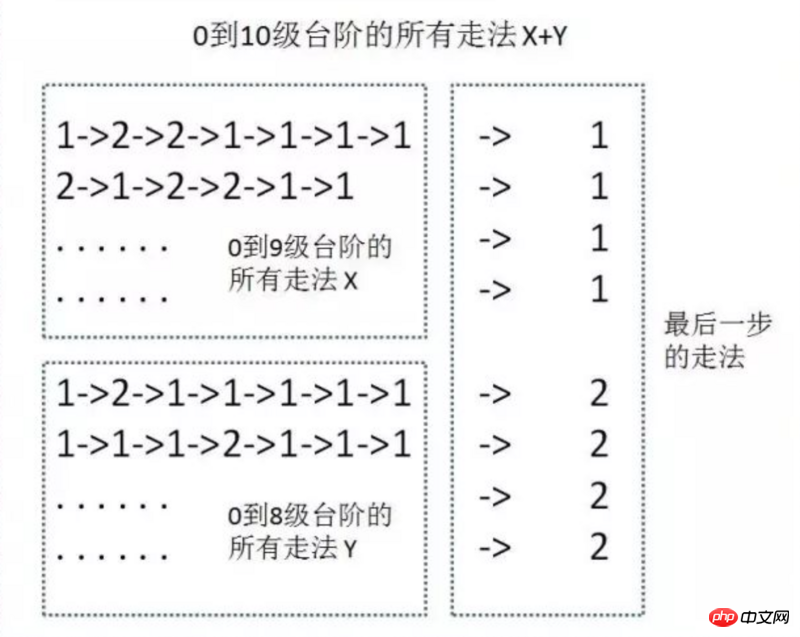
How to get to the tenth staircase= Go to the eighth stair and go to the ninth stair
We use f(n) to represent the way to go to the nth stair, so we have f(10) = f(9) f(8)
Then f(9) = f(8) f(7), f(8) = f(7) f(6)......
In this way we will get aRecursive formula:
f(n) = f(n-1) f(n-2);
There are also two Initial states :
f(1) = 1;
f(2) = 2;
This gives us the first solution
Method 1: Recursive solution
function getWays(n) {
if (n < 1) return 0;
if (n == 1) return 1;
if (n == 2) return 2;
return getWays(n-1) + getWays(n-2);
}The time complexity of this method isO(2^n)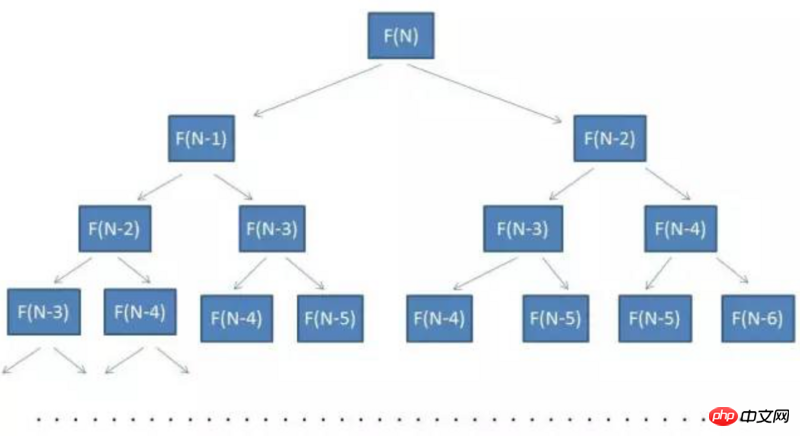
You can see that this is a binary tree. The number of nodes is the number of times our recursive equation needs to be calculated.
The height of the number is N, and the number of nodes is approximately 2^n
so the time is complicated The degree is approximately O(2^n)
, but can this method be optimized?
We will find that some values are repeatedly calculated, as shown in the figure below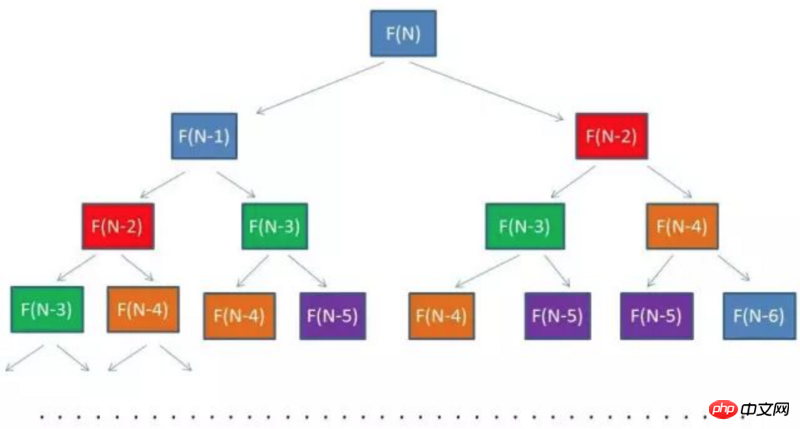 The same color represents the repeated parts, so can we record these repeatedly calculated values?
The same color represents the repeated parts, so can we record these repeatedly calculated values?
There is a second method for such optimization
Method 2: Memo Algorithm
const map = new Map();
function getWays(n) {
if (n < 1) return 0;
if (n == 1) return 1;
if (n == 2) return 2;
if (map.has(n)) {
return map.get(n);
}
const value = getWays(n-1) + getWays(n-2);
map.set(n, value);
return value;
}Because n-2 key-value pairs will eventually be stored in the map , so the space complexity is O(n), and the time complexity is also O(n)
. Keep thinking about it. This is the optimal solution. ?
Let’s go back to the original idea. We assume that the previous stairs have been walked and only consider the last step, so we come to f(n) = f(n-1) f(n-2) The recursive formula of See if it works
This is the number of moves for one and two stairs at the beginning, which is the  initial state
initial state
 Continue to the next step
Continue to the next step
Here another iteration is performed to obtain the steps of 4 stairs. f(4) only depends on f(2) and f(3) We find that each iteration only requires the results of the first two iterations. Data, there is no need to save the data of all sub-states like a memo
We find that each iteration only requires the results of the first two iterations. Data, there is no need to save the data of all sub-states like a memo
Method 3: Dynamic programming solution
function getWays(n) {
if (n < 1) return 0;
if (n == 1) return 1;
if (n == 2) return 2;
// a保存倒数第二个子状态数据,b保存倒数第一个子状态数据, temp 保存当前状态的数据
let a = 1, b = 2;
let temp = a + b;
for (let i = 3; i <= n; i++) {
temp = a + b;
a = b;
b = temp;
}
return temp;
}
This is where we can look at the current time complexity And space complexityThe current time complexity is still
O(n)
, but the space complexity is reduced toO(1)This is the ideal result
Summary
This is just one of the simplest questions in dynamic programming, because it has only one change dimension
When the change dimensions become two, three or even more, it will be more complicated , the knapsack problem is a typical multi-dimensional problem. If you are interested, you can go online and read "Nine Lectures on Backpacks"Related recommendations:
Detailed explanation of the use of JS dynamic programming
JavaScript advanced algorithm dynamic programming example analysis
The above is the detailed content of Detailed case explanation: Introduction to dynamic programming (taking stairs as an example). For more information, please follow other related articles on the PHP Chinese website!
Related articles
See more- An in-depth analysis of the Bootstrap list group component
- Detailed explanation of JavaScript function currying
- Complete example of JS password generation and strength detection (with demo source code download)
- Angularjs integrates WeChat UI (weui)
- How to quickly switch between Traditional Chinese and Simplified Chinese with JavaScript and the trick for websites to support switching between Simplified and Traditional Chinese_javascript skills

