js_Three algorithms for binary tree traversal in front, middle and back order_implementation of simple binary tree

Regarding the establishment and traversal of binary trees, this article gives a detailed introduction, and the algorithms of pre-order binary tree traversal, in-order binary tree traversal, and post-order binary tree traversal are also explained, and the code is quoted for the purpose of making it easier to Everyone can see it more clearly. The introduction of this article should start with binary trees and binary search trees for easy understanding. apache php mysql

Binary tree and binary search tree

Related terms about the tree:

Node: Each element in the tree Called a node,

Root node: A node located at the vertex of the entire tree. It has no parent node, as shown in Figure 5

Child nodes: Descendants of other nodes

Leaves Node: Elements without child nodes are called leaf nodes, as shown in Figure 3 8 24

Binary tree: A binary tree is a data structure, and its organizational relationship is like a tree in nature. The official language definition is: It is a set of finite elements, which is either empty or consists of an element called the root and two disjoint binary trees called the left subtree and the right subtree respectively.

Binary search tree:
Binary search tree is also called binary search tree (BST). It only allows us to store a smaller value in the left node than the parent node, and a smaller value in the right node than the parent node. For larger values, the picture above shows a binary search tree.

Code implementation

First create a class to represent a binary search tree. There should be a Node class inside it to create nodes

    function BinarySearchTree () {
        var Node = function(key) {
            this.key = key,
            this.left = null,
            this.right = null
        }
        var root = null
    }

It should also have some Method:

• insert(key) Insert a new key

• inOrderTraverse() Perform in-order traversal of the tree and print the result

• preOrderTraverse() Performs a pre-order traversal of the tree and prints the results

• postOrderTraverse() Performs a post-order traverse of the tree and prints the results

• search(key) searches for the key in the tree, returns true if it exists, returns fasle if it does not exist

• findMin() returns the minimum value in the tree

• findMax() Returns the maximum value in the tree

• remove(key) Delete a key in the tree

Insert a key into the tree

Insert a new key into the tree. The homepage should create a Node class instance to represent the new node, so you need to new the Node class and pass it in The key value that needs to be inserted will be automatically initialized to a new node with null left and right nodes

Then, some judgments need to be made. First, judge whether the tree is empty. If it is empty, the newly inserted node will be used as the root. Node, if it is not empty, call an auxiliary method insertNode() method, pass the root node and new node into

    this.insert = function(key) {
        var newNode = new Node(key)
        if(root === null) {
            root = newNode
        } else {
            insertNode(root, newNode)
        }
    }

Define the insertNode() method, this method will call itself recursively to find the new node. Add the appropriate position of the node

    var insertNode = function(node, newNode) {
        if (newNode.key <= node.key) {
            if (node.left === null) {
                node.left = newNode
            }else {
                insertNode(node.left, newNode)
            }
        }else {
            if (node.right === null) {
                node.right = newNode
            }else {
                insertNode(node.right, newNode)
            }
        }
    }

Complete the in-order traversal method

To implement the in-order traversal, we need an inOrderTraverseNode(node) method, which can call itself recursively to traverse each node

    this.inOrderTraverse = function() {
        inOrderTraverseNode(root)
    }

This method will print the key value of each node. It requires a recursive termination condition - check whether the incoming node is null. If it is not null, continue to call itself recursively to check the left and left of the node. Right node
is also very simple to implement:

    var inOrderTraverseNode = function(node) {
        if (node !== null) {
            inOrderTraverseNode(node.left)
            console.log(node.key)
            inOrderTraverseNode(node.right)
        }
    }

Pre-order traversal, post-order traversal

With the method of mid-order traversal, you only need to make slight changes to achieve pre-order. Traversal and post-order traversal
The above code:

In this way, the entire tree can be traversed in in-order

    // 实现先序遍历
    this.preOrderTraverse = function() {
        preOrderTraverseNode(root)
    }
    var preOrderTraverseNode = function(node) {
        if (node !== null) {
            console.log(node.key)
            preOrderTraverseNode(node.left)
            preOrderTraverseNode(node.right)
        }
    }

    // 实现后序遍历
    this.postOrderTraverse = function() {
        postOrderTraverseNode(root)
    }
    var postOrderTraverseNode = function(node) {
        if (node !== null) {
            postOrderTraverseNode(node.left)
            postOrderTraverseNode(node.right)
            console.log(node.key)
        }
    }

Did you find it? In fact, the internal statements change the front and rear positions. This also happens to conform to the three traversal rules: pre-order traversal (root-left-right), mid-order traversal (left-root-right), mid-order traversal (left-right-root)

Do it first Let’s test it

The complete code now is as follows:

    function BinarySearchTree () {
        var Node = function(key) {
            this.key = key,
            this.left = null,
            this.right = null
        }
        var root = null
        
        //插入节点
        this.insert = function(key) {
            var newNode = new Node(key)
            if(root === null) {
                root = newNode
            } else {
                insertNode(root, newNode)
            }
        }
        var insertNode = function(node, newNode) {
            if (newNode.key <= node.key) {
                if (node.left === null) {
                    node.left = newNode
                }else {
                    insertNode(node.left, newNode)
                }
            }else {
                if (node.right === null) {
                    node.right = newNode
                }else {
                    insertNode(node.right, newNode)
                }
            }
        } 
        
        //实现中序遍历
        this.inOrderTraverse = function() {
            inOrderTraverseNode(root)
        }
        var inOrderTraverseNode = function(node) {
            if (node !== null) {
                inOrderTraverseNode(node.left)
                console.log(node.key)
                inOrderTraverseNode(node.right)
            }
        }
        // 实现先序遍历
        this.preOrderTraverse = function() {
            preOrderTraverseNode(root)
        }
        var preOrderTraverseNode = function(node) {
            if (node !== null) {
                console.log(node.key)
                preOrderTraverseNode(node.left)
                preOrderTraverseNode(node.right)
            }
        }

        // 实现后序遍历
        this.postOrderTraverse = function() {
            postOrderTraverseNode(root)
        }
        var postOrderTraverseNode = function(node) {
            if (node !== null) {
                postOrderTraverseNode(node.left)
                postOrderTraverseNode(node.right)
                console.log(node.key)
            }
        }
    }

has actually completed the method of adding new nodes and traversing, let’s test it:

Define an array, There are some elements in it

var arr = [9,6,3,8,12,15]

We insert each element in arr into the binary search tree accordingly, and then print the result

    var tree = new BinarySearchTree()
    arr.map(item => {
        tree.insert(item)
    })
    tree.inOrderTraverse()
    tree.preOrderTraverse()
    tree.postOrderTraverse()

After running the code, let’s first take a look at the inserted node The final situation of the entire tree:

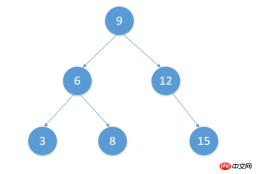
Output result

In-order traversal: <br>3<br>6<br>8<br>9<br>12<br>15<br>

Preorder traversal: <br>9<br>6<br>3<br>8<br>12 <br>15<br>

Post-order traversal: <br>3<br>8<br>6<br>15<br>12<br>9<br>

Obviously, the results are as expected, so we use the above JavaScript code to implement node insertion into the tree and three traversal methods. At the same time, it is obvious that in Binary search tree species, the value of the leftmost node is the smallest, and the value of the rightmost node is the largest, so the binary search tree can easily get the maximum and minimum values

Find the minimum and maximum values

How to do it? In fact, you only need to pass the root node into the minNode/or maxNode method, and then judge the node as the left (minNode)/right (maxNode) node through a loop as null

Implementation code:

    // 查找最小值
    this.findMin = function() {
        return minNode(root)
    }
    var minNode = function(node) {
        if (node) {
            while (node && node.left !== null) {
                node = node.left
            }
            return node.key
        }
        return null
    }
    
    // 查找最大值
    this.findMax = function() {
        return maxNode(root)
    }
    var maxNode = function (node) {
        if(node) {
            while (node && node.right !== null) {
                node =node.right
            }
            return node.key
        }
        return null
    }

所搜特定值

this.search = function(key) {
    return searchNode(root, key)
}

同样，实现它需要定义一个辅助方法,这个方法首先会检验node的合法性，如果为null，直接退出，并返回fasle。如果传入的key比当前传入node的key值小，它会继续递归查找node的左侧节点，反之，查找右侧节点。如果找到相等节点，直接退出，并返回true

    var searchNode = function(node, key) {
        if (node === null) {
            return false
        }
        if (key < node.key) {
            return searchNode(node.left, key)
        }else if (key > node.key) {
            return searchNode(node.right, key)
        }else {
            return true
        }
    }

移除节点

移除节点的实现情况比较复杂，它会有三种不同的情况：

• 
  

• 需要移除的节点是一个叶子节点

• 需要移除的节点包含一个子节点

• 需要移除的节点包含两个子节点

和实现搜索指定节点一元，要移除某个节点，必须先找到它所在的位置，因此移除方法的实现中部分代码和上面相同：

    // 移除节点
    this.remove = function(key) {
        removeNode(root,key)
    }
    var removeNode = function(node, key) {
        if (node === null) {
            return null
        }
        if (key < node.key) {
            node.left = removeNode(node.left, key)
            return node
        }else if(key > node.key) {
            node.right = removeNode(node.right,key)
            return node
        }else{
            //需要移除的节点是一个叶子节点
            if (node.left === null && node.right === null) {
                node = null
                return node
            }
            //需要移除的节点包含一个子节点
            if (node.letf === null) {
                node = node.right
                return node
            }else if (node.right === null) {
                node = node.left
                return node
            }
            //需要移除的节点包含两个子节点
            var aux = findMinNode(node.right)
            node.key = aux.key
            node.right = removeNode(node.right, axu.key)
            return node
        }
    }
    var findMinNode = function(node) {
        if (node) {
            while (node && node.left !== null) {
                node = node.left
            }
            return node
        }
        return null
    }

其中，移除包含两个子节点的节点是最复杂的情况，它包含左侧节点和右侧节点，对它进行移除主要需要三个步骤：

1. 需要找到它右侧子树中的最小节点来代替它的位置

2. 将它右侧子树中的最小节点移除

3. 将更新后的节点的引用指向原节点的父节点

有点绕儿，但必须这样，因为删除元素后的二叉搜索树必须保持它的排序性质

测试删除节点

tree.remove(8)
tree.inOrderTraverse()

打印结果：

3<br>6<br>9<br>12<br>15<br>

8 这个节点被成功删除了，但是对二叉查找树进行中序遍历依然是保持排序性质的

到这里，一个简单的二叉查找树就基本上完成了，我们为它实现了，添加、查找、删除以及先中后三种遍历方法

存在的问题

但是实际上这样的二叉查找树是存在一些问题的，当我们不断的添加更大/更小的元素的时候，会出现如下情况：

tree.insert(16)
tree.insert(17)
tree.insert(18)

来看看现在整颗树的情况：

看图片容易得出它是不平衡的，这又会引出平衡树的概念，要解决这个问题，还需要更复杂的实现，例如：AVL树，红黑树 哎，之后再慢慢去学习吧

相关文章：

二叉树遍历算法-php的示例

二叉树的中序遍历,该怎么解决

The above is the detailed content of js_Three algorithms for binary tree traversal in front, middle and back order_implementation of simple binary tree. For more information, please follow other related articles on the PHP Chinese website!