Basic and commonly used algorithms in Python

This article mainly focuses on learning common algorithms in Python and common sorting algorithms in Python, which has a certain reference value. Interested friends can refer to it

The content of this section

Algorithm definition
Time complexity
Space complexity
Commonly used algorithm examples

##1.Algorithm definition

Algorithm refers to an accurate and complete description of a problem-solving solution. It is a series of clear instructions for solving problems. Algorithm represents a systematic method to describe the strategic mechanism for solving problems. In other words, it is possible to obtain the required output within a limited time for a certain specification of input. If an algorithm is flawed or inappropriate for a problem, executing the algorithm will not solve the problem. Different algorithms may use different time, space, or efficiency to complete the same task. The quality of an algorithm can be measured by its space complexity and time complexity.

An algorithm should have the following seven important characteristics:

①Finiteness: The finiteness of an algorithm means that the algorithm must be able to terminate after executing a limited number of steps;

②Definiteness: Each step of the algorithm must have an exact definition;

③Input: An algorithm has 0 or more inputs to describe the operand The so-called 0 inputs refer to the initial conditions set by the algorithm itself;

④Output: An algorithm has one or more outputs to reflect the results of processing the input data . An algorithm without output is meaningless;

⑤Effectiveness: Any calculation steps performed in the algorithm can be decomposed into basic executable operation steps, that is, each calculation step All can be completed within a limited time (also called effectiveness);

⑥High efficiency: fast execution and less resource usage;

⑦Robustness : Correct response to data.

2. Time complexity

In computer science, the time complexity of an algorithm is a function that quantitatively describes the operation of the algorithm. Time, time complexity commonly used Big O notation (Big O notation) is a mathematical notation used to describe the asymptotic behavior of a function. More precisely, it is a function that is described in terms of another (usually simpler) function The asymptotic upper bound of the order of magnitude. In mathematics, it is generally used to describe the remaining terms of truncated infinite series, especially asymptotic series; in computer science, it is very useful in analyzing the complexity of algorithms. , using this method, the time complexity can be said to be asymptotic, which considers the situation when the size of the input value approaches infinity.

Big O, in short, it can be considered to mean "order of" (approximately).

Infinite asymptotic

Big O notation is very useful when analyzing the efficiency of an algorithm. For example, the time it takes to solve a problem of size n (or the number of steps required) can be found: T(n) = 4n^2 - 2n + 2.

When n increases, the n^2; term will start to dominate, and the other terms can be ignored - for example: when n = 500, the 4n^2; term is 1000 times larger than the 2n term, Therefore, in most cases, the effect of omitting the latter on the value of the expression will be negligible.

Mathematical Representation Literacy Post Python Algorithm Representation Concept Literacy Tutorial

1. Calculation method

1. The time it takes to execute an algorithm , it cannot be calculated theoretically, and it can only be known by running a test on the computer. But it is impossible and unnecessary for us to test every algorithm on the computer. We only need to know which algorithm takes more time and which algorithm takes less time. And the time an algorithm takes is proportional to the number of executions of statements in the algorithm. Whichever algorithm has more statements is executed, it takes more time.

The number of statement executions in an algorithm is called statement frequency or time frequency. Denote it as T(n).

2. Generally, the number of times the basic operation of the algorithm is repeated is a function f(n) of module n. Therefore, the time complexity of the algorithm is recorded as: T ( n)=O(f(n)). As module n increases, the growth rate of the algorithm execution time is proportional to the growth rate of f(n). Therefore, the smaller f(n) is, the lower the time complexity of the algorithm is and the higher the efficiency of the algorithm is.

When calculating the time complexity, first find out the basic operations of the algorithm, then determine the number of executions based on the corresponding statements, and then find the same order of magnitude of T(n) (its same order of magnitude are as follows: 1 , Log2n, n, nLog2n, n square, n cube, 2 n power, n!), after finding out, f (n) = this order of magnitude, if T (n)/f (n) find the limit A constant c can be obtained, and the time complexity T(n)=O(f(n)).

3. Common time complexities

Arranged in increasing order of magnitude, common time complexities include:

Constant order O(1), Logarithmic order O(log2n), linear order O(n), linear logarithmic order O(nlog2n), square order O(n^2), cubic order O(n^3),..., kth power order O(n ^k), exponential order O(2^n).
in,

1.O(n), O(n^2), cubic order O(n^3),..., kth order O(n^k) are polynomial order time complexity, respectively called First-order time complexity, second-order time complexity. . . .
2.O(2^n), exponential time complexity, this kind of impractical
3. Logarithmic order O(log2n), linear logarithmic order O(nlog2n), except for constant order, this The most efficient one

Example: Algorithm:

 for（i=1;i<=n;++i）
 {
 for(j=1;j<=n;++j)
 {
 c[ i ][ j ]=0; //该步骤属于基本操作 执行次数：n^2
 for(k=1;k<=n;++k)
 c[ i ][ j ]+=a[ i ][ k ]*b[ k ][ j ]; //该步骤属于基本操作 执行次数：n^3
 }
 }

Then there is T(n)=n^2+n^3, According to the same order of magnitude in the brackets above, we can determine that n^3 is the same order of magnitude as T(n)
Then f(n) = n^3, and then find the limit according to T(n)/f(n) Obtain the constant c
, then the time complexity of the algorithm: T(n)=O(n^3)

4. Definition: If the scale of a problem is n , the time required for a certain algorithm to solve this problem is T(n), which is a certain function of n. T(n) is called the "time complexity" of this algorithm.

When the input quantity n gradually increases, the limit situation of time complexity is called the "asymptotic time complexity" of the algorithm.

We often use big O notation to express time complexity. Note that it is the time complexity of a certain algorithm. Big O means that there is an upper bound. By definition, if f(n)=O(n), then f(n)=O(n^2) obviously holds. It gives you an upper bound, but it is not a supremum. , but people are generally used to express the former when expressing.

In addition, a problem itself also has its complexity. If the complexity of an algorithm reaches the lower bound of the complexity of the problem, then such an algorithm is called the best algorithm.

"Big O notation": The basic parameter used in this description is n, the size of the problem instance, expressing the complexity or running time as a function of n. The "O" here represents the order. For example, "Binary search is O(logn)", which means that it needs to "retrieve an array of size n through logn steps." The notation O ( f(n) ) means that when n increases, the running time will at most increase at a rate proportional to f(n).

This asymptotic estimation is very valuable for theoretical analysis and rough comparison of algorithms, but in practice details may also cause differences. For example, an O(n2) algorithm with low overhead may run faster for small n than an O(nlogn) algorithm with high overhead. Of course, as n becomes large enough, algorithms with slower rising functions must work faster.

O(1)

##Temp=i;i=j;j=temp;                    

The above three single statements The frequency of is all 1, and the execution time of this program segment is a constant independent of the problem size n. The time complexity of the algorithm is constant order, recorded as T(n)=O(1). If the execution time of the algorithm does not increase with the increase of the problem size n, even if there are thousands of statements in the algorithm, its execution time will only be a large constant. The time complexity of this type of algorithm is O(1).

O(n^2)

2.1. Exchange the contents of i and j

sum=0; (one time)

for(i=1;ib7952b0b084dd3cabbeb279a0f42dff6left subtree->right subtree

In-order traversal: left subtree->root node->right subtree

Post-order traversal: left subtree->right subtree->root node

For example: find three traversals of the following tree

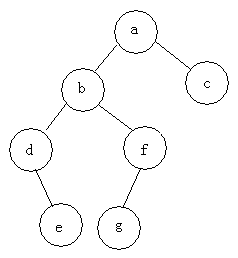
Pre-order traversal: abdefgc

In-order traversal: debgfac

Post-order traversal: edgfbca

Type of binary tree

(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

如何判断一棵树是完全二叉树？按照定义

教材上的说法：一个深度为k，节点个数为 2^k - 1 的二叉树为满二叉树。这个概念很好理解，就是一棵树，深度为k，并且没有空位。

首先对满二叉树按照广度优先遍历（从左到右）的顺序进行编号。

一颗深度为k二叉树，有n个节点，然后，也对这棵树进行编号，如果所有的编号都和满二叉树对应，那么这棵树是完全二叉树。

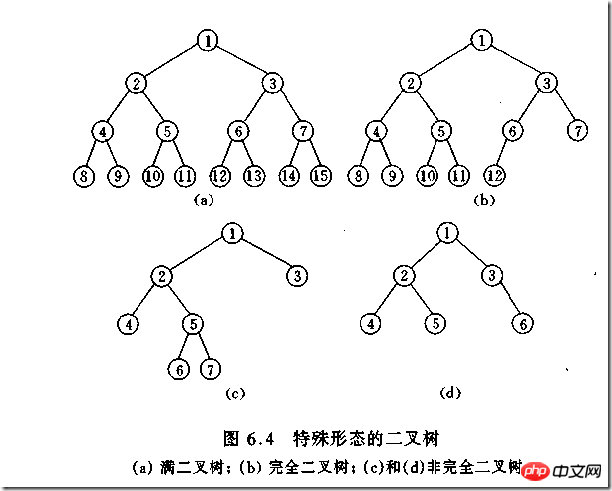
如何判断平衡二叉树？

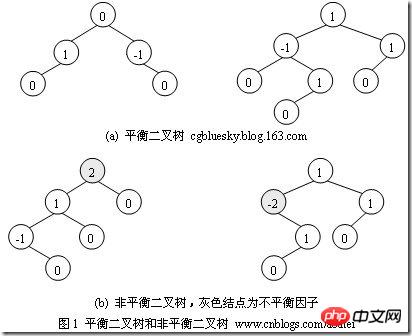
（b）左边的图 左子数的高度为3，右子树的高度为1，相差超过1

（b）右边的图 -2的左子树高度为0 右子树的高度为2，相差超过1

二叉树遍历实现

class TreeNode(object):
 def __init__(self,data=0,left=0,right=0):
 self.data = data
 self.left = left
 self.right = right
 
class BTree(object):
 def __init__(self,root=0):
 self.root = root
 
 
 def preOrder(self,treenode):
 if treenode is 0:
 return
 print(treenode.data)
 self.preOrder(treenode.left)
 self.preOrder(treenode.right)
 def inOrder(self,treenode):
 if treenode is 0:
 return
 self.inOrder(treenode.left)
 print(treenode.data)
 self.inOrder(treenode.right)
 
 def postOrder(self,treenode):
 if treenode is 0:
 return
 self.postOrder(treenode.left)
 self.postOrder(treenode.right)
 print(treenode.data)
if __name__ == '__main__':
 n1 = TreeNode(data=1)
 n2 = TreeNode(2,n1,0)
 n3 = TreeNode(3)
 n4 = TreeNode(4)
 n5 = TreeNode(5,n3,n4)
 n6 = TreeNode(6,n2,n5)
 n7 = TreeNode(7,n6,0)
 n8 = TreeNode(8)
 root = TreeNode('root',n7,n8)
 
 bt = BTree(root)
 print("preOrder".center(50,'-'))
 print(bt.preOrder(bt.root))
 
 print("inOrder".center(50,'-'))
 print (bt.inOrder(bt.root))
 
 print("postOrder".center(50,'-'))
 print (bt.postOrder(bt.root))

堆排序

堆排序，顾名思义，就是基于堆。因此先来介绍一下堆的概念。
堆分为最大堆和最小堆，其实就是完全二叉树。最大堆要求节点的元素都要大于其孩子，最小堆要求节点元素都小于其左右孩子，两者对左右孩子的大小关系不做任何要求，其实很好理解。有了上面的定义，我们可以得知，处于最大堆的根节点的元素一定是这个堆中的最大值。其实我们的堆排序算法就是抓住了堆的这一特点，每次都取堆顶的元素，将其放在序列最后面，然后将剩余的元素重新调整为最大堆，依次类推，最终得到排序的序列。

堆排序就是把堆顶的最大数取出,

将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现

剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束

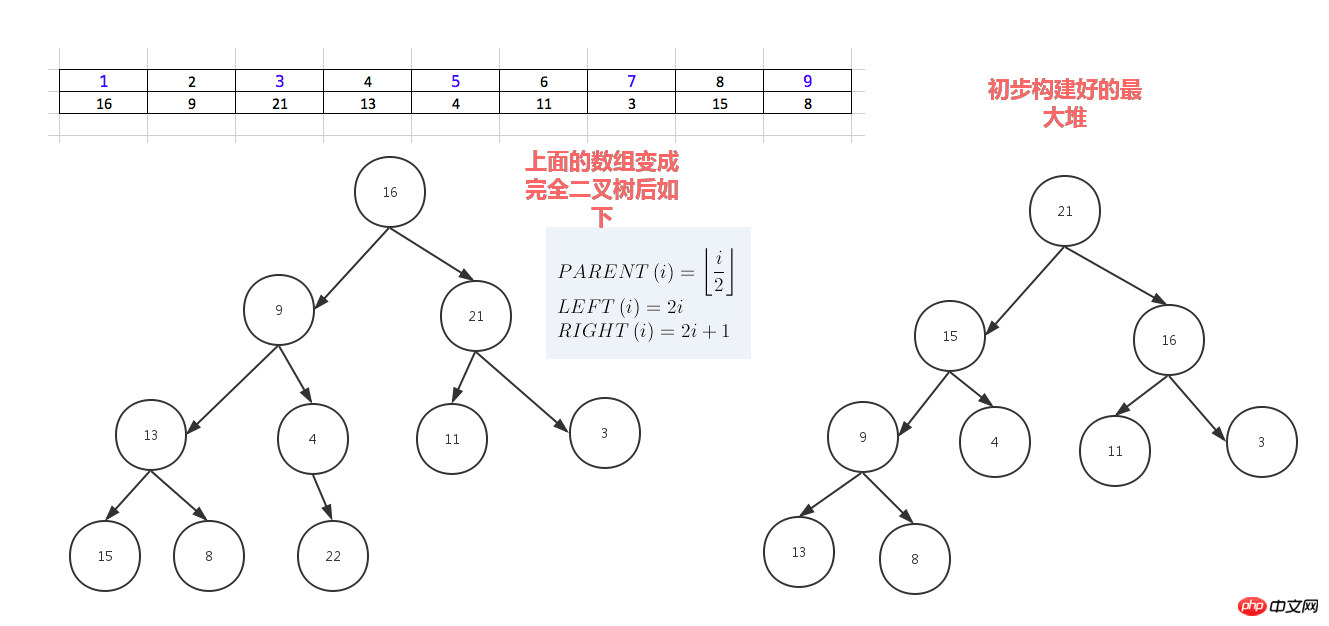
#_*_coding:utf-8_*_
__author__ = 'Alex Li'
import time,random
def sift_down(arr, node, end):
 root = node
 #print(root,2*root+1,end)
 while True:
 # 从root开始对最大堆调整
 
 child = 2 * root +1 #left child
 if child > end:
 #print('break',)
 break
 print("v:",root,arr[root],child,arr[child])
 print(arr)
 # 找出两个child中交大的一个
 if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
 child += 1 #设置右边为大
 
 if arr[root] < arr[child]:
 # 最大堆小于较大的child, 交换顺序
 tmp = arr[root]
 arr[root] = arr[child]
 arr[child]= tmp
 
 # 正在调整的节点设置为root
 #print("less1:", arr[root],arr[child],root,child)
 
 root = child #
 #[3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
 #print("less2:", arr[root],arr[child],root,child)
 else:
 # 无需调整的时候, 退出
 break
 #print(arr)
 print(&#39;-------------&#39;)
 
def heap_sort(arr):
 # 从最后一个有子节点的孩子还是调整最大堆
 first = len(arr) // 2 -1
 for i in range(first, -1, -1):
 sift_down(arr, i, len(arr) - 1)
 #[29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
 print(&#39;--------end---&#39;,arr)
 # 将最大的放到堆的最后一个, 堆-1, 继续调整排序
 for end in range(len(arr) -1, 0, -1):
 arr[0], arr[end] = arr[end], arr[0]
 sift_down(arr, 0, end - 1)
 #print(arr)
def main():
 # [7, 95, 73, 65, 60, 77, 28, 62, 43]
 # [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
 #l = [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
 #l = [16,9,21,13,4,11,3,22,8,7,15,27,0]
 array = [16,9,21,13,4,11,3,22,8,7,15,29]
 #array = []
 #for i in range(2,5000):
 # #print(i)
 # array.append(random.randrange(1,i))
 
 print(array)
 start_t = time.time()
 heap_sort(array)
 end_t = time.time()
 print("cost:",end_t -start_t)
 print(array)
 #print(l)
 #heap_sort(l)
 #print(l)
 
 
if __name__ == "__main__":
 main()

人类能理解的版本

dataset = [16,9,21,3,13,14,23,6,4,11,3,15,99,8,22]

for i in range(len(dataset)-1,0,-1):
 print("-------",dataset[0:i+1],len(dataset),i)
 #for index in range(int(len(dataset)/2),0,-1):
 for index in range(int((i+1)/2),0,-1):
 print(index)
 p_index = index

 l_child_index = p_index *2 - 1
 r_child_index = p_index *2
 print("l index",l_child_index,'r index',r_child_index)
 p_node = dataset[p_index-1]
 left_child = dataset[l_child_index]

 if p_node < left_child: # switch p_node with left child
 dataset[p_index - 1], dataset[l_child_index] = left_child, p_node
 # redefine p_node after the switch ,need call this val below
 p_node = dataset[p_index - 1]

 if r_child_index < len(dataset[0:i+1]): #avoid right out of list index range
 #if r_child_index < len(dataset[0:i]): #avoid right out of list index range
 #print(left_child)
 right_child = dataset[r_child_index]
 print(p_index,p_node,left_child,right_child)

 # if p_node < left_child: #switch p_node with left child
 # dataset[p_index - 1] , dataset[l_child_index] = left_child,p_node
 # # redefine p_node after the switch ,need call this val below
 # p_node = dataset[p_index - 1]
 #
 if p_node < right_child: #swith p_node with right child
 dataset[p_index - 1] , dataset[r_child_index] = right_child,p_node
 # redefine p_node after the switch ,need call this val below
 p_node = dataset[p_index - 1]

 else:
 print("p node [%s] has no right child" % p_node)


 #最后这个列表的第一值就是最大堆的值，把这个最大值放到列表最后一个， 把神剩余的列表再调整为最大堆

 print("switch i index", i, dataset[0], dataset[i] )
 print("before switch",dataset[0:i+1])
 dataset[0],dataset[i] = dataset[i],dataset[0]
 print(dataset)

希尔排序（shell sort）

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本,该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高

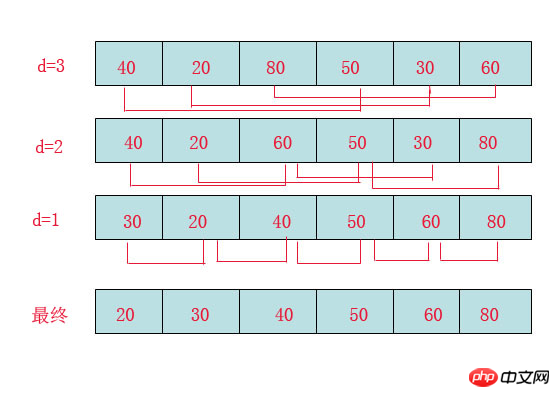
首先要明确一下增量的取法：

第一次增量的取法为： d=count/2;

第二次增量的取法为: d=(count/2)/2;

最后一直到: d=1;

看上图观测的现象为：

d=3时：将40跟50比，因50大，不交换。

              将20跟30比，因30大，不交换。

              将80跟60比，因60小，交换。

d=2时：将40跟60比，不交换，拿60跟30比交换，此时交换后的30又比前面的40小，又要将40和30交换，如上图。

              将20跟50比，不交换，继续将50跟80比，不交换。

d=1时：这时就是前面讲的插入排序了，不过此时的序列已经差不多有序了，所以给插入排序带来了很大的性能提高。

希尔排序代码

import time,random

#source = [8, 6, 4, 9, 7, 3, 2, -4, 0, -100, 99]
#source = [92, 77, 8,67, 6, 84, 55, 85, 43, 67]

source = [ random.randrange(10000+i) for i in range(10000)]
#print(source)



step = int(len(source)/2) #分组步长

t_start = time.time()


while step >0:
 print("---step ---", step)
 #对分组数据进行插入排序

 for index in range(0,len(source)):
 if index + step < len(source):
 current_val = source[index] #先记下来每次大循环走到的第几个元素的值
 if current_val > source[index+step]: #switch
 source[index], source[index+step] = source[index+step], source[index]

 step = int(step/2)
else: #把基本排序好的数据再进行一次插入排序就好了
 for index in range(1, len(source)):
 current_val = source[index] # 先记下来每次大循环走到的第几个元素的值
 position = index

 while position > 0 and source[
  position - 1] > current_val: # 当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来
 source[position] = source[position - 1] # 把左边的一个元素往右移一位
 position -= 1 # 只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止

 source[position] = current_val # 已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里
 print(source)

t_end = time.time() - t_start

print("cost:",t_end)

The above is the detailed content of Basic and commonly used algorithms in Python. For more information, please follow other related articles on the PHP Chinese website!