Use JS to implement the establishment of a binary search tree and some traversal methods

This article mainly introduces the establishment of a binary search tree implemented in JS and the implementation of some traversal methods. It has certain reference value and interested friends can refer to it.

Binary search tree is composed of nodes and edges.

We can define a node class Node, which stores the node data and the left and right sub-nodes, and then define a method for displaying the data:

//以下定义一个节点类
function Node(data,left,right){
  // 节点的键值
  this.data = data;
  // 左节点
  this.left = left;
  // 右节点
  this.right = left;
  // 显示该节点的键值
  this.show = show;
}
// 实现show方法
function show(){
  return this.data;
}

Then define a binary search tree class BST. This class defines the root node of the tree, initializes it to null, and then defines the method of inserting the node, and the method of traversing one side:

// 二叉查找树BST
// 有一个节点属性，还有一些其他的方法，以下定义一个二叉查找树BST类
function BST(){
  // 根节点初始化为空
  this.root = null;
  // 方法
  // 插入
  this.insert = insert;
  // Use JS to implement the establishment of a binary search tree and some traversal methods
  this.inorder = inorder;
  // Use JS to implement the establishment of a binary search tree and some traversal methods
  this.preorder = preorder;
  // Use JS to implement the establishment of a binary search tree and some traversal methods
  this.postorder = postorder;
}

//实现insert插入方法
function insert(data){
  // 创建一个节点保存数据
  var node = new Node(data,null,null);
  // 下面将节点node插入到树中
  // 如果树是空的，就将节点设为根节点
  if(!this.root){
    this.root = node;
  }else{ //树不为空
    // 判断插在父节点的左边还是右边
    // 所以先要保存一下父节点
    // var parent = this.root;
    var current = this.root;
    var parent;
    // 如果要插入的节点键值小于父节点键值，则插在父节点左边，
    // 前提是父节点的左边为空，否则要将父节点往下移一层，
    // 然后再做判断
    while(true){
      // data小于父节点的键值
      parent = current;
      if(data < parent.data){
        // 将父节点往左下移(插入左边)
        // parent = parent.left;
        current = current.left;
        // 如果节点为空，则直接插入
        if(!current){
          // ！！！此处特别注意，如果就这样把parent赋值为node，也仅仅只是parent指向node，
          // 而并没有加到父元素的左边！！！根本没有加到树中去。所以要先记住父元素，再把当前元素加入进去
          parent.left = node;
          break;
        }      
      }else{ // 将父节点往右下移(插入右边)
        current = current.right;
        if(!current){
          parent.right = node;
          break;
        }
      }
    }

  }
} 

//实现inorder遍历方法(左中右)
function inorder(node){
  if(node){
    inorder(node.left);
    console.log(node.show());
    inorder(node.right);
  }
}

// Use JS to implement the establishment of a binary search tree and some traversal methods(中左右)
function preorder(node){
  if(node){
    console.log(node.show());
    preorder(node.left);
    preorder(node.right);
  }
}

// Use JS to implement the establishment of a binary search tree and some traversal methods(左右中)
function postorder(node){
  if(node){
    preorder(node.left);
    preorder(node.right);
    console.log(node.show());
  }
}

Test:

// Use JS to implement the establishment of a binary search tree and some traversal methods(左右中)
function postorder(node){
  if(node){
    postorder(node.left);
    postorder(node.right);
    console.log(node.show());
  }
}

// 实例化一个BST树
var tree = new BST();
// 添加节点
tree.insert(30);
tree.insert(14);
tree.insert(35);
tree.insert(12);
tree.insert(17);
// Use JS to implement the establishment of a binary search tree and some traversal methods
tree.inorder(tree.root);
// Use JS to implement the establishment of a binary search tree and some traversal methods
tree.preorder(tree.root);
// Use JS to implement the establishment of a binary search tree and some traversal methods
tree.postorder(tree.root);

Result:

In-order traversal:

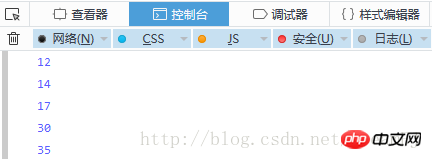
Pre-order traversal:

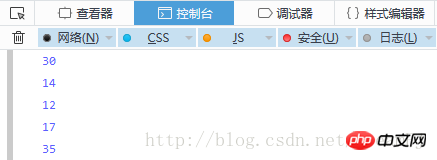
Post-order traversal:

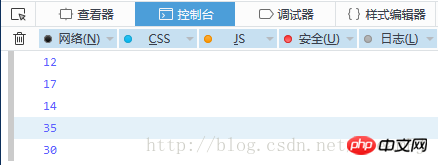
The above is the detailed content of Use JS to implement the establishment of a binary search tree and some traversal methods. For more information, please follow other related articles on the PHP Chinese website!