Home >WeChat Applet >WeChat Development >Conjecture on the implementation principle of WeChat red envelopes
Conjecture on the implementation principle of WeChat red envelopes
- 阿神Original
- 2017-02-10 14:31:162165browse
The following content comes from the background of the chat records of a high-availability architecture group at QCon: A friend consulted about the architecture of WeChat red envelopes, and the following discussion content was drawn from the explanations and discussions of official or unofficial classmates. During this period, there were many A classmate gave a red envelope to test the algorithm on the current network.
The process of grabbing red envelopes
When someone sends a red envelope to N people in the group, with a total amount of M yuan, what happens in the background is as follows:
1. Background operation for sending red envelopes:
Add a red envelope record in the database, store it in CKV, and set the expiration time;
In Cache (maybe Tencent’s internal kv database, based on memory, It has been implemented and has a kernel-state network processing module to provide services in the form of a kernel module)). Add a record to store the number of people grabbing red envelopes N
2. Backstage operation of grabbing red envelopes:
Grabbing red envelopes It is divided into grabbing and demolishing. The grabbing operation is completed at the Cache layer. The number of red envelopes is decremented through atomic subtraction operation until it reaches 0. This means that they are all robbed. In the end, the actual amount of background teardown operations is not large. Through the separation of operations, invalid requests are directly blocked outside the Cache layer. The atomic subtraction operation here is not an atomic subtraction operation in the true sense, but The CAS provided by the Cache layer keeps trying by comparing version numbers. There is a certain degree of conflict. The conflicting user will be released and allowed to proceed to the next step of disassembly. This also explains why some users grabbed the dismantling operation. The situation when development has been completed.
Opening of red envelopes is completed in the database. The number and amount received are accumulated through the transaction operation of the database, and a claim is inserted. Running water and recording are asynchronous operations, which also explains why red envelopes cannot be seen in the balance after receiving them during the Spring Festival. The amount will be calculated in real time when splitting. The amount is a random number between 1 point and 2 times the remaining average. A total amount A red envelope worth M yuan, the largest red envelope is M * 2 /N (and will not exceed M), when the red envelope is opened, the remaining amount and number will be updated. Tenpay prepares for 200,000 transactions per second, but the actual amount is only 80,000 per second.
FAQ
Since there are atoms reduced when grabbing, shouldn't there be a situation where there is no one after grabbing it and disassembling it?
The atomic subtraction here is not an atomic operation in the true sense. It is the CAS provided by the Cache layer. It tries continuously by comparing the version numbers.
What should I do if the cache and db are down?
Main and backup + reconciliation
Is there any red envelope that has been lost, but the balance is still there?
No, the program will have a take all operation and an asynchronous reconciliation guarantee at the end.
Why do we need to separate grabbing and demolition?
The general idea is to set up multi-layer filters, filter layer by layer, and reduce flow and pressure layer by layer. This design was originally because the grabbing operation is the business layer, and the splitting operation is the accounting operation. One operation is too heavy, and the interruption rate is high. From the interface level, the first interface is a pure cache operation and has strong compression capabilities. A simple query Cache blocks most users and performs the first filtering, so most people will see a prompt that the content has been sold out.
After grabbing the red envelope, send it out or withdraw cash. Is there any strategy here?
Large amount priority deposit strategy
Is there any data to prove whether the probability of each red envelope is equal?
It’s not absolutely equal, it’s just a simple brain-patting algorithm.
With the head-patting algorithm, will there be two best ones?
There will be the same amount, but there is only one lucky one, the one who grabs it first is the best.
Will the money of the person who sends the red envelope be frozen?
It is deducted directly in real time, not frozen.
What are the reasons for calculating the amount in real time?
Real-time efficiency is higher, but budget efficiency is low. The budget also accounts for additional storage. Because the red envelope only occupies one record and is valid for only a few days, it does not require much space. Even when the pressure is high, the horizontal expansion machine is.
Test 2: Zhihu user "Ma Jingcheng"'s experiment:
Here is a survey sample data of 100 samples, and put forward your own guess.
1. The wallet money satisfies the censored normal random number distribution. Roughly speaking, random numbers are taken from a censored normal distribution, and the summed number is divided by the total value to obtain the correction factor, and then the correction factor is multiplied by all the random numbers to obtain the red envelope value.
This distribution means: there are more red envelopes below the average, but not far from the average; there are few red envelopes above the average, but there are more red envelopes that are much larger than the average.
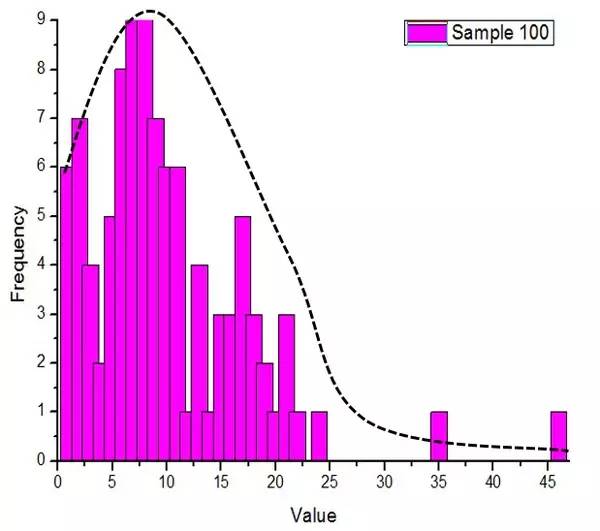
Figure 1. Wallet value and its frequency distribution histogram and its normal fitting
But looking at the distribution histogram does not infer that it conforms to the normal distribution , but considering the simplicity of the program and the rationality of the random numbers, this is the most reasonable guess.
2. The wallets at the back are generally more valuable
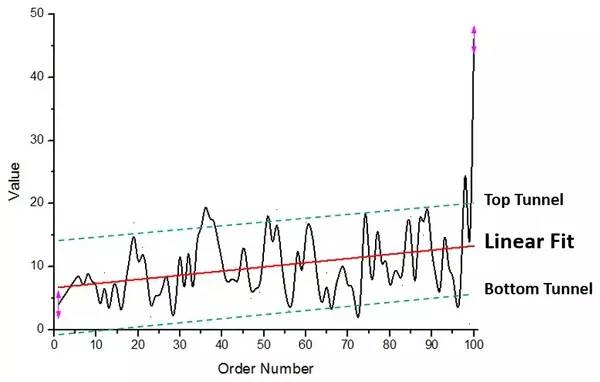
Figure 2. The relationship between the wallet serial number and its value
It can be seen from the linear fitting red line in Figure 2 that the overall change trend of wallet value is slowly increasing, and its change range is approximately a "channel" delineated by the upper and lower bounds of the green dotted line. (The curve can be enclosed in such a regular "channel", which also reflects the rationality of Rule 1 from the side and illustrates that random numbers are not uniformly distributed)
From another average This pattern can also be seen in the figure.
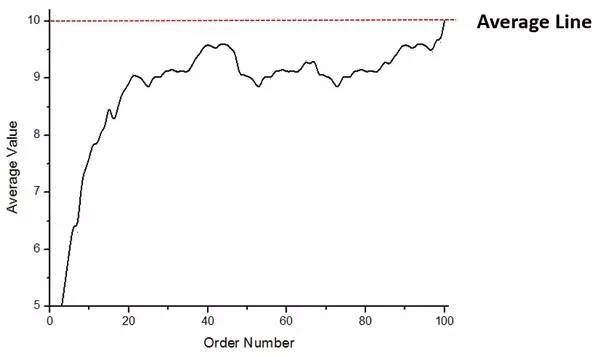
Figure 3. Change curve of average number with sequence number
In the sample, a wallet worth 1,000 was Divided into 100 parts, the mean is 10. However, in Figure 3 we can see that before the last wallet, the average has been lower than 10, which shows that the value of the wallet at the beginning is low, and has been pulled upward by the value of the wallet in the later period. The value is higher.
3. Of course, the average graph can also reveal another rule, that is, the last person is often lucky enough to draw more. Because the last person gets whatever is left in their wallet, and the average of everyone before is less than 10, it is at least guaranteed that the last person will be higher than the average. In this sample, wallet number 98 drew 35, while the last wallet drew 46.
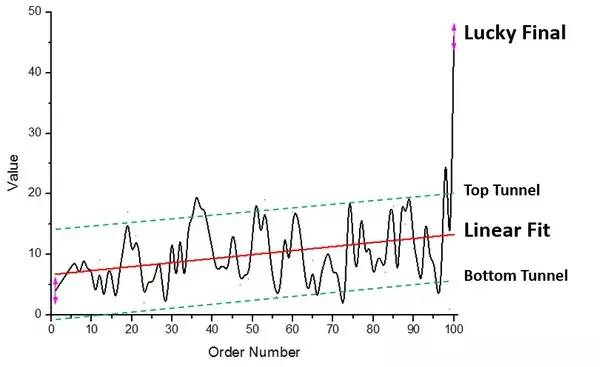
In summary, based on the sample guess:
1. Most of the time, the money drawn is as small as others, but once it is more, it will be much easier a lot of.
2. The more you pull out the wallet at the back, the easier it is to make money.
3. The last person is often lucky.
Related articles
See more- Detailed explanation and simple usage of WeChat mini program textarea
- PHP WeChat public account development (2) Baidu BAE construction and database use
- php WeChat public account development (3) php implements simple WeChat text communication
- php WeChat public account development (4) php implements custom keyword reply
- PHP version of WeChat store calling api sample code

