Home >Backend Development >PHP Tutorial >Detailed explanation of the data structure and algorithm principles behind MySQL indexes
Detailed explanation of the data structure and algorithm principles behind MySQL indexes
- 高洛峰Original
- 2017-01-16 15:12:231167browse
Abstract
This article takes the MySQL database as the research object and discusses some topics related to database indexes. It should be noted that MySQL supports many storage engines, and various storage engines have different support for indexes. Therefore, the MySQL database supports multiple index types, such as BTree index, hash index, full-text index, etc. In order to avoid confusion, this article will only focus on the BTree index, because this is the index that is mainly dealt with when using MySQL. As for the hash index and full-text index, this article will not discuss it for the time being.
The main content of the article is divided into three parts.
The first part mainly discusses the mathematical basis of MySQL database index from the theoretical level of data structure and algorithm.
The second part discusses topics such as clustered indexes, non-clustered indexes and covering indexes based on the architecture implementation of indexes in the MyISAM and InnoDB data storage engines in the MySQL database.
The third part discusses the strategy of high-performance index use in MySQL based on the above theoretical basis.
Basics of data structure and algorithm
The essence of index
MySQL’s official definition of index is: Index (Index) is a data structure that helps MySQL obtain data efficiently. By extracting the backbone of the sentence, you can get the essence of the index: the index is a data structure.
We know that database query is one of the most important functions of the database. We all want to query data as fast as possible, so designers of database systems will optimize from the perspective of query algorithms. The most basic query algorithm is of course linear search. This algorithm with a complexity of O(n) is obviously bad when the amount of data is large. Fortunately, the development of computer science has provided many better search algorithms. , such as binary search, binary tree search, etc. If you do a little analysis, you will find that each search algorithm can only be applied to a specific data structure. For example, binary search requires that the retrieved data be ordered, while binary tree search can only be applied to binary search trees, but the data itself The organizational structure cannot completely satisfy various data structures (for example, it is theoretically impossible to organize both columns in order at the same time), so in addition to the data, the database system also maintains data structures that satisfy specific search algorithms. Structures reference (point to) data in some way, allowing advanced search algorithms to be implemented on these data structures. This data structure is an index.
Look at an example:
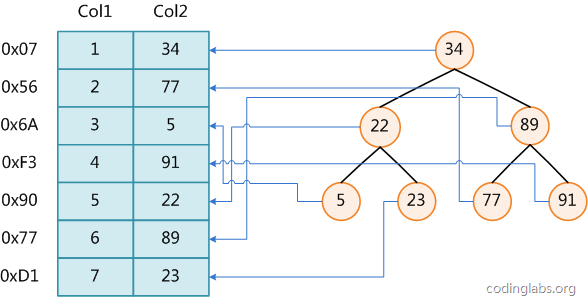
Figure 1
Figure 1 shows a possible indexing method. On the left is a data table with a total of two columns and seven records. The leftmost one is the physical address of the data record (note that logically adjacent records are not necessarily physically adjacent on the disk). In order to speed up the search of Col2, you can maintain a binary search tree as shown on the right. Each node contains the index key value and a pointer to the physical address of the corresponding data record. In this way, you can use binary search in O(log2n) The corresponding data is obtained within the complexity.
Although this is a genuine index, actual database systems are almost never implemented using binary search trees or their evolved varieties, red-black trees. The reasons will be introduced below.
B-Tree and B+Tree
Currently, most database systems and file systems use B-Tree or its variant B+Tree as the index structure, which will be combined in the next section of this article. Memory principles and computer access principles discuss why B-Tree and B+Tree are so widely used in indexes. This section first describes them purely from the perspective of data structure.
B-Tree
In order to describe B-Tree, first define a data record as a tuple [key, data], key is the key value of the record, for different data records, key They are different from each other; data is the data record except key. Then B-Tree is a data structure that meets the following conditions:
1. d is a positive integer greater than 1, which is called the degree of B-Tree.
2. h is a positive integer, called the height of B-Tree.
3. Each non-leaf node consists of n-1 keys and n pointers, where d
4. Each leaf node contains at least one key and two pointers, and at most 2d-1 keys and 2d pointers. The pointers of leaf nodes are all null.
5. All leaf nodes have the same depth, which is equal to the tree height h.
6. The key and pointer are spaced apart from each other, and the two ends of the node are pointers.
7. The keys in a node are arranged non-decreasingly from left to right.
8. All nodes form a tree structure.
9. Each pointer is either null or points to another node.
10. If a pointer is on the leftmost side of a node and is not null, then all the keys it points to are less than v(key1), where v(key1) is the value of the first key of the node.
11. If a pointer is on the rightmost side of a node and is not null, then all the keys it points to are greater than v(keym), where v(keym) is the value of the last key of the node.
12. If a pointer’s left and right adjacent keys of a node are keyi and keyi+1 respectively and are not null, then all keys pointing to the node are less than v(keyi+1) and greater than v( keyi).
Figure 2 is a schematic diagram of a B-Tree with d=2.
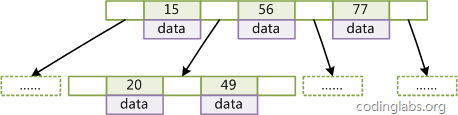
Figure 2
Due to the characteristics of B-Tree, the algorithm for retrieving data by key in B-Tree is very intuitive: first perform a binary search from the root node, if If found, the data of the corresponding node will be returned. Otherwise, the node pointed to by the pointer of the corresponding interval will be searched recursively until the node is found or the null pointer is found. The former search is successful and the latter search fails. The pseudocode of the search algorithm on B-Tree is as follows:
BTree_Search(node, key)
{
if(node == null) return null;
foreach(node.key)
{
if(node.key[i] == key) return node.data[i];
if(node.key[i] > key) return BTree_Search(point[i]->node);
}
return BTree_Search(point[i+1]->node);
}
data = BTree_Search(root, my_key);There are a series of interesting properties about B-Tree. For example, if a B-Tree with degree d has N keys as its index, then its tree height will be h The upper limit of is logd((N+1)/2). To retrieve a key, the asymptotic complexity of finding the number of nodes is O(logdN). It can be seen from this point that B-Tree is a very efficient index data structure.
In addition, since inserting and deleting new data records will destroy the properties of B-Tree, when inserting and deleting, the tree needs to be split, merged, transferred, etc. to maintain the properties of B-Tree. This article does not I plan to discuss the contents of B-Tree in full, because there are already many materials that detail the mathematical properties and insertion and deletion algorithms of B-Tree. Interested friends can find the corresponding materials in the reference column at the end of this article to read.
B+Tree
There are many variations of B-Tree, the most common of which is B+Tree. For example, MySQL generally uses B+Tree to implement its index structure.
Compared with B-Tree, B+Tree has the following differences:
1. The upper limit of the pointer of each node is 2d instead of 2d+1.
2. Internal nodes do not store data, only keys; leaf nodes do not store pointers.
Figure 3 is a simple B+Tree diagram.
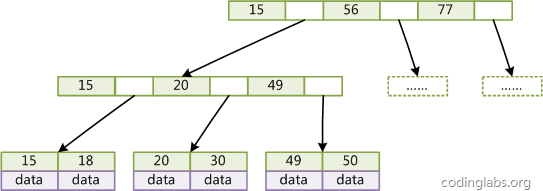
Figure 3
Since not all nodes have the same domain, leaf nodes and internal nodes in B+Tree generally have different sizes. This is different from B-Tree. Although the number of keys and pointers stored in different nodes in B-Tree may be inconsistent, the domain and upper limit of each node are consistent. Therefore, in implementation, B-Tree often applies equally to each node. size of space.
Generally speaking, B+Tree is more suitable for implementing external storage index structures than B-Tree. The specific reasons are related to the principles of external memory and computer access, which will be discussed below.
B+Tree with sequential access pointers
The B+Tree structure generally used in database systems or file systems has been optimized on the basis of the classic B+Tree, adding Sequentially access pointers.
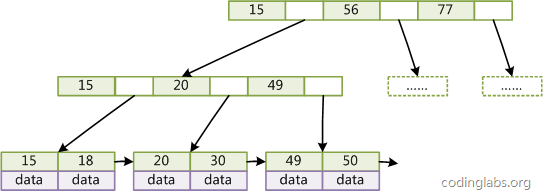
Figure 4
As shown in Figure 4, add a pointer to the adjacent leaf node in each leaf node of B+Tree to form A B+Tree with sequential access pointers. The purpose of this optimization is to improve the performance of interval access. For example, in Figure 4, if you want to query all data records with keys from 18 to 49, after finding 18, you only need to traverse the nodes and pointers sequentially to access them all at once. to all data nodes, greatly improving the efficiency of interval query.
This section gives a brief introduction to B-Tree and B+Tree. The next section combines the principles of memory access to introduce why B+Tree is currently the preferred data structure for indexing in database systems.
Why use B-Tree (B+Tree)
As mentioned above, data structures such as red-black trees can also be used to implement indexes, but file systems and database systems generally use B- /+Tree is used as an index structure. This section will discuss the theoretical basis of B-/+Tree as an index based on knowledge about computer composition principles.
Generally speaking, the index itself is also very large and cannot be stored entirely in memory, so the index is often stored on disk in the form of an index file. In this case, disk I/O consumption will be generated during the index search process. Compared with memory access, the consumption of I/O access is several orders of magnitude higher. Therefore, the most important indicator to evaluate the quality of a data structure as an index is The asymptotic complexity of the number of disk I/O operations during the search process. In other words, the structural organization of the index should minimize the number of disk I/O accesses during the search process. The following will first introduce the principles of memory and disk access, and then combine these principles to analyze the efficiency of B-/+Tree as an index.
Main memory access principle
The main memory currently used in computers is basically random read-write memory (RAM). The structure and access principle of modern RAM are relatively complex. This article will ignore the specific differences. , abstracting a very simple access model to illustrate the working principle of RAM.
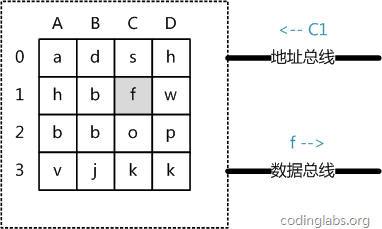
Figure 5
From an abstract point of view, main memory is a matrix composed of a series of storage units, each storage unit stores fixed-size data. Each storage unit has a unique address. The addressing rules of modern main memory are relatively complex. Here they are simplified into a two-dimensional address: a storage unit can be uniquely located through a row address and a column address. Figure 5 shows a 4 x 4 main memory model.
The main memory access process is as follows:
When the system needs to read the main memory, the address signal is put on the address bus and passed to the main memory. After the main memory reads the address signal, Analyze the signal and locate the specified storage unit, and then put the data of this storage unit on the data bus for other components to read.
The process of writing to main memory is similar. The system places the unit address and data to be written on the address bus and data bus respectively. The main memory reads the contents of the two buses and performs corresponding write operations.
It can be seen here that the time of main memory access is only linearly related to the number of accesses. Because there is no mechanical operation, the "distance" of the data accessed twice will not have any impact on the time. For example, the time consumption of taking A0 first and then A1 is the same as taking A0 first and then D3.
Disk access principle
As mentioned above, indexes are generally stored on disk in the form of files, and index retrieval requires disk I/O operations. Unlike main memory, disk I/O involves mechanical movement costs, so the time consumption of disk I/O is huge.
Figure 6 is a schematic diagram of the overall structure of the disk.
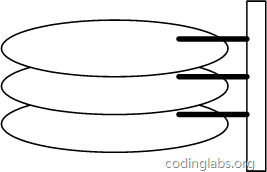
Figure 6
A disk is composed of circular disks of the same size and coaxiality. The disks can rotate (each disk must rotate synchronously). There is a head bracket on one side of the disk. The head bracket fixes a set of heads. Each head is responsible for accessing the contents of a disk. The magnetic head cannot rotate, but it can move along the radius of the disk (actually oblique tangential movement). Each magnetic head must also be coaxial at the same time, that is, when viewed from directly above, all magnetic heads overlap at any time (but At present, there is multi-head independent technology, which is not subject to this restriction).
Figure 7 is a schematic diagram of the disk structure.
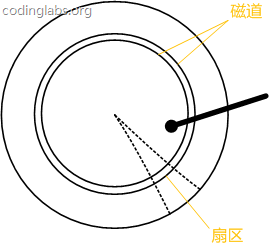
Figure 7
The disc is divided into a series of concentric rings. The center of the circle is the center of the disc. Each concentric ring is called a track. All the concentric rings have the same radius. The tracks form a cylinder. The track is divided into small segments along the radius line. Each segment is called a sector, and each sector is the smallest storage unit of the disk. For the sake of simplicity, we assume below that the disk has only one platter and one head.
When data needs to be read from the disk, the system will transfer the logical address of the data to the disk. The control circuit of the disk will translate the logical address into a physical address according to the addressing logic, that is, determine which track the data to be read is on. , which sector. In order to read the data in this sector, the magnetic head needs to be placed over this sector. In order to achieve this, the magnetic head needs to move to align with the corresponding track. This process is called seek, and the time spent is called seek time. Then the disk rotation will The target sector is rotated under the head. The time spent in this process is called rotation time.
Locality principle and disk read-ahead
Due to the characteristics of the storage medium, disk access is much slower than main memory. Coupled with the cost of mechanical movement, the disk access speed is often One hundredth of the main memory, so in order to improve efficiency, disk I/O should be minimized. In order to achieve this goal, the disk often does not read strictly on demand, but reads in advance every time. Even if only one byte is needed, the disk will start from this position and sequentially read a certain length of data backwards into the memory. The theoretical basis for doing this is the famous locality principle in computer science:
When a piece of data is used, the data nearby is usually used immediately.
The data required during program running is usually concentrated.
Because disk sequential reading is very efficient (no seek time required, only little rotation time), read-ahead can improve I/O efficiency for programs with locality.
The read-ahead length is generally an integral multiple of the page. Pages are logical blocks of computer-managed memory. Hardware and operating systems often divide main memory and disk storage areas into consecutive equal-sized blocks. Each storage block is called a page (in many operating systems, the page size is usually 4k), main memory and disk exchange data in units of pages. When the data to be read by the program is not in the main memory, a page fault exception will be triggered. At this time, the system will send a read signal to the disk, and the disk will find the starting position of the data and read one or more pages backwards. Load into memory, then return abnormally, and the program continues to run.
Performance analysis of B-/+Tree index
At this point we can finally analyze the performance of B-/+Tree index.
As mentioned above, disk I/O times are generally used to evaluate the quality of the index structure. Let’s start with the B-Tree analysis. According to the definition of B-Tree, it can be seen that a maximum of h nodes need to be visited for one retrieval. The designers of the database system cleverly took advantage of the disk read-ahead principle and set the size of a node to be equal to one page, so that each node can be fully loaded with only one I/O. In order to achieve this goal, the following techniques need to be used in the actual implementation of B-Tree:
Every time a new node is created, a page of space is directly applied for, thus ensuring that a node is physically stored in a page. In addition, computer storage allocation is page-aligned, which means that only one I/O is required for a node.
A retrieval in B-Tree requires at most h-1 I/O (the root node is resident in memory), and the asymptotic complexity is O(h)=O(logdN). In general practical applications, the out-degree d is a very large number, usually more than 100, so h is very small (usually no more than 3).
In summary, using B-Tree as an index structure is very efficient.
As for the red-black tree structure, h is obviously much deeper. Since nodes (parents and children) that are logically close may be physically far away and locality cannot be exploited, the I/O asymptotic complexity of the red-black tree is also O(h), and the efficiency is obviously much worse than that of the B-Tree.
As mentioned above, B+Tree is more suitable for external memory indexes, and the reason is related to the out-degree d of the internal node. From the above analysis, we can see that the larger d, the better the performance of the index, and the upper limit of the out-degree depends on the size of the key and data in the node:
dmax = floor(pagesize / (keysize + datasize + pointsize) ) (pagesize – dmax >= pointsize)
or
dmax = floor(pagesize / (keysize + datasize + pointsize)) – 1 (pagesize – dmax
floor means rounding down. Since the data domain is removed from the nodes in B+Tree, they can have larger out-degrees and better performance.
This chapter discusses the data structure and algorithm issues related to indexes from a theoretical perspective. The next chapter will discuss how B+Tree is specifically implemented as an index in MySQL, and will also introduce the MyISAM and InnDB storage engines. There are two different index implementation forms: non-clustered index and clustered index.
MySQL index implementation
In MySQL, indexes are storage engine level concepts. Different storage engines implement indexes in different ways. This article mainly discusses the two storage engines MyISAM and InnoDB. Index implementation.
MyISAM index implementation
The MyISAM engine uses B+Tree as the index structure, and the data field of the leaf node stores the address of the data record. The following figure is the schematic diagram of the MyISAM index:
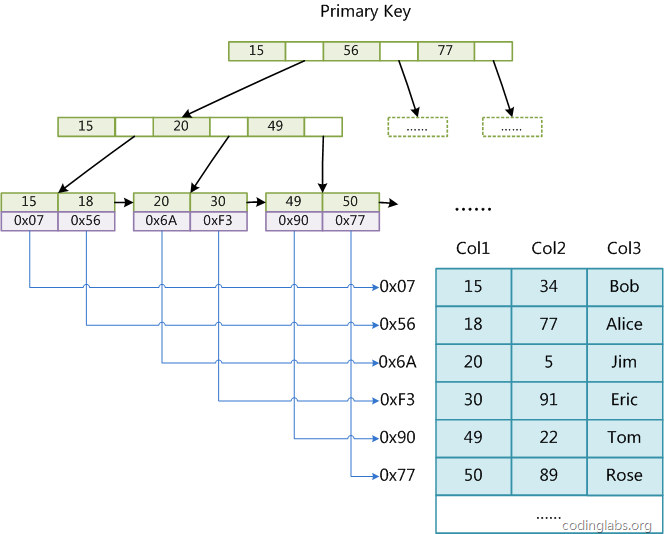
Figure 8
Assume that the table has three columns in total. Assume that we use Col1 as the primary key, then Figure 8 It is the primary index (Primary key) representation of a MyISAM table. It can be seen that MyISAM's index file only saves the address of the data record. In MyISAM, there is no structural difference between the primary index and the secondary index (Secondary key), except that the primary index requires the key to be unique, while the key of the secondary index can be repeated. If we create an auxiliary index on Col2, the structure of this index is as shown below:
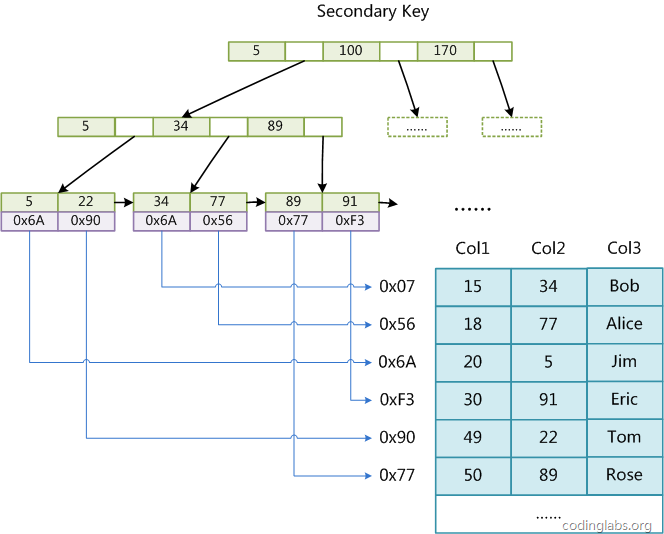
Figure 9
is also a B+Tree , the data field saves the address of the data record. Therefore, the index retrieval algorithm in MyISAM is to first search the index according to the B+Tree search algorithm. If the specified Key exists, the value of its data field is taken out, and then the value of the data field is used as the address to read the corresponding data record.
MyISAM's indexing method is also called "non-clustered". The reason why it is called so is to distinguish it from InnoDB's clustered index.
InnoDB index implementation
Although InnoDB also uses B+Tree as the index structure, the specific implementation method is completely different from MyISAM.
The first major difference is that InnoDB's data files themselves are index files. As we know from the above, the MyISAM index file and data file are separated, and the index file only saves the address of the data record. In InnoDB, the table data file itself is an index structure organized by B+Tree, and the leaf node data field of this tree saves complete data records. The key of this index is the primary key of the data table, so the InnoDB table data file itself is the primary index.
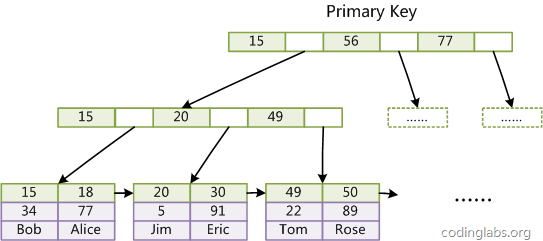
Picture 10
图10是InnoDB主索引(同时也是数据文件)的示意图,可以看到叶节点包含了完整的数据记录。这种索引叫做聚集索引。因为InnoDB的数据文件本身要按主键聚集,所以InnoDB要求表必须有主键(MyISAM可以没有),如果没有显式指定,则MySQL系统会自动选择一个可以唯一标识数据记录的列作为主键,如果不存在这种列,则MySQL自动为InnoDB表生成一个隐含字段作为主键,这个字段长度为6个字节,类型为长整形。
第二个与MyISAM索引的不同是InnoDB的辅助索引data域存储相应记录主键的值而不是地址。换句话说,InnoDB的所有辅助索引都引用主键作为data域。例如,图11为定义在Col3上的一个辅助索引:
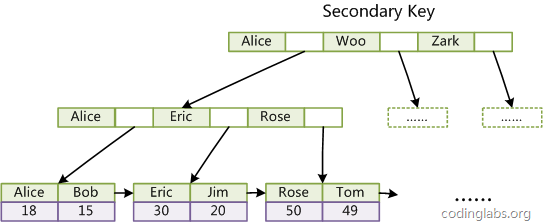
图11
这里以英文字符的ASCII码作为比较准则。聚集索引这种实现方式使得按主键的搜索十分高效,但是辅助索引搜索需要检索两遍索引:首先检索辅助索引获得主键,然后用主键到主索引中检索获得记录。
了解不同存储引擎的索引实现方式对于正确使用和优化索引都非常有帮助,例如知道了InnoDB的索引实现后,就很容易明白为什么不建议使用过长的字段作为主键,因为所有辅助索引都引用主索引,过长的主索引会令辅助索引变得过大。再例如,用非单调的字段作为主键在InnoDB中不是个好主意,因为InnoDB数据文件本身是一颗B+Tree,非单调的主键会造成在插入新记录时数据文件为了维持B+Tree的特性而频繁的分裂调整,十分低效,而使用自增字段作为主键则是一个很好的选择。
下一章将具体讨论这些与索引有关的优化策略。
索引使用策略及优化
MySQL的优化主要分为结构优化(Scheme optimization)和查询优化(Query optimization)。本章讨论的高性能索引策略主要属于结构优化范畴。本章的内容完全基于上文的理论基础,实际上一旦理解了索引背后的机制,那么选择高性能的策略就变成了纯粹的推理,并且可以理解这些策略背后的逻辑。
示例数据库
为了讨论索引策略,需要一个数据量不算小的数据库作为示例。本文选用MySQL官方文档中提供的示例数据库之一:employees。这个数据库关系复杂度适中,且数据量较大。下图是这个数据库的E-R关系图(引用自MySQL官方手册):
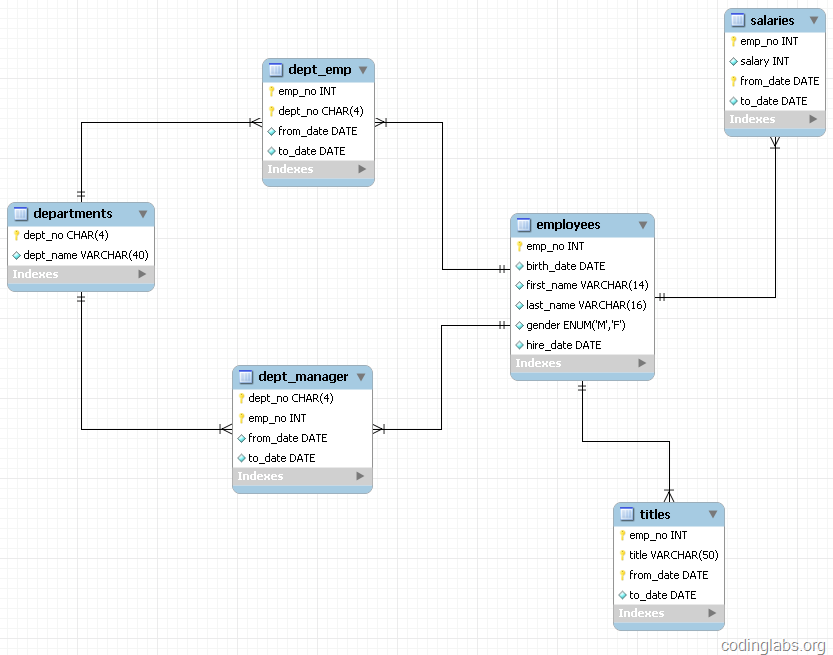
图12
MySQL官方文档中关于此数据库的页面为http://dev.mysql.com/doc/employee/en/employee.html。里面详细介绍了此数据库,并提供了下载地址和导入方法,如果有兴趣导入此数据库到自己的MySQL可以参考文中内容。
最左前缀原理与相关优化
高效使用索引的首要条件是知道什么样的查询会使用到索引,这个问题和B+Tree中的“最左前缀原理”有关,下面通过例子说明最左前缀原理。
这里先说一下联合索引的概念。在上文中,我们都是假设索引只引用了单个的列,实际上,MySQL中的索引可以以一定顺序引用多个列,这种索引叫做联合索引,一般的,一个联合索引是一个有序元组
以employees.titles表为例,下面先查看其上都有哪些索引:
SHOW INDEX FROM employees.titles; +--------+------------+----------+--------------+-------------+-----------+-------------+------+------------+ | Table | Non_unique | Key_name | Seq_in_index | Column_name | Collation | Cardinality | Null | Index_type | +--------+------------+----------+--------------+-------------+-----------+-------------+------+------------+ | titles | 0 | PRIMARY | 1 | emp_no | A | NULL | | BTREE | | titles | 0 | PRIMARY | 2 | title | A | NULL | | BTREE | | titles | 0 | PRIMARY | 3 | from_date | A | 443308 | | BTREE | | titles | 1 | emp_no | 1 | emp_no | A | 443308 | | BTREE | +--------+------------+----------+--------------+-------------+-----------+-------------+------+------------+
从结果中可以到titles表的主索引为
ALTER TABLE employees.titles DROP INDEX emp_no;
这样就可以专心分析索引PRIMARY的行为了。
情况一:全列匹配。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND title='Senior Engineer' AND from_date='1986-06-26'; +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+ | 1 | SIMPLE | titles | const | PRIMARY | PRIMARY | 59 | const,const,const | 1 | | +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+
很明显,当按照索引中所有列进行精确匹配(这里精确匹配指“=”或“IN”匹配)时,索引可以被用到。这里有一点需要注意,理论上索引对顺序是敏感的,但是由于MySQL的查询优化器会自动调整where子句的条件顺序以使用适合的索引,例如我们将where中的条件顺序颠倒:
EXPLAIN SELECT * FROM employees.titles WHERE from_date='1986-06-26' AND emp_no='10001' AND title='Senior Engineer'; +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+ | 1 | SIMPLE | titles | const | PRIMARY | PRIMARY | 59 | const,const,const | 1 | | +----+-------------+--------+-------+---------------+---------+---------+-------------------+------+-------+
效果是一样的。
情况二:最左前缀匹配。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001'; +----+-------------+--------+------+---------------+---------+---------+-------+------+-------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------+ | 1 | SIMPLE | titles | ref | PRIMARY | PRIMARY | 4 | const | 1 | | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------+
当查询条件精确匹配索引的左边连续一个或几个列时,如
情况三:查询条件用到了索引中列的精确匹配,但是中间某个条件未提供。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND from_date='1986-06-26'; +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+ | 1 | SIMPLE | titles | ref | PRIMARY | PRIMARY | 4 | const | 1 | Using where | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+
此时索引使用情况和情况二相同,因为title未提供,所以查询只用到了索引的第一列,而后面的from_date虽然也在索引中,但是由于title不存在而无法和左前缀连接,因此需要对结果进行扫描过滤from_date(这里由于emp_no唯一,所以不存在扫描)。如果想让from_date也使用索引而不是where过滤,可以增加一个辅助索引
首先我们看下title一共有几种不同的值:
SELECT DISTINCT(title) FROM employees.titles; +--------------------+ | title | +--------------------+ | Senior Engineer | | Staff | | Engineer | | Senior Staff | | Assistant Engineer | | Technique Leader | | Manager | +--------------------+
只有7种。在这种成为“坑”的列值比较少的情况下,可以考虑用“IN”来填补这个“坑”从而形成最左前缀:
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND title IN ('Senior Engineer', 'Staff', 'Engineer', 'Senior Staff', 'Assistant Engineer', 'Technique Leader', 'Manager') AND from_date='1986-06-26'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 59 | NULL | 7 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
这次key_len为59,说明索引被用全了,但是从type和rows看出IN实际上执行了一个range查询,这里检查了7个key。看下两种查询的性能比较:
SHOW PROFILES; +----------+------------+-------------------------------------------------------------------------------+ | Query_ID | Duration | Query | +----------+------------+-------------------------------------------------------------------------------+ | 10 | 0.00058000 | SELECT * FROM employees.titles WHERE emp_no='10001' AND from_date='1986-06-26'| | 11 | 0.00052500 | SELECT * FROM employees.titles WHERE emp_no='10001' AND title IN ... | +----------+------------+-------------------------------------------------------------------------------+
“填坑”后性能提升了一点。如果经过emp_no筛选后余下很多数据,则后者性能优势会更加明显。当然,如果title的值很多,用填坑就不合适了,必须建立辅助索引。
情况四:查询条件没有指定索引第一列。
EXPLAIN SELECT * FROM employees.titles WHERE from_date='1986-06-26'; +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+ | 1 | SIMPLE | titles | ALL | NULL | NULL | NULL | NULL | 443308 | Using where | +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+
由于不是最左前缀,索引这样的查询显然用不到索引。
情况五:匹配某列的前缀字符串。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND title LIKE 'Senior%'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 56 | NULL | 1 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
此时可以用到索引,但是如果通配符不是只出现在末尾,则无法使用索引。(原文表述有误,如果通配符%不出现在开头,则可以用到索引,但根据具体情况不同可能只会用其中一个前缀)
情况六:范围查询。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no < '10010' and title='Senior Engineer'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 4 | NULL | 16 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
范围列可以用到索引(必须是最左前缀),但是范围列后面的列无法用到索引。同时,索引最多用于一个范围列,因此如果查询条件中有两个范围列则无法全用到索引。
EXPLAIN SELECT * FROM employees.titles WHERE emp_no < 10010' AND title='Senior Engineer' AND from_date BETWEEN '1986-01-01' AND '1986-12-31'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 4 | NULL | 16 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
可以看到索引对第二个范围索引无能为力。这里特别要说明MySQL一个有意思的地方,那就是仅用explain可能无法区分范围索引和多值匹配,因为在type中这两者都显示为range。同时,用了“between”并不意味着就是范围查询,例如下面的查询:
EXPLAIN SELECT * FROM employees.titles WHERE emp_no BETWEEN '10001' AND '10010' AND title='Senior Engineer' AND from_date BETWEEN '1986-01-01' AND '1986-12-31'; +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+ | 1 | SIMPLE | titles | range | PRIMARY | PRIMARY | 59 | NULL | 16 | Using where | +----+-------------+--------+-------+---------------+---------+---------+------+------+-------------+
看起来是用了两个范围查询,但作用于emp_no上的“BETWEEN”实际上相当于“IN”,也就是说emp_no实际是多值精确匹配。可以看到这个查询用到了索引全部三个列。因此在MySQL中要谨慎地区分多值匹配和范围匹配,否则会对MySQL的行为产生困惑。
情况七:查询条件中含有函数或表达式。
很不幸,如果查询条件中含有函数或表达式,则MySQL不会为这列使用索引(虽然某些在数学意义上可以使用)。例如:
EXPLAIN SELECT * FROM employees.titles WHERE emp_no='10001' AND left(title, 6)='Senior'; +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+ | 1 | SIMPLE | titles | ref | PRIMARY | PRIMARY | 4 | const | 1 | Using where | +----+-------------+--------+------+---------------+---------+---------+-------+------+-------------+
虽然这个查询和情况五中功能相同,但是由于使用了函数left,则无法为title列应用索引,而情况五中用LIKE则可以。再如:
EXPLAIN SELECT * FROM employees.titles WHERE emp_no - 1='10000'; +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+ | 1 | SIMPLE | titles | ALL | NULL | NULL | NULL | NULL | 443308 | Using where | +----+-------------+--------+------+---------------+------+---------+------+--------+-------------+
显然这个查询等价于查询emp_no为10001的函数,但是由于查询条件是一个表达式,MySQL无法为其使用索引。看来MySQL还没有智能到自动优化常量表达式的程度,因此在写查询语句时尽量避免表达式出现在查询中,而是先手工私下代数运算,转换为无表达式的查询语句。
索引选择性与前缀索引
既然索引可以加快查询速度,那么是不是只要是查询语句需要,就建上索引?答案是否定的。因为索引虽然加快了查询速度,但索引也是有代价的:索引文件本身要消耗存储空间,同时索引会加重插入、删除和修改记录时的负担,另外,MySQL在运行时也要消耗资源维护索引,因此索引并不是越多越好。一般两种情况下不建议建索引。
第一种情况是表记录比较少,例如一两千条甚至只有几百条记录的表,没必要建索引,让查询做全表扫描就好了。至于多少条记录才算多,这个个人有个人的看法,我个人的经验是以2000作为分界线,记录数不超过 2000可以考虑不建索引,超过2000条可以酌情考虑索引。
另一种不建议建索引的情况是索引的选择性较低。所谓索引的选择性(Selectivity),是指不重复的索引值(也叫基数,Cardinality)与表记录数(#T)的比值:
Index Selectivity = Cardinality / #T
显然选择性的取值范围为(0, 1],选择性越高的索引价值越大,这是由B+Tree的性质决定的。例如,上文用到的employees.titles表,如果title字段经常被单独查询,是否需要建索引,我们看一下它的选择性:
SELECT count(DISTINCT(title))/count(*) AS Selectivity FROM employees.titles; +-------------+ | Selectivity | +-------------+ | 0.0000 | +-------------+
title的选择性不足0.0001(精确值为0.00001579),所以实在没有什么必要为其单独建索引。
有一种与索引选择性有关的索引优化策略叫做前缀索引,就是用列的前缀代替整个列作为索引key,当前缀长度合适时,可以做到既使得前缀索引的选择性接近全列索引,同时因为索引key变短而减少了索引文件的大小和维护开销。下面以employees.employees表为例介绍前缀索引的选择和使用。
从图12可以看到employees表只有一个索引
EXPLAIN SELECT * FROM employees.employees WHERE first_name='Eric' AND last_name='Anido'; +----+-------------+-----------+------+---------------+------+---------+------+--------+-------------+ | id | select_type | table | type | possible_keys | key | key_len | ref | rows | Extra | +----+-------------+-----------+------+---------------+------+---------+------+--------+-------------+ | 1 | SIMPLE | employees | ALL | NULL | NULL | NULL | NULL | 300024 | Using where | +----+-------------+-----------+------+---------------+------+---------+------+--------+-------------+
如果频繁按名字搜索员工,这样显然效率很低,因此我们可以考虑建索引。有两种选择,建
SELECT count(DISTINCT(first_name))/count(*) AS Selectivity FROM employees.employees; +-------------+ | Selectivity | +-------------+ | 0.0042 | +-------------+ SELECT count(DISTINCT(concat(first_name, last_name)))/count(*) AS Selectivity FROM employees.employees; +-------------+ | Selectivity | +-------------+ | 0.9313 | +-------------+
SELECT count(DISTINCT(concat(first_name, left(last_name, 3))))/count(*) AS Selectivity FROM employees.employees; +-------------+ | Selectivity | +-------------+ | 0.7879 | +-------------+
选择性还不错,但离0.9313还是有点距离,那么把last_name前缀加到4:
SELECT count(DISTINCT(concat(first_name, left(last_name, 4))))/count(*) AS Selectivity FROM employees.employees; +-------------+ | Selectivity | +-------------+ | 0.9007 | +-------------+
这时选择性已经很理想了,而这个索引的长度只有18,比
ALTER TABLE employees.employees ADD INDEX `first_name_last_name4` (first_name, last_name(4));
此时再执行一遍按名字查询,比较分析一下与建索引前的结果:
SHOW PROFILES; +----------+------------+---------------------------------------------------------------------------------+ | Query_ID | Duration | Query | +----------+------------+---------------------------------------------------------------------------------+ | 87 | 0.11941700 | SELECT * FROM employees.employees WHERE first_name='Eric' AND last_name='Anido' | | 90 | 0.00092400 | SELECT * FROM employees.employees WHERE first_name='Eric' AND last_name='Anido' | +----------+------------+---------------------------------------------------------------------------------+
性能的提升是显著的,查询速度提高了120多倍。
前缀索引兼顾索引大小和查询速度,但是其缺点是不能用于ORDER BY和GROUP BY操作,也不能用于Covering index(即当索引本身包含查询所需全部数据时,不再访问数据文件本身)。
InnoDB的主键选择与插入优化
在使用InnoDB存储引擎时,如果没有特别的需要,请永远使用一个与业务无关的自增字段作为主键。
经常看到有帖子或博客讨论主键选择问题,有人建议使用业务无关的自增主键,有人觉得没有必要,完全可以使用如学号或身份证号这种唯一字段作为主键。不论支持哪种论点,大多数论据都是业务层面的。如果从数据库索引优化角度看,使用InnoDB引擎而不使用自增主键绝对是一个糟糕的主意。
上文讨论过InnoDB的索引实现,InnoDB使用聚集索引,数据记录本身被存于主索引(一颗B+Tree)的叶子节点上。这就要求同一个叶子节点内(大小为一个内存页或磁盘页)的各条数据记录按主键顺序存放,因此每当有一条新的记录插入时,MySQL会根据其主键将其插入适当的节点和位置,如果页面达到装载因子(InnoDB默认为15/16),则开辟一个新的页(节点)。
如果表使用自增主键,那么每次插入新的记录,记录就会顺序添加到当前索引节点的后续位置,当一页写满,就会自动开辟一个新的页。如下图所示:
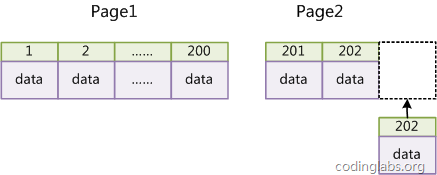
图13
这样就会形成一个紧凑的索引结构,近似顺序填满。由于每次插入时也不需要移动已有数据,因此效率很高,也不会增加很多开销在维护索引上。
如果使用非自增主键(如果身份证号或学号等),由于每次插入主键的值近似于随机,因此每次新纪录都要被插到现有索引页得中间某个位置:
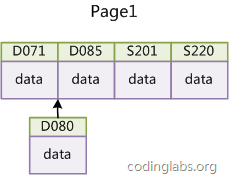
图14
此时MySQL不得不为了将新记录插到合适位置而移动数据,甚至目标页面可能已经被回写到磁盘上而从缓存中清掉,此时又要从磁盘上读回来,这增加了很多开销,同时频繁的移动、分页操作造成了大量的碎片,得到了不够紧凑的索引结构,后续不得不通过OPTIMIZE TABLE来重建表并优化填充页面。
因此,只要可以,请尽量在InnoDB上采用自增字段做主键。
后记
I have been writing this article intermittently for half a month, and the main content is the above. It is undeniable that this article is a bit of an armchair exercise to a certain extent, because my use of MySQL is at a novice level, and I don’t have much experience in database tuning. It would be a bit presumptuous to talk about database index tuning here. Just treat it as my personal study notes.
In fact, database index tuning is a technical activity that cannot just rely on theory, because the actual situation is ever-changing, and MySQL itself has very complex mechanisms, such as query optimization strategies and implementation differences of various engines, etc. The situation becomes more complicated. But at the same time, these theories are the basis of index tuning. Only by understanding the theory can we make reasonable inferences about the tuning strategy and understand the mechanism behind it. Then, combined with continuous experimentation and exploration in practice, we can truly achieve efficient use of MySQL. The purpose of indexing.
In addition, MySQL indexes and their optimization cover a very wide range, and this article only touches part of it. For example, topics related to index optimization and covering index (Covering index) related to sorting (ORDER BY) are not covered in this article. In addition to B-Tree indexes, MySQL also supports hash indexes, full-text indexes, etc. based on different engines. This article also does not cover Not covered. If you have the chance, I hope to add some parts that are not covered in this article.
References
[1] Baron Scbwartz et al., translated by Wang Xiaodong et al.; High Performance MySQL; Electronic Industry Press, 2010
[2] Written by Michael Kofler, translated by Yang Xiaoyun and others; The Definitive Guide to MySQL5; People's Posts and Telecommunications Publishing House, 2006
[3] Written by Jiang Chengyao; MySQL Technology Insider-InnoDB Storage Engine; Machinery Industry Press, 2011
[4] D Comer, Ubiquitous B-tree; ACM Computing Surveys (CSUR), 1979
[5] Codd, E. F. (1970). “A relational model of data for large shared data banks”. Communications of the ACM, , Vol. 13, No. 6, pp. 377-387
[6] MySQL5.1 Reference Manual – http://dev.mysql.com/doc /refman/5.1/zh/index.html
For more detailed explanations of the data structure and algorithm principles behind MySQL indexes, please pay attention to the PHP Chinese website!

