Detailed explanation of JavaScript tree structure

Everyone must be familiar with the data structure "tree". Today, we will review the binary tree and tree in the data structure and implement them with JavaScript.

ps: The tree structure is vividly reflected in many places in the front-end, such as Vue's virtual DOM and bubbling, etc.

Binary tree

--Concept--

Binary tree is a tree structure. Its characteristic is that each node has at most two subtrees (that is, there are no There are nodes with degree greater than 2), and the subtrees of the binary tree can be divided into left and right subtrees, and their order cannot be reversed arbitrarily.

The following is a binary tree (note: the following examples of binary trees are all based on this binary tree):

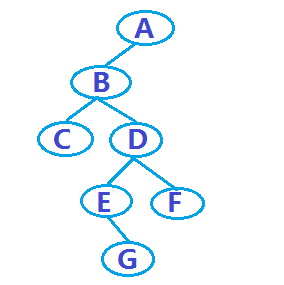
And, traversing the binary tree (traversing binary tree), there are three commonly used methods, as follows:

1), pre-order traversal of the binary tree (left and right of the root)

If the binary tree is empty, no operation; otherwise

-- Access root nodes;

-Elves the left sub -tree in the prelude;

For example, for the binary tree in the above example, the traversal result is as follows:

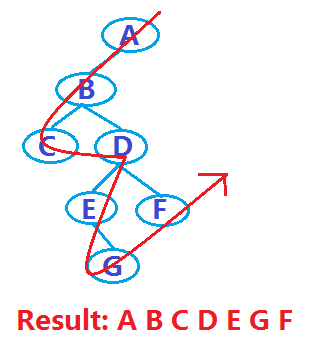2), in-order traversal of the binary tree (left root right)

                                                                                                               No operation; otherwise Right subtree.

For example, for the binary tree in the above example, the traversal result is as follows:

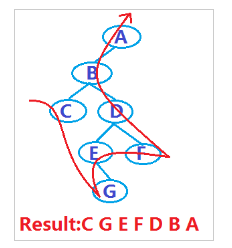
3), post-order traversal of the binary tree (left and right roots)

If the binary tree is empty, no operation; otherwise

 — Traverse the left subtree in post-order;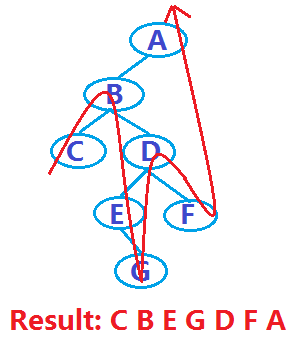

  —Traverse the right subtree in post-order;

--Visit the root Node.

For example, for the binary tree in the above example, the traversal result is as follows:

Okay, now that we understand the binary tree and the traversal method, let’s do it together Use JavaScript to implement it, of course using a chain storage structure.

First, use the JavaScript constructor to establish a binary tree node, as follows:

function TreeNode(){
 this.data = null;//该节点数据
 this.lchild = null;//左子树
 this.rchild = null;//右子树   
};

Then, we can construct a binary tree through the algorithm of traversing the binary tree, as follows, using Method to build a binary tree using pre-order sequence:

/*
*method:采用先序序列建立二叉树
*@params: nodeList（Array） --树节点，以先序序列存入数组中，null代表空节点
*/
TreeNode.createBiTree = function(nodeList){
 var i = 0;
 return (function getNode(){
  var node = null,
   val = nodeList[i++];
  if(!val){
   node = null;
  }else{
   node = new TreeNode();
   node.data = val;
   node.lchild = getNode();
   node.rchild = getNode();
  }
  return node;
 })();
};

Finally, it is to traverse a binary tree, which are pre-order traversal (PreOrderTraverse), in-order traversal (InOrderTraverse) and post-order traversal (PostOrderTraverse), as follows:

TreeNode.prototype = {
 constructor: TreeNode,
 _PreOrderTraverse: function(node){
  if(node){
   console.log(node.data);
   this._PreOrderTraverse(node.lchild);
   this._PreOrderTraverse(node.rchild);
  }
 },
 PreOrderTraverse: function(){
  console.log('PreOrder:');
  this._PreOrderTraverse(this);
 },
 _InOrderTraverse: function(node){
  if(node){
   this._InOrderTraverse(node.lchild);
   console.log(node.data);
   this._InOrderTraverse(node.rchild);
  }
 },
 InOrderTraverse: function(){
  console.log('InOrder:');
  this._InOrderTraverse(this);
 },
 _PostOrderTraverse: function(node){
  if(node){
   this._PostOrderTraverse(node.lchild);
   this._PostOrderTraverse(node.rchild);
   console.log(node.data);
  }
 },
 PostOrderTraverse: function(){
  console.log('PostOrder:');
  this._PostOrderTraverse(this);
 }
};

Okay, using the above binary tree example, we can test it ourselves:

var treeNode = null,
 nodeList = ['A', 'B', 'C', null, null, 'D', 'E', null, 'G', null, null, 'F', null, null, null];
//getting a binary tree from nodeList
treeNode = TreeNode.createBiTree(nodeList);
//traversing the tree of treeNode
treeNode.PreOrderTraverse();//ABCDEGF
treeNode.InOrderTraverse();//CBEGDFA
treeNode.PostOrderTraverse();//CGEFDBA

Tree

--Concept--

A tree is a finite set of n (n>=0) nodes. In any non-empty tree, there is and is only one specific node called the root. When n>1, the remaining nodes can be divided into m (m>0) mutually disjoint finite nodes. Sets, each of which is itself a tree, called a subtree of the root. Of course, binary trees definitely belong to trees.

The following is a tree (note: the tree-related examples below are all based on this tree):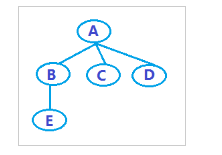

And, traverse more than one tree There are two commonly used traversal methods for child trees, as follows:

1) Root-first traversal, which is similar to depth-first search (Depth_First Search) traversal. They all use the stack to traverse elements, as follows:

2), traversal by level, similar to Breadth_First Search traversal. They all use queues to traverse elements, as follows:

Okay, now that we understand the tree and the traversal method, let’s use JavaScript to implement it together. Of course It also uses a chain storage structure.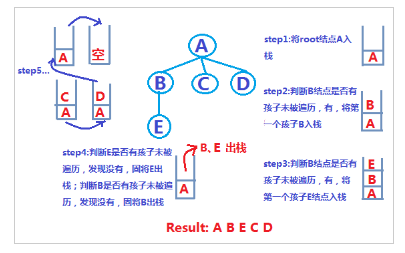

First, use JavaScript to create tree nodes, as follows:

/*
*@Params: data --节点数据
   children -- 所有孩子结点
*/
function TreeNode(data, children){
 if(!(this instanceof TreeNode)){
  return new TreeNode(data, children);
 }
 this.data = data || null;
 this.children = children || [];
};

根据上述TreeNode构造函数，我们可以将例子中的树，表示如下：

var treeNode = TreeNode('A', [
       TreeNode('B', [TreeNode('E')]),
       TreeNode('C'),
       TreeNode('D')
     ]);

接着，就是编写遍历树方法咯，分别为先根遍历和按层次遍历，如下：

TreeNode.prototype = {
 constructor: TreeNode,
 _traverseAsDFS: function(node){//先根遍历
  var self = this;
  if(node){
   console.log(node.data);
   node.children.forEach(function(child){
    if(child.children.length){
     self._traverseAsDFS(child);
    }else{
     console.log(child.data);
    }
   });
  }
 },
 traverseAsDFS: function(){
  console.log('Depth_First Search');
  this._traverseAsDFS(this);
 },
 traverseAsBFS: function(){//按层次遍历
  var queue = [];
  console.log('Breadth_First Search');
  console.log(this.data);
  if(this.children.length){
   queue.push(this);
  }
  while(queue.length){
   let tempNode = queue.shift();
   tempNode.children.forEach(function(child){
    console.log(child.data);
    if(child.children.length){
     queue.push(child);
    }      
   });
  }
 }
};

   

好了，利用上述二叉树例子，我们可以自行测试下：

var treeNode = TreeNode('A', [
       TreeNode('B', [TreeNode('E')]),
       TreeNode('C'),
       TreeNode('D')
     ]);
treeNode.traverseAsDFS();//ABECD
treeNode.traverseAsBFS();//ABCDE

关于上述全部代码，见github。

以上就是本文的全部内容，希望本文的内容对大家的学习或者工作能带来一定的帮助，同时也希望多多支持脚本之家PHP中文网

更多Detailed explanation of JavaScript tree structure相关文章请关注PHP中文网！