Compilation of A* game path algorithm implemented by js ajax

Reposting some introductions [reprinted from http://data.gameres.com/message.asp?TopicID=25439]

I have known about the A* algorithm a long time ago, but have never read the relevant articles seriously. , I haven’t read the code, I just have a vague concept in my mind. This time I decided to start from scratch and study this highly recommended simple method as the beginning of learning artificial intelligence.
This article is very well-known. Many people in China should have translated it. I didn’t look it up. I think the translation itself is also an exercise for my English proficiency. After hard work, I finally completed the document and understood the principles of the A* algorithm. There is no doubt that the author uses vivid descriptions and concise and humorous language to describe this magical algorithm from simple to profound. I believe everyone who reads it will have some understanding of it (if not, then my translation is too poor. out--b).
Original link: http://www.gamedev.net/reference/articles/article2003.asp

The following is the translated text. (Since I use ultraedit to edit, I have not processed the various links in the original text (except for charts). This is also to avoid the suspicion of unauthorized links. Interested readers can refer to the original text.

Members not Difficult, the A* (pronounced A star) algorithm is indeed difficult for beginners

This article does not attempt to make an authoritative statement on this topic. Instead, it only describes the principles of the algorithm. , so that you can understand other related information in further reading.

Finally, this article has no program details. You can implement it in any computer programming language as you wish. The end contains a link to the example program. The compressed package includes C and Blitz Basic language versions. If you just want to see how it works, the executable file is also included. I'm improving myself. Let's start from the beginning. .

Sequence: Search area

Suppose someone wants to move from point A to point B, as shown below, the green one is the starting point A, and the red one is. is the end point B, and the blue square is the middle wall.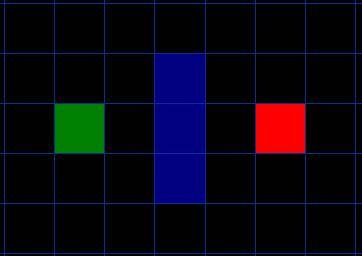




The first thing you notice is that the search area is divided into a square grid, like this. The search area is the first step in pathfinding. This method simplifies the search area into a two-dimensional array. Each element of the array is a square in the grid, and the squares are marked as passable and impassable paths. Described as the collection of squares we pass from A to B. Once the path is found, our person walks from the center of one square to another until reaching the destination. These midpoints are called. "Nodes". When you read other pathfinding materials, you will often see people talking about nodes. Why not describe them as squares? Because it is possible that your path is divided into other structures that are not squares. They can be rectangular, hexagonal, or any other shape. Nodes can be placed anywhere in the shape - in the center, or along the borders, or whatever. We use this system as it is. The simplest.

Start the search

Just like we did with the grid above, once the search area is transformed into tractable nodes, the next step is to guide a search to find the shortest path. . In the A* pathfinding algorithm, we start from point A, check adjacent squares, and expand outward until we find the target. We do the following to start the search:

.
1. Start from point A and save it as a pending point. The open list is like a shopping list. Although there is only one element in the list now, there will be more in the future. The path may pass through the squares it contains, or it may not. Basically, this is a list of squares to be checked.
2. Find all reachable or passable squares around the starting point, skipping any. Walls, water, or other blocks of impassable terrain. Also add them to the open list. Save point A as the "parent square" for all these squares. When we want to describe a path, the information of the parent square is very important. Its specific use will be explained later.
3. Delete point A from the open list and add it to a "closed list", which stores all squares that do not need to be checked again.

At this point, you should have a structure like the one pictured. In the picture, the dark green square is the center of your starting square. It is outlined in light blue to indicate that it has been added to the close list. All adjacent cells are now in the open list, and they are outlined in light green. Each square has a gray pointer pointing back to their parent square, which is the starting square.





Next, we choose to open the adjacent square in the list and roughly repeat the previous process, as follows. But which square should we choose? It's the one with the lowest F value.

Path Score
The key to choosing which square to pass through in the path is the following equation:

F = G H

Here:
* G = The cost of moving from the starting point A to the specified square on the grid along the generated path.
* H = The estimated movement cost of moving from that square on the grid to end point B. This is often called a heuristic, which can be a little confusing to you. The reason it's called that is because it's just a guess. We have no way of knowing the length of the path in advance because there may be various obstacles on the way (walls, water, etc.). Although this article only provides one method for calculating H, you can find many other methods online.

Our path is generated by iteratively traversing the open list and selecting the square with the lowest F value. The article will describe this process in more detail. First, let's take a closer look at how to calculate this equation.

As mentioned above, G represents the cost of moving along the path from the starting point to the current point. In this example, we set the cost of horizontal or vertical movement to be 10 and the diagonal cost to be 14. We take these values ​​because the distance along the diagonal is square root of 2 (don't be afraid), or about 1.414 times the cost of moving horizontally or vertically. For simplicity, we use 10 and 14 as approximations. The proportions are mostly correct, and we avoid root operations and decimals. It's not just because we're afraid of trouble or don't like math. Using integers like this is also faster for the computer. You'll soon find that if you don't use these simplifications, pathfinding will be very slow.

Since we are calculating the G value leading to a certain square along a specific path, the method of evaluation is to take the G value of its parent node, and then determine whether it is diagonal or right-angled relative to the parent node. (off-diagonal), increase by 14 and 10 respectively. This method becomes more demanding in the example because we are getting more than one square from the starting square.

H value can be estimated using different methods. The method we use here is called the Manhattan method, which calculates the sum of the number of horizontal and vertical squares from the current square to the destination square, ignoring the diagonal direction. Then multiply the result by 10. This is called the Manhattan method because it looks like counting the number of blocks from one place to another in a city where you can't go diagonally across blocks. It is very important that we ignore all obstacles. This is an estimate of the remaining distance, not an actual value, which is why this method is called a heuristic. Want to know more? You can find the equations and additional notes here.

The value of F is the sum of G and H. The results of the first step of the search can be seen in the chart below. Grades of F, G and H are written in each box. As indicated by the squares immediately to the right of the starting square, F is printed in the upper left corner, G in the lower left corner, and H in the lower right corner.



Now let’s take a look at the squares. In the letter square, G = 10. This is because it is only one space away from the starting cell in the horizontal direction. The G values ​​of the squares immediately above, below and to the left of the starting square are all equal to 10. The G value in the diagonal direction is 14.

The H value is obtained by solving the Manhattan distance to the red target grid, which only moves in the horizontal and vertical directions, and ignores the middle wall. Using this method, the square immediately to the right of the starting point is 3 squares away from the red square, and the H value is 30. The square above this square is 4 squares away (remember, it can only be moved horizontally and vertically) and has an H value of 40. You should roughly know how to calculate the H value of other squares~.

The F value of each grid is still simply the sum of G and H.

Continue the search

In order to continue the search, we simply select F from the open list The square with the lowest value. Then, do the following processing for the selected square:

4. Delete it from the open list, and then add it to the closed list.
5. Check all adjacent grids. Skip those that are already on the closed list or are impassable (terrain with walls, water, or other impassable terrain) and add them to the open list if they are not already there. Make the selected square the parent node of the new square.
6. If an adjacent grid is already in the open list, check whether the current path is better. In other words, check if the G value would be lower if we reached it using a new path. If not, then do nothing.
On the other hand, if the new G value is lower, then change the parent node of the adjacent square to the currently selected square (in the diagram above, change the direction of the arrow to point to this square) . Finally, recalculate the values ​​of F and G. If this doesn't seem clear enough, you can look at the diagram below.

Okay, let’s see how it works. Of our original 9-square grid, after the starting point was switched to the closed list, there were 8 left in the open list. Among them, the one with the lowest F value is the grid immediately to the right of the starting grid, and its F value is 40. Therefore we select this square as the next square to be processed. In the following figure, it is highlighted in blue.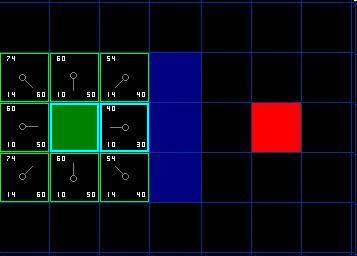




First, we take it out of the open list and put it into the closed list (that's why it's highlighted in blue). Then we check adjacent cells. Oh, the grid on the right is a wall, so we skip it. The grid on the left is the starting grid. It's in the close list, so we skip it as well.

The other 4 squares are already in the open list, so we check the G value to determine whether the path is better if we get there through this square. Let's look at the squares below the selected grid. Its G value is 14. If we move there from the current square, the G value will be equal to 20 (the G value of reaching the current square is 10, and moving to the upper square will increase the G value by 10). Because the G value of 20 is greater than 14, this is not a better path. If you look at the picture, you can understand. Instead of moving one square horizontally and then one vertically, it would be easier to just move one square diagonally.

When we repeat this process for the 4 neighboring cells that are already in the open list, we find that none of the paths can be improved by using the current cell, so we don't make any changes. Now that we have checked all adjacent cells, we can move to the next cell.

So we search the open list. Now there are only 7 cells in it. We still choose the one with the lowest F value. What's interesting is that this time, two grids have a value of 54. How do we choose? It's not troublesome. In terms of speed, it is faster to select the last grid added to the list. This leads to the preference to use newly found grids first when approaching the goal during the pathfinding process. But it doesn't matter. (Different treatments of the same values ​​lead to different versions of the A* algorithm finding different paths of equal length.)

Then we select the grid at the bottom right of the starting grid, as shown in the figure.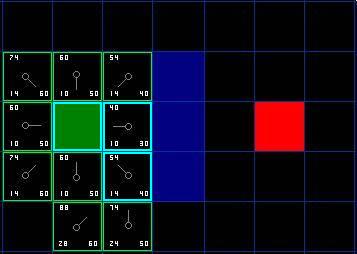




This time, when we checked the adjacent grid, we found that there was a wall on the right side, so we skipped it. The top box is also skipped. We also skipped the grid below the wall. Why? Because you can't reach that square directly without going through the corner. You really need to go down first and then reach that block, and walk through that corner step by step. (Note: The rule for crossing corners is optional. It depends on how your nodes are placed.)

That leaves the other 5 squares. The other two cells below the current cell are not currently in the open list, so we add them and specify the current cell as their parent node. Of the remaining 3 squares, two are already in the open list (the starting square, and the square above the current square, are highlighted in blue in the table), so we skip them. The last square, to the left of the current square, will be checked to see if the G value is lower through this path. Don't worry, we're ready to check the next box in the open list.

We repeat this process until the target cell is added to the open list, as seen in the image below.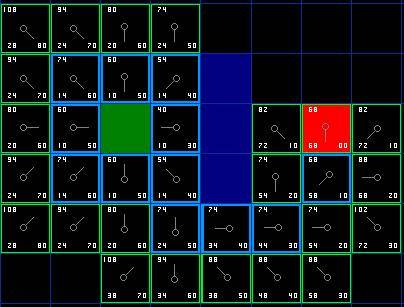




Note that the parent node of the grid below the starting grid is different from the previous one. Previously its G value was 28 and pointed to the upper right grid. Its G value is now 20, pointing to the square above it. This happens somewhere in the pathfinding process, when the new path is applied, the G value is checked and becomes lower - so the parent node is reassigned and the G and F values ​​are recalculated. Although this change is not important in this example, on many occasions this change can cause drastic changes in pathfinding results.

So, how do we determine this path? It's very simple, start from the red target grid and move towards the parent node in the direction of the arrow. This will eventually lead you back to the starting square, and that's your path! It should look like the picture. Moving from starting grid A to target grid B is simply a matter of moving along the path from the midpoint of each grid (node) to the next until you reach the target point. It's that simple.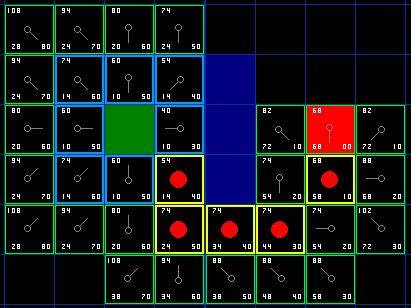





A* method summary

Okay, now that you have read the entire description, let us write down each step of the operation in Together:

1. Add the starting grid to the open list.
2. Repeat the following work:
a) Find the grid with the lowest F value in the open list. We call it the current grid.
b) Switch it to close the list.
c) For each of the 8 adjacent cells?
* If it is not passable or is already on the closed list, skip it. The opposite is as follows.
* If it is not in the open list, add it to it. Make the current grid the parent node of this grid. Record the F, G, and H values ​​of this grid.
* If it is already in the open list, use the G value as a reference to check whether the new path is better. Lower G means a better path. If so, change the parent node of this cell to the current cell, and recalculate the G and F values ​​of this cell. If you keep your open list sorted by F value, you may need to reorder the open list after changing it.

D) Stop, when you *add the target grid into the opening list. At this time, the path is found, or
*No target grid is found, and the list is empty. At this time, the path does not exist.
3. Save path. Starting from the target cell, move along the parent node of each cell until you return to the starting cell. This is your path.

Digression

I’m off topic, sorry, but it’s worth mentioning that when you see different discussions about A* on the Internet or in related forums, you sometimes see some that are regarded as code for the A* algorithm when in fact they are not. To use A*, you must include all the elements discussed above - specific open and close lists, and use F, G and H for path evaluation. There are many other pathfinding algorithms, but they are not A*, which is considered the best of them all. Bryan Stout discusses some of them, including some of their advantages and disadvantages, in the reference documentation later in this article. Sometimes other algorithms are better in certain situations, but you have to know exactly what you are doing. Okay, enough of that. Back to the article.

Implementation Notes

Now that you understand the basic principles, there are a few additional things to consider when writing your program. Some of the material below refers to programs I wrote in C and Blitz Basic, but code written in other languages ​​is equally valid.

1. Maintain the open list: This is the most important component of the A* pathfinding algorithm. Every time you access the open list, you need to look for the square with the lowest F value. There are a few different ways to accomplish this. You can save the path elements at will, and when you need to find the element with the lowest F value, traverse the open list. This is simple, but too slow, especially for long paths. This can be improved by maintaining a sorted list of cells. Each time you find the cell with the lowest F value, you only need to select the first element of the list. This approach is my first choice when implementing it myself.

On the mini map. This method works well, but it's not the fastest solution. A* programmers who are more demanding about speed use a method called "binary heap", which is also the method I use in my code. Based on my experience, this method will be 2 to 3 times faster in most situations, and the speed will increase exponentially (more than 10 times faster) on long paths. If you want to learn more about binary heaps, check out my article, Using Binary Heaps in A* Pathfinding.

2. Other units: If you happen to look at my example code, you will find that it completely ignores other units. My wayfinders can actually travel through each other. Depending on the specific game, this may or may not work. If you are going to consider other units in the hope that they can bypass each other, I recommend ignoring other units in the pathfinding algorithm and writing some new code for collision detection. When a collision occurs, you can generate a new path or use some standard movement rules (e.g. always right, etc.) until there are no obstacles in the way, and then generate a new path. Why aren't other units considered in the initial path calculation? That's because other units will move, and by the time you get to their original location, they may have left. This can lead to strange results, with a unit swerving to avoid a unit that is no longer there, and bumping into units that rush into its path after calculating the path.

However, ignoring other objects in the pathfinding algorithm means you have to write separate collision detection code. This varies from game to game, so I leave that decision up to you. In the reference list, Bryan Stout's article is worth looking into as it has some possible solutions (like robust tracking, etc.).

3. Some speed tips: When you develop your own A* program, or rewrite mine, you will find that pathfinding takes up a lot of CPU time, especially on large maps with a lot of objects. When finding your way. If you read other materials on the Internet, you will understand that even the experts who developed StarCraft or Age of Empires can't help it. If you feel that pathfinding is too slow, here are some suggestions that may help:

* Use a smaller map or fewer pathfinders.
* Don’t find paths for multiple objects at the same time. Instead, add them to a queue and spread the pathfinding process over several game cycles. If your game runs at 40 cycles per second, no one will notice. But they'll find the game suddenly slows down when a large number of pathfinders calculate their paths.
* Try to use a larger map grid. This reduces the total number of grids searched in pathfinding. If you're ambitious, you can design two or more pathfinding systems to be used in different situations, depending on the length of the path. This is exactly what pros do, use large areas to calculate long paths, and then switch to fine-grained pathfinding using small grids/areas as they get closer to the target. If you are interested in this idea, check out my article Two-Tiered A* Pathfinding.
* Use the waypoint system to calculate long paths, or pre-calculate paths and add them to the game.
* Preprocess your map to indicate which areas of the map are inaccessible. I call these areas "islands." In fact, they can be islands or other inaccessible areas surrounded by walls. The lower bound of A* is that when you tell it to find a path to those areas, it will search the entire map until all reachable squares/nodes have been calculated by opening and closing the list. This wastes a lot of CPU time. This can be avoided by predetermining these areas (e.g. via flood-fill or similar), recording this information in some kind of array, and checking it before starting pathfinding. In my Blitz version of the code, I built a map preprocessor to do this job. It also marks dead ends that the pathfinding algorithm can ignore, which further increases pathfinding speed.

4. Different terrain losses: In this tutorial and the program I attached, there are only two types of terrain - passable and impassable. But you may need some terrain that is traversable but more expensive to move around - swamps, hills, dungeon stairs, etc. These are traversable terrain but more expensive to move than flat open areas. Similarly, roads should be less expensive to move than natural terrain.

This problem is easily solved by adding terrain loss when calculating the G value of any terrain. Simply add some extra loss to it. Since the A* algorithm has been designed to find the path with the lowest cost, it can easily handle this situation. In the simple example I provided, there are only two types of terrain: passable and impassable. A* will find the shortest and most direct path. But where terrain costs vary, the least expensive path may involve a long distance of travel—like following a path around a swamp rather than directly through it.

One situation that requires additional consideration is what experts call "influence mapping" (tentative translation: influence mapping). Just like the different terrain costs described above, you can create an additional point system and apply it to the pathfinding AI. Suppose you have a map with a large number of pathfinders, all of whom are passing through a mountainous area. Every time the computer generates a path through that pass, it becomes more crowded. If you wish, you can create an influence map that adversely affects hexes with a large number of carnage events. This will make the computer prefer safer paths, and help it avoid constantly sending parties and pathfinders to a particular path simply because it's shorter (but potentially more dangerous).

5. Dealing with Unknown Areas: Have you ever played a PC game where the computer always knows which path is correct, even if it hasn't scouted the map yet? For games, too good a pathfinding can seem unrealistic. Fortunately, this is a problem that can be easily solved.

The answer is to create a separate "knownWalkability" array for each different player and computer (per player, not per unit - that would consume a lot of memory), each containing the player Areas that have been explored, and other areas that are considered passable until proven otherwise. With this approach, units will linger at the dead end of the road and make poor choices until they find their way around. Once the map is explored, pathfinding proceeds as usual.

6. Smooth path: Although A* provides the shortest, lowest-cost path, it cannot automatically provide a smooth-looking path. Take a look at the resulting path for our example (in Figure 7). The first step is to the lower right of the starting grid. If this step was directly downward, wouldn't the path be smoother?

There are several ways to solve this problem. It is possible to adversely affect the direction of the grid when calculating the path, adding an additional value to the G value. Alternatively, you can run along the path after it is calculated and look for places where replacing adjacent squares will make the path look smoother. For complete results, check out Toward More Realistic Pathfinding, a (free, but registration required) article by Marco Pinter on Gamasutra.com

7. Non-square search area: In our case, we Use a simple 2D square plot. You don't have to use this method. You can use irregularly shaped areas. Think of the game of Adventure Chess, and the countries in it. You could design a pathfinding level like that. To do this, you may need to create a table of country adjacencies, and the G values ​​for moving from one country to another. You also need a way to estimate the H value. Everything else is exactly the same as in the example. When you need to add a new element to the open list, you don't need to use adjacent cells. Instead, look for adjacent countries from the table.

Similarly, you can create a system of waypoints for a defined terrain map. Waypoints are typically turning points on roads or dungeon passages. As a game designer, you can preset these waypoints. Two waypoints are considered adjacent if there are no obstacles in the straight line between them. In the Adventure Chess example, you can save this adjacent information in a table and use it when you need to add elements to the open list. Then you can record the associated G value (possibly using the straight-line distance between two points), H value (possibly using the straight-line distance to the target point), and just do the rest as before.

For another example of searching an RPG map in a non-square area, check out my article Two-Tiered A* Pathfinding.

Further Reading

Okay, now you have a preliminary understanding of some further points. At this point, I recommend you study my source code. The package contains two versions, one written in C and the other in Blitz Basic. By the way, both versions are well annotated and easy to read, here are the links.

* Example code: A* Pathfinder (2D) Version 1.71

If you are using neither C nor Blitz Basic, there are two small executable files in the C version. Blitz Basic can be run on the demo version of Blitz Basic 3D (not Blitz Plus), which can be downloaded for free from the Blitz Basic website. An online demo provided by Ben O'Neill can be found here.

You should also take a look at the following web pages. After reading this tutorial, they should become much easier to understand.

* Amit’s A* page: This is a widely cited page produced by Amit Patel, which may be a bit difficult to understand if you haven’t read this article beforehand. Worth a look. Especially Amit's own views on this issue.
* Smart Moves: Intelligent pathfinding: This article published by Bryan Stout on Gamasutra.com requires registration to read. Registration is free and well worth the price compared to this article and other resources on the site. The programs Bryan wrote in Delphi helped me learn A* and were the source of inspiration for my A* code. It also describes several variations of A*.
* Terrain Analysis: This is an advanced, but fun topic, written by Dave Pottinge, an expert at Ensemble Studios. This guy was involved in the development of Age of Empires and Age of Kings. Don't expect to understand everything here, but it's an interesting article that might give you some ideas of your own. It contains some insights into mip-mapping, influence mapping, and other advanced AI/pathfinding perspectives. The discussion of "flood filling" gave me the inspiration for my own "dead ends" and "islands" of code, which are included in my Blitz version of the code.

Some other sites worth checking out:

* aiGuru: Pathfinding
* Game AI Resource: Pathfinding
* GameDev.net: Pathfinding

Okay , that's all. If you happen to write a program that uses these ideas, I'd like to hear about it. You can contact me like this:
Now, good luck!

I found hjjboy’s friend’s js implementation method on 51js. I added comments to facilitate encapsulation in the future.

The code is as follows:

<html><head><title>use A* to find path...</title></head> 
<body style="margin:0px"> 
<script> 
/* 
written by hjjboy 
email:tianmashuangyi@163.com 
qq:156809986 
*/ 
var closelist=new Array(),openlist=new Array();//closelist保存最终结果。openlist保存临时生成的点； 
var gw=10,gh=10,gwh=14;//参数 gh是水平附加参数 gwh是四角的附加参数。 
var p_start=new Array(2),p_end=new Array(2);//p_start为起点，p_end为终点 
var s_path,n_path="";//s_path为当前点 n_path为障碍物数组样式的字符串. 
var num,bg,flag=0; 
var w=30,h=20; 
function GetRound(pos){//返回原点周围的8个点 
    var a=new Array(); 
    a[0]=(pos[0]+1)+","+(pos[1]-1); 
    a[1]=(pos[0]+1)+","+pos[1]; 
    a[2]=(pos[0]+1)+","+(pos[1]+1); 
    a[3]=pos[0]+","+(pos[1]+1); 
    a[4]=(pos[0]-1)+","+(pos[1]+1); 
    a[5]=(pos[0]-1)+","+pos[1]; 
    a[6]=(pos[0]-1)+","+(pos[1]-1); 
    a[7]=pos[0]+","+(pos[1]-1); 
    return a; 
} 
function GetF(arr){ //参数为原点周围的8个点 
    var t,G,H,F;//F,综合的距离值，H,距离值 G,水平\角落附加计算 
    for(var i=0;i<arr.length;i++){ 
        t=arr[i].split(","); 
        t[0]=parseInt(t[0]); 
        t[1]=parseInt(t[1]); 
        if(IsOutScreen([t[0],t[1]])||IsPass(arr[i])||InClose([t[0],t[1]])||IsStart([t[0],t[1]])||!IsInTurn([t[0],t[1]])) 
            continue;//如果上面条件有一满足，则跳过本次循环，进行下一次。 
        if((t[0]-s_path[3][0])*(t[1]-s_path[3][1])!=0)//判断该点是否处于起点的垂直或横向位置上 
            G=s_path[1]+gwh;//如果不在G=14; 
        else 
            G=s_path[1]+gw;//如果在G=10; 
        if(InOpen([t[0],t[1]])){//如果当前点已存在openlist数组中 
            if(G<openlist[num][1]){ 
            maptt.rows[openlist[num][4][1]].cells[openlist[num][4][0]].style.backgroundColor="blue";//调试 
                openlist[num][0]=(G+openlist[num][2]); 
                openlist[num][1]=G; 
                openlist[num][4]=s_path[3]; 
            } 
            else{G=openlist[num][1];} 
        } 
        else{ 
            H=(Math.abs(p_end[0]-t[0])+Math.abs(p_end[1]-t[1]))*gw; 
            F=G+H; 
            arr[i]=new Array(); 
            arr[i][0]=F; 
            arr[i][1]=G; 
            arr[i][2]=H; 
            arr[i][3]=[t[0],t[1]]; 
            arr[i][4]=s_path[3]; 
            openlist[openlist.length]=arr[i];//将F等信息保存到openlist 
        } 
        if(maptt.rows[t[1]].cells[t[0]].style.backgroundColor!="#cccccc"&&maptt.rows[t[1]].cells[t[0]].style.backgroundColor!="#0000ff"&&maptt.rows[t[1]].cells[t[0]].style.backgroundColor!="#ff0000"&&maptt.rows[t[1]].cells[t[0]].style.backgroundColor!="#00ff00") 
        { 
            maptt.rows[t[1]].cells[t[0]].style.backgroundColor="#FF00FF"; 
            if(F!=undefined) 
            maptt.rows[t[1]].cells[t[0]].innerHTML="<font color=&#39;black&#39;>"+F+"</font>"; 
        } 
    } 
} 
function IsStart(arr){ //判断该点是不是起点 
    if(arr[0]==p_start[0]&&arr[1]==p_start[1]) 
        return true; 
    return false; 
} 
function IsInTurn(arr){ //判断是否是拐角 
    if(arr[0]>s_path[3][0]){ 
        if(arr[1]>s_path[3][1]){ 
            if(IsPass((arr[0]-1)+","+arr[1])||IsPass(arr[0]+","+(arr[1]-1))) 
                return false; 
        } 
        else if(arr[1]<s_path[3][1]){ 
            if(IsPass((arr[0]-1)+","+arr[1])||IsPass(arr[0]+","+(arr[1]+1))) 
                return false; 
        } 
    } 
    else if(arr[0]<s_path[3][0]){ 
        if(arr[1]>s_path[3][1]){ 
            if(IsPass((arr[0]+1)+","+arr[1])||IsPass(arr[0]+","+(arr[1]-1))) 
                return false; 
        } 
        else if(arr[1]<s_path[3][1]){ 
            if(IsPass((arr[0]+1)+","+arr[1])||IsPass(arr[0]+","+(arr[1]+1))) 
                return false; 
        } 
    } 
    return true; 
} 
function IsOutScreen(arr){ //是否超出场景范围 
    if(arr[0]<0||arr[1]<0||arr[0]>(w-1)||arr[1]>(h-1)) 
        return true; 
    return false; 
} 
function InOpen(arr){//获得传入在openlist数组的位置，如不存在返回false，存在为true，位置索引保存全局变量num中。 
    var bool=false; 
    for(var i=0;i<openlist.length;i++){ 
        if(arr[0]==openlist[i][3][0]&&arr[1]==openlist[i][3][1]){ 
            bool=true;num=i;break;} 
    } 
    return bool; 
} 
function InClose(arr){ 
    var bool=false; 
    for(var i=0;i<closelist.length;i++){ 
        if((arr[0]==closelist[i][3][0])&&(arr[1]==closelist[i][3][1])){ 
            bool=true;break;} 
    } 
    return bool; 
} 
function IsPass(pos){ //pos这个点是否和障碍点重合  
    if((";"+n_path+";").indexOf(";"+pos+";")!=-1) 
        return true; 
    return false; 
} 
function Sort(arr){//整理数组，找出最小的F，放在最后的位置。 
    var temp; 
    for(var i=0;i<arr.length;i++){ 
        if(arr.length==1)break; 
        if(arr[i][0]<=arr[i+1][0]){ 
            temp=arr[i]; 
            arr[i]=arr[i+1]; 
            arr[i+1]=temp; 
        } 
        if((i+1)==(arr.length-1)) 
            break; 
    } 
} 
function main(){//主函数 
        alert(&#39;&#39;); 
        GetF(//把原点周围8点传入GetF进行处理。算A*核心函数了 :)，进行求F，更新openlist数组 
            GetRound(s_path[3]) //求原点周围8点 
        ); 
    debugp.innerHTML+="A："+openlist.join(&#39;|&#39;)+"<br />";//调试 
        Sort(openlist);//整理数组，找出最小的F，放在最后的位置。 
    debugp.innerHTML+="B："+openlist.join(&#39;|&#39;)+"<br />";//调试 
        s_path=openlist[openlist.length-1];//设置当前原点为F最小的点 
        closelist[closelist.length]=s_path;//讲当前原点增加进closelist数组中 
        openlist[openlist.length-1]=null;//从openlist中清除F最小的点 
    debugp.innerHTML+="C："+openlist.join(&#39;|&#39;)+"<br />";//调试 
        if(openlist.length==0){alert("Can&#39;t Find the way");return;}//如果openlist数组中没有数据了，则找不到路径 
        openlist.length=openlist.length-1;//上次删除把数据删了，位置还保留了，这里删除 
        if((s_path[3][0]==p_end[0])&&(s_path[3][1]==p_end[1])){//如果到到终点了，描绘路径 
            getPath(); 
        } 
        else{//否则循环执行,标准原点 
            maptt.rows[s_path[3][1]].cells[s_path[3][0]].style.backgroundColor="green";setTimeout("main()",100); 
        } 
} 
function getPath(){//描绘路径 
    var str=""; 
    var t=closelist[closelist.length-1][4]; 
    while(1){ 
        str+=t.join(",")+";"; 
        maptt.rows[t[1]].cells[t[0]].style.backgroundColor="#ffff00"; 
        for(var i=0;i<closelist.length;i++){ 
            if(closelist[i][3][0]==t[0]&&closelist[i][3][1]==t[1]) 
                t=closelist[i][4]; 
        } 
        if(t[0]==p_start[0]&&t[1]==p_start[1]) 
            break; 
    } 
    alert(str); 
} 
function setPos(){//初始原点为起点 
    var h=(Math.abs(p_end[0]-p_start[0])+Math.abs(p_end[1]-p_start[1]))*gw; 
    s_path=[h,0,h,p_start,p_start]; 
} 
function set(id,arr){//设置点的类型 
    switch(id){ 
        case 1: 
            p_start=arr; 
            maptt.rows[arr[1]].cells[arr[0]].style.backgroundColor="#ff0000";break; 
        case 2: 
            p_end=arr;maptt.rows[arr[1]].cells[arr[0]].style.backgroundColor="#0000ff";break; 
        case 3: 
            n_path+=arr.join(",")+";";maptt.rows[arr[1]].cells[arr[0]].style.backgroundColor="#cccccc";break; 
        default: 
            break; 
    } 
} 
function setflag(id){flag=id;} 
</script> 
<table id="maptt" cellspacing="1" cellpadding="0" border="0" bgcolor="#000000"> 
<script> 
for(var i=0;i<h;i++){ 
    document.write("<tr>"); 
    for(var j=0;j<w;j++){ 
        document.write(&#39;<td onclick="set(flag,[&#39;+j+&#39;,&#39;+i+&#39;]);" bgcolor="#ffffff" width="20" height="20"></td>&#39;); 
    } 
    document.write("</tr>"); 
} 
</script> 
</table> 
<a href="javascript:setflag(1);">StarPoint</a><br> 
<a href=&#39;javascript:setflag(2);&#39;>EndPoint</a><br> 
<a href=&#39;javascript:setflag(3);&#39;>Wall</a><br> 
<input type="button" onclick="setPos();main();this.disabled=true;" value="find"> 
<p id="debugp"></p> 
</body> 
</html>