How to parse computer code, Advent of Code ay 3

Having tackled some of the later Advent of Code challenges, I wanted to revisit Day 3, which presented an interesting parsing problem. The task involved extracting valid code from a noisy input, a great exercise in parser and lexer development. Join me as I explore my approach to this challenge.

A generated image showing my love for the puzzle (?) by Microsoft Copilot

When I first wrote about the ruler DSL, I relied on Hy for parsing. However, my recent exploration of generative AI has introduced a new parsing method: generated code using the funcparserlib library. This Advent of Code challenge allowed me to delve into the intricacies of funcparserlib and develop a much stronger grasp of the generated code's functionality.

Implementing the Lexer (Lexical Analysis)

The first step in processing our corrupted input is lexing (or tokenization). The lexer (or tokenizer) scans the input string and divides it into individual tokens, which are the basic building blocks for further processing. A token represents a meaningful unit in the input, categorized by its type. For this puzzle, we’re interested in these token types:

• Operators (OP): These represent function names, such as mul, do, and don't. For example, the input mul(2, 3) contains the operator token mul.
• Numbers: These are numerical values. For instance, in the input mul(2, 3), 2 and 3 would be recognized as number tokens.
• Commas: The comma character (,) acts as a separator between arguments.
• Parentheses: Opening ( and closing ) parentheses define the structure of the function calls.
• Gibberish: This category encompasses any characters or sequences of characters that don’t match the other token types. This is where the “corrupted” part of the input comes in. For example, %$#@ or any random letters would be considered gibberish.

While funcparserlib often uses magic strings in its tutorials, I prefer a more structured approach. Magic strings can lead to typos and make it difficult to refactor code. Using an Enum to define token types offers several advantages: better readability, improved maintainability, and enhanced type safety. Here's how I defined the token types using an Enum:

from enum import Enum, auto

class Spec(Enum):
    OP = auto()
    NUMBER = auto()
    COMMA = auto()
    LPAREN = auto()
    RPAREN = auto()
    GIBBERISH = auto()

By using Spec.OP, Spec.NUMBER, etc., we avoid the ambiguity and potential errors associated with using plain strings.

To seamlessly integrate Enum with funcparserlib, I created a custom decorator named TokenSpec_. This decorator acts as a wrapper around the original TokenSpec function from funcparserlib. It simplifies token definition by accepting a value from our Spec Enum as the spec argument. Internally, it extracts the string representation of the enum (spec.name) and passes that along with any other arguments to the original TokenSpec function.

from enum import Enum, auto

class Spec(Enum):
    OP = auto()
    NUMBER = auto()
    COMMA = auto()
    LPAREN = auto()
    RPAREN = auto()
    GIBBERISH = auto()

With the decorated TokenSpec_ function, this allows us to define the tokenizer. We use make_tokenizer from funcparserlib to create a tokenizer that takes a list of TokenSpec_ definitions. Each definition specifies a token type (from our Spec ENUM) and a regular expression to match it.

from funcparserlib.lexer import TokenSpec

def TokenSpec_(spec: Spec, *args: Any, **kwargs: Any) -> TokenSpec:
    return TokenSpec(spec.name, *args, **kwargs)

The OP regular expression uses alternation (|) to match the different function formats. Specifically:

• mul(?=(d{1,3},d{1,3})): Matches mul only if it's followed by parentheses containing two numbers separated by a comma. The positive lookahead assertion (?=...) ensures that the parentheses and numbers are present but are not consumed by the match.
• do(?=()): Matches do only if followed by empty parentheses.
• don't(?=()): Matches don't only if followed by empty parentheses.

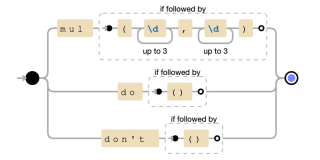
A graph representation of the regular expression

Finally, the tokenize function filters out any GIBBERISH tokens during tokenization to focus on the relevant parts of the input for further processing.

The process of interpreting code typically involves two main stages: lexical analysis (or lexing) and parsing. We’ve already implemented the first stage: our tokenize function acts as a lexer, taking the input string and converting it into a sequence of tokens. These tokens are the fundamental building blocks that the parser will use to understand the structure and meaning of the code. Now, let's explore how the parser uses these tokens.

Implementing the parser

The parsed tokens returned by the tokenize function are then sent to a parser for further processing. To bridge the gap between our Spec Enum and the tok function, we introduce a decorator named tok_.

from funcparserlib.lexer import make_tokenizer

def tokenize(input: str) -> tuple[Token, ...]:
    tokenizer = make_tokenizer(
        [
            TokenSpec_(
                Spec.OP, r"mul(?=\(\d{1,3},\d{1,3}\))|do(?=\(\))|don\'t(?=\(\))"
            ),
            TokenSpec_(Spec.NUMBER, r"\d{1,3}"),
            TokenSpec_(Spec.LPAREN, r"\("),
            TokenSpec_(Spec.RPAREN, r"\)"),
            TokenSpec_(Spec.COMMA, r","),
            TokenSpec_(Spec.GIBBERISH, r"[\s\S]"),
        ]
    )

    return tuple(
        token for token in tokenizer(input) if token.type != Spec.GIBBERISH.name
    )

For example, if we have a Spec.NUMBER token, the returned parser will accept the token, and return a value, as follows:

from funcparserlib.parser import tok

def tok_(spec: Spec, *args: Any, **kwargs: Any) -> Parser[Token, str]:
    return tok(spec.name, *args, **kwargs)

The returned value can then be transformed into the desired data type using the >> operator, as shown below:

from enum import Enum, auto

class Spec(Enum):
    OP = auto()
    NUMBER = auto()
    COMMA = auto()
    LPAREN = auto()
    RPAREN = auto()
    GIBBERISH = auto()

Typically, it’s best practice to use ast.literal_eval when parsing unknown input to avoid potential security vulnerabilities. However, the constraints of this particular Advent of Code puzzle—specifically, that all numbers are valid integers—allow us to use the more direct and efficient int function for converting string representations to integers.

from funcparserlib.lexer import TokenSpec

def TokenSpec_(spec: Spec, *args: Any, **kwargs: Any) -> TokenSpec:
    return TokenSpec(spec.name, *args, **kwargs)

We can define parsing rules to enforce specific token sequences and transform them into meaningful objects. For example, to parse a mul function call, we require the following sequence: left parenthesis, number, comma, another number, right parenthesis. We then transform this sequence into a Mul object:

from funcparserlib.lexer import make_tokenizer

def tokenize(input: str) -> tuple[Token, ...]:
    tokenizer = make_tokenizer(
        [
            TokenSpec_(
                Spec.OP, r"mul(?=\(\d{1,3},\d{1,3}\))|do(?=\(\))|don\'t(?=\(\))"
            ),
            TokenSpec_(Spec.NUMBER, r"\d{1,3}"),
            TokenSpec_(Spec.LPAREN, r"\("),
            TokenSpec_(Spec.RPAREN, r"\)"),
            TokenSpec_(Spec.COMMA, r","),
            TokenSpec_(Spec.GIBBERISH, r"[\s\S]"),
        ]
    )

    return tuple(
        token for token in tokenizer(input) if token.type != Spec.GIBBERISH.name
    )

This rule combines the tok_ parsers for the required tokens (OP, LPAREN, COMMA, RPAREN) with the number parser. The >> operator then transforms the matched sequence into a Mul object, extracting the two numbers from the tuple elem at indices 2 and 4.

We can apply the same principle to define parsing rules for the do and don't operations. These operations take no arguments (represented by empty parentheses) and are transformed into Condition objects:

from funcparserlib.parser import tok

def tok_(spec: Spec, *args: Any, **kwargs: Any) -> Parser[Token, str]:
    return tok(spec.name, *args, **kwargs)

The do rule creates a Condition object with can_proceed = True, while the don't rule creates one with can_proceed = False.

Finally, we combine these individual parsing rules (do, don't, and mul) into a single expr parser using the | (or) operator:

>>> from funcparserlib.lexer import Token
>>> number_parser = tok_(Spec.NUMBER)
>>> number_parser.parse([Token(Spec.NUMBER.name, '123'])
'123'

This expr parser will attempt to match the input against each of the rules in turn, returning the result of the first successful match.

Our expr parser handles complete expressions like mul(2,3), do(), and don't(). However, the input might also contain individual tokens that are not part of these structured expressions. To handle these, we define a catch-all parser called everything:

>>> from funcparserlib.lexer import Token
>>> from ast import literal_eval
>>> number_parser = tok_(Spec.NUMBER) >> literal_eval
>>> number_parser.parse([Token(Spec.NUMBER.name, '123'])
123

This parser uses the | (or) operator to match any single token of type NUMBER, LPAREN, RPAREN, or COMMA. It's essentially a way to capture any stray tokens that aren't part of a larger expression.

With all the components defined, we can now define what constitutes a complete program. A program consists of one or more “calls,” where a “call” is an expression potentially surrounded by stray tokens.

The call parser handles this structure: it matches any number of stray tokens (many(everything)), followed by a single expression (expr), followed by any number of additional stray tokens. The operator.itemgetter(1) function then extracts the matched expression from the resulting sequence.

number = tok_(Spec.NUMBER) >> int

A full program, represented by the program parser, consists of zero or more calls, ensuring that the entire input is consumed by using the finished parser. The parsed result is then converted into a tuple of expressions.

from enum import Enum, auto

class Spec(Enum):
    OP = auto()
    NUMBER = auto()
    COMMA = auto()
    LPAREN = auto()
    RPAREN = auto()
    GIBBERISH = auto()

Finally, we group all these definitions into a parse function. This function takes a tuple of tokens as input and returns a tuple of parsed expressions. All the parsers are defined within the function body to prevent polluting the global namespace and because the number parser depends on the tok_ function.

from funcparserlib.lexer import TokenSpec

def TokenSpec_(spec: Spec, *args: Any, **kwargs: Any) -> TokenSpec:
    return TokenSpec(spec.name, *args, **kwargs)

Solving the puzzle

With our parser in place, solving Part 1 is straightforward. We need to find all mul operations, perform the multiplications, and sum the results. We start by defining an evaluation function that handles Mul expressions

from funcparserlib.lexer import make_tokenizer

def tokenize(input: str) -> tuple[Token, ...]:
    tokenizer = make_tokenizer(
        [
            TokenSpec_(
                Spec.OP, r"mul(?=\(\d{1,3},\d{1,3}\))|do(?=\(\))|don\'t(?=\(\))"
            ),
            TokenSpec_(Spec.NUMBER, r"\d{1,3}"),
            TokenSpec_(Spec.LPAREN, r"\("),
            TokenSpec_(Spec.RPAREN, r"\)"),
            TokenSpec_(Spec.COMMA, r","),
            TokenSpec_(Spec.GIBBERISH, r"[\s\S]"),
        ]
    )

    return tuple(
        token for token in tokenizer(input) if token.type != Spec.GIBBERISH.name
    )

To solve Part 1, we tokenize and parse the input, then use the function evaluate_skip_condition we just defined to get the final result:

from funcparserlib.parser import tok

def tok_(spec: Spec, *args: Any, **kwargs: Any) -> Parser[Token, str]:
    return tok(spec.name, *args, **kwargs)

For Part 2, we need to skip evaluating mul operations if a don't condition has been encountered. We define a new evaluation function, evaluate_with_condition, to handle this:

>>> from funcparserlib.lexer import Token
>>> number_parser = tok_(Spec.NUMBER)
>>> number_parser.parse([Token(Spec.NUMBER.name, '123'])
'123'

This function uses reduce with a custom reducer function to maintain a running sum and a boolean flag (condition). The condition flag is updated when a Condition expression (do or don't) is encountered. Mul expressions are only evaluated and added to the sum if the condition is True.

Previous Iteration

Initially, my approach to parsing involved two distinct passes. First, I would tokenize the entire input string, collecting all tokens regardless of their type. Then, in a separate step, I would perform a second tokenization and parsing specifically to identify and process mul operations.

>>> from funcparserlib.lexer import Token
>>> from ast import literal_eval
>>> number_parser = tok_(Spec.NUMBER) >> literal_eval
>>> number_parser.parse([Token(Spec.NUMBER.name, '123'])
123

The improved approach eliminates this redundancy by performing the tokenization and parsing in a single pass. We now have a single parser that handles all token types, including those related to mul, do, don't, and other individual tokens.

number = tok_(Spec.NUMBER) >> int

Instead of re-tokenizing the input to find mul operations, we leverage the token types identified during the initial tokenization. The parse function now uses these token types to directly construct the appropriate expression objects (Mul, Condition, etc.). This avoids the redundant scanning of the input and significantly improves efficiency.

That wraps up our parsing adventure for this week’s Advent of Code. While this post required a significant time commitment, the process of revisiting and solidifying my knowledge of lexing and parsing made it a worthwhile endeavour. This was a fun and insightful puzzle, and I’m eager to tackle more complex challenges in the coming weeks and share my learnings.

As always, thank you for reading, and I shall write again, next week.

The above is the detailed content of How to parse computer code, Advent of Code ay 3. For more information, please follow other related articles on the PHP Chinese website!