Understanding Big O Notation and Time Complexity in JavaScript

When working with JavaScript, writing functional code is important, but ensuring it runs efficiently is equally crucial. This is where Big O Notation comes in. It provides a way to analyze how your code's performance scales as the size of the input increases, helping you write optimized and scalable applications.

This article will explore the basics of Big O Notation and common time complexities with beginner-friendly examples in JavaScript

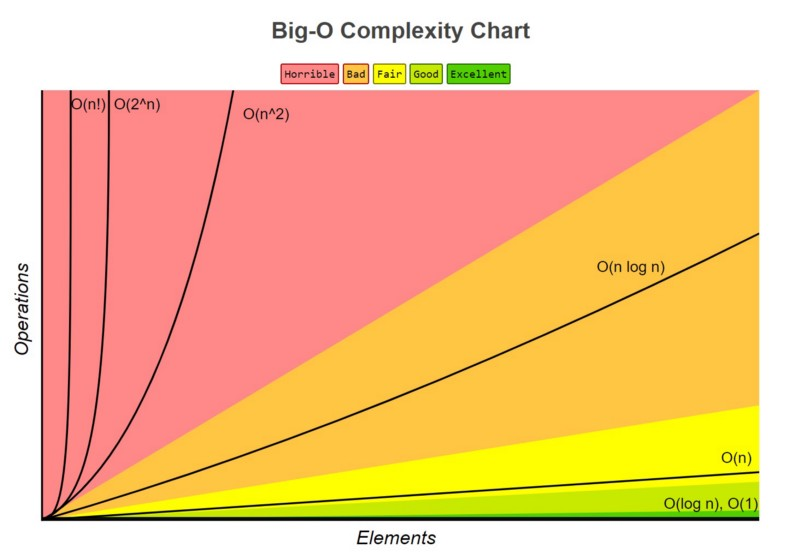
What is Big O Notation?

Big O Notation is a mathematical representation that describes the efficiency of an algorithm. It helps us understand:

1. Time Complexity: How the execution time of an algorithm changes with the size of the input.
2. Space Complexity: How the memory usage of an algorithm changes with the size of the input.

The goal is to evaluate how well an algorithm performs as the input size grows, focusing on worst-case scenarios.

---

Why Does Big O Notation Matter?

Let’s say you’re tasked with finding a name in a phone book:

• One approach is to flip through every page until you find the name (linear search).
• Another is to start in the middle and systematically narrow down (binary search).

Both approaches solve the problem, but their efficiency varies significantly as the size of the phone book grows. Big O helps us compare these approaches and choose the best one.

---

Big O Notation in Action

Below are common Big O complexities, explained with practical examples in JavaScript.

---

1. O(1) - Constant Time

The runtime remains the same regardless of the input size. These operations are the most efficient.

Example: Accessing an element in an array by index.

const numbers = [10, 20, 30, 40, 50];
console.log(numbers[2]); // Always takes the same time, no matter the array size

---

2. O(log n) - Logarithmic Time

The runtime grows logarithmically as the input size increases. This often occurs in divide-and-conquer algorithms like binary search.

Example: Binary search on a sorted array.

function binarySearch(arr, target) {
    let start = 0;
    let end = arr.length - 1;

    while (start <= end) {
        const mid = Math.floor((start + end) / 2);

        if (arr[mid] === target) {
            return mid;
        } else if (arr[mid] < target) {
            start = mid + 1; // Search the right half
        } else {
            end = mid - 1; // Search the left half
        }
    }

    return -1; // Target not found
}

const arr = [1, 3, 5, 7, 9];
console.log(binarySearch(arr, 7)); // Output: 3

---

3. O(n) - Linear Time

The runtime grows proportionally to the input size. This occurs when you need to examine each element once.

Example: Finding an item in an unsorted array.

function linearSearch(arr, target) {
    for (let i = 0; i < arr.length; i++) {
        if (arr[i] === target) {
            return i; // Found
        }
    }
    return -1; // Not found
}

const items = [10, 20, 30, 40, 50];
console.log(linearSearch(items, 30)); // Output: 2

---

4. O(n²) - Quadratic Time

The runtime grows quadratically as the input size increases. This is typical in algorithms with nested loops.

Example: A basic bubble sort implementation.

const numbers = [10, 20, 30, 40, 50];
console.log(numbers[2]); // Always takes the same time, no matter the array size

---

5. O(2ⁿ) - Exponential Time

The runtime doubles with each additional input. This happens in algorithms that solve problems recursively, considering all possible solutions.

Example: Calculating Fibonacci numbers recursively.

function binarySearch(arr, target) {
    let start = 0;
    let end = arr.length - 1;

    while (start <= end) {
        const mid = Math.floor((start + end) / 2);

        if (arr[mid] === target) {
            return mid;
        } else if (arr[mid] < target) {
            start = mid + 1; // Search the right half
        } else {
            end = mid - 1; // Search the left half
        }
    }

    return -1; // Target not found
}

const arr = [1, 3, 5, 7, 9];
console.log(binarySearch(arr, 7)); // Output: 3

---

Visualizing Big O

Here’s how different Big O complexities compare as input size increases:

Big O	Name	Example Use Case	Growth Rate
O(1)	Constant	Array access	Flat
O(log n)	Logarithmic	Binary search	Slow growth
O(n)	Linear	Looping through an array	Moderate growth
O(n²)	Quadratic	Nested loops	Rapid growth
O(2ⁿ)	Exponential	Recursive brute force	Very fast growth

---

Illustration of Growth Rates

Imagine you’re solving a problem, and the input size grows. Here’s how algorithms with different complexities scale as the input size increases:

Input Size	O(1)	O(log n)	O(n)	O(n²)	O(2ⁿ)
1	1 ms	1 ms	1 ms	1 ms	1 ms
10	1 ms	3 ms	10 ms	100 ms	~1 sec
100	1 ms	7 ms	100 ms	10 sec	~centuries
1000	1 ms	10 ms	1 sec	~17 min	Unrealistic

• O(1) stays constant regardless of the input.
• O(log n) grows slowly, ideal for large inputs.
• O(n) grows proportionally to input size.
• O(n²) and higher quickly become impractical for large inputs.

---

Visualizing Big O with Code

Here's how to visualize the number of operations for different complexities using simple counters:

const numbers = [10, 20, 30, 40, 50];
console.log(numbers[2]); // Always takes the same time, no matter the array size

---

Common Misunderstandings About Big O

1. Big O ≠ Actual Performance: Big O tells you how performance scales, not the exact time taken.
   • For example, an O(n) algorithm with a small constant factor may outperform an O(log n) algorithm for small input sizes.
2. Best-Case vs. Worst-Case: Big O usually describes the worst-case scenario. For example, searching for an item not in the list.
3. Not All Nested Loops Are O(n²): The complexity depends on how many elements the inner loop processes.

---

Practical Tips for Beginners

1. Focus on O(1), O(n), and O(n²): These are the most common complexities you'll encounter.
2. Measure Performance: Use tools like Chrome DevTools to benchmark your code.
3. Refactor for Efficiency: Once your code works, identify parts with higher complexities and optimize.
4. Keep Learning: Platforms like LeetCode and HackerRank provide great exercises for understanding Big O.

---

Conclusion

Big O Notation is an essential tool for evaluating the efficiency of algorithms and understanding how your code scales. By grasping the basics and analyzing common patterns, you'll be well on your way to writing performant JavaScript applications.

Happy coding! ?

The above is the detailed content of Understanding Big O Notation and Time Complexity in JavaScript. For more information, please follow other related articles on the PHP Chinese website!