 Technology peripherals
Technology peripherals AI
AI Why didn't I know when I was learning line generation: There is an equivalence relationship between matrices and graphs?
Why didn't I know when I was learning line generation: There is an equivalence relationship between matrices and graphs?Why didn't I know when I was learning line generation: There is an equivalence relationship between matrices and graphs?
The matrix is difficult to understand, but it may be different from another perspective.
When learning mathematics, we are often frustrated by the difficulty and abstractness of the knowledge we learn; but sometimes, just by changing the perspective, we can find a simple and intuitive solution to the problem. For example, when we were learning the formula of sum of squares (a+b)² when we were children, we may not understand why it is equal to a²+2ab+b². We only know that it is written like this in the book and the teacher asked us to remember it like this; until one day we see I saw this animated picture:

I suddenly realized that we can understand it from a geometric perspective!
Now, this sense of enlightenment appears again: the non-negative matrix can be equivalently converted into the corresponding directed graph!
As shown in the figure below, the 3×3 matrix on the left can actually be equivalently represented as a directed graph containing three nodes on the right, and this representation is very helpful for both matrix and graph theory.

This example comes from mathematician Tivadar Danka who is committed to making math accessible for everyone. The self-proclaimed "chaotic good" mathematician vividly introduced this equivalence of matrices and graphs and their uses in a series of tweets and blog posts. To date, the tweets have been read more than 2 million times, garnered more than 3,200 retweets and 9,100 favorites.

The valence of matrices and directed graphs

As shown in the example above, if we treat each row as a node, then each element can be represented as a directed and weighted edges. Of course, 0 elements can be ignored. If the element is located at row i and column j, it corresponds to the edge from node i to node j.
This may seem complicated at first glance, but we can look at one of the nodes first.

As shown in the figure, for this 3×3 matrix, row 1 corresponds to the topmost node (we call it node 1 here), which contains 3 elements but one of them is 0, so This node extends two edges. The yellow edge represents the element 0.5 at (1,1), so it is a directed edge pointing to itself with a weight of 0.5. Similarly, the blue edge is the edge that points to node 2 and has a weight of 1.
In this way, we can analyze that the i-th column of the matrix corresponds to all edges pointing to the i-th node.

What is the use of this equivalent expression?
This equivalence between non-negative matrices and directed graphs can not only help us better understand matrices and their operations, but also help simplify some calculation processes; in turn, this can also help us start from a new perspective Comprehension diagram.
For example, the power of the matrix corresponds to the walk in the graph.

As shown in the figure above, for the k-th power of the n×n square matrix A, the summation process of each element will incorporate all possible k-step walks.
For example, suppose we want to calculate the square of the above 3×3 matrix.

If we use matrix multiplication, we need to calculate it like this:

For the first element of the operation result, we can get the result = 0.5×0.5+1×0.2+0×1.8 = 0.45. Finally, we can get the complete result as:

But if we use the above graph walking method, we can get the result by walking the path. Likewise, for the first element of the result matrix, we need to sum up all 2-step walking paths that satisfy a_{1,l}→a_{l,1}.
However, if this directed graph represents the state of a Markov chain, the square of its transition probability matrix essentially represents the probability of the chain reaching a certain state after 2 steps.
Not only that, using graphs to represent matrices can also give us an in-depth understanding of the structure of non-negative matrices. To do this, Danka said we need to first understand the concept of "strongly connected components."
Strongly connected component
What is a strongly connected component? For a directed graph, if every other node in the graph can be reached from every node, we say that the graph is strongly connected. As shown below.

The strongly connected component refers to the part/subgraph in the directed graph that can achieve strong connectivity. As shown in the figure below, there is a strongly connected component on the left and right, while the white edge in the middle does not belong to any strongly connected component.

The figure below shows another example, where the yellow part is the strongly connected component:

The matrix corresponding to the strongly connected graph is an irreducible matrix, while all other matrices in the non-negative matrix are reducible matrix.

Danka explains with an example. (For the sake of simplicity, all the weights in the example are unit weights, but in practice these weight values can be any non-negative values.)
Let’s transcribe this graph that contains strongly connected components but is not strongly connected itself into the corresponding Matrix form:

And this matrix is a reducible matrix.

It can be seen that the two submatrices on the main diagonal represent two strongly connected components respectively, and the submatrix on the upper right represents the edge from the first strongly connected component to the second strongly connected component , the one on the lower left represents the edge from the second strongly connected component to the first strongly connected component (because there is no such edge, all are 0).
This form of writing a block matrix is called Frobenius normal form.

So, we naturally ask: Can we convert any non-negative matrix into a Frobenius normal form matrix?
By using a directed graph to represent a non-negative matrix, we can easily see that the answer is yes, because any directed graph representing a non-negative matrix can be represented as strongly connected components that are connected to each other. This process is very simple:
Construct the corresponding directed graph for the non-negative matrix;
Find the strongly connected components;
Change to a better way to label each node.
That’s it!
Use pictures to get the Frobenius standard form
So, what is this better way?
Based on the above example, let’s take a look at the process.
First, fuse each strongly connected component into a single object, as shown in the figure below. At this time, we can treat each strongly connected component as a black box - we don't care about its internal structure, only its external connections.

Then, in this new graph, we need to find the components that have only outgoing edges but no incoming edges. There is only one in this specific example, and we label it number 0:

The next step is more troublesome: number each component so that the number of each component is the furthest distance from number 0. The following example can illustrate this point more clearly:

You can see that there are two paths from No. 0 to the middle component, so choose the path farthest from 0 to number it. Finally got:

Actually, this defines the order of components. Next, mark the internal nodes of each component:

If the graph itself comes from a matrix, then such a re-labeling process can result in a Frobe Nius canonical form matrix!

In fact, this re-labeling process is to use a permutation matrix P to transform the original matrix, and the permutation matrix is composed of multiple transpose matrices The product composition.

The following is the full form of the theorem:

Of course, The uses of using graphs to represent matrices go far beyond this. For example, we can also use the eigenvalues of the matrix to define the eigenvalues of the graph. In fact, this line of thinking gave rise to the research field of spectral graph theory.
Conclusion
Obviously, this equivalence relationship between matrices and graphs is not only helpful for graph theory research, but also for Linear algebra provides a new perspective on calculations and analysis. It also has some important practical uses. For example, DNA data is often represented in the form of matrices or graphs.
In addition, we all know the importance of matrix operations for current large-model AI, and graphs represented by knowledge graphs are also becoming an important driver of current AI through technologies such as retrieval-enhanced search. Connecting the two may bring some new breakthroughs in AI interpretability and graph artificial intelligence. At the very least, this helps us learn linear algebra better.
In fact, the above content is extracted from the book "Mathematics of Machine Learning" being written by Tivadar Danka. This book will introduce the mathematical knowledge related to machine learning from a simple to a deep level, allowing readers to truly understand what is happening and why. Danka confidently declares that this will be "the best resource for learning machine learning." At present, he has released two chapter previews online. Interested readers can visit: https://tivadardanka.com/mathematics-of-machine-learning-preview/
The above is the detailed content of Why didn't I know when I was learning line generation: There is an equivalence relationship between matrices and graphs?. For more information, please follow other related articles on the PHP Chinese website!
 How to Optimize Data Warehouse with STAR Schema?Apr 12, 2025 am 09:33 AM
How to Optimize Data Warehouse with STAR Schema?Apr 12, 2025 am 09:33 AMThe STAR schema is an efficient database design used in data warehousing and business intelligence. It organizes data into a central fact table linked to surrounding dimension tables. This star-like structure simplifies complex q
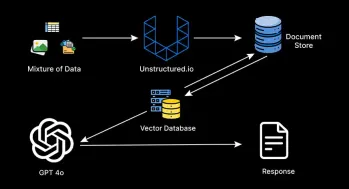 A Comprehensive Guide to Building Multimodal RAG SystemsApr 12, 2025 am 09:29 AM
A Comprehensive Guide to Building Multimodal RAG SystemsApr 12, 2025 am 09:29 AMRetrieval Augmented Generation systems, better known as RAG systems, have become the de-facto standard for building intelligent AI assistants answering questions on custom enterprise data without the hassles of expensive fine-tun
 How Agentic RAG Systems Transform Tech?Apr 12, 2025 am 09:21 AM
How Agentic RAG Systems Transform Tech?Apr 12, 2025 am 09:21 AMIntroduction Artificial Intelligence has entered a new era. Gone are the days when models would simply output information based on predefined rules. The cutting-edge approach in AI today revolves around RAG (Retrieval-Augmente
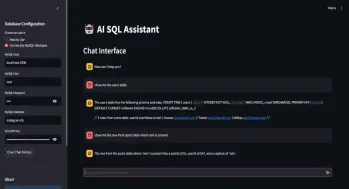 SQL Assistant to Auto-Generate QueriesApr 12, 2025 am 09:13 AM
SQL Assistant to Auto-Generate QueriesApr 12, 2025 am 09:13 AMHave you ever wished you could simply talk to your database, ask questions in plain language, and get instant answers without writing complex SQL queries or sorting through spreadsheets? With LangChain’s SQL toolkit, GROQ A
 Reading The AI Index 2025: Is AI Your Friend, Foe, Or Co-Pilot?Apr 11, 2025 pm 12:13 PM
Reading The AI Index 2025: Is AI Your Friend, Foe, Or Co-Pilot?Apr 11, 2025 pm 12:13 PMThe 2025 Artificial Intelligence Index Report released by the Stanford University Institute for Human-Oriented Artificial Intelligence provides a good overview of the ongoing artificial intelligence revolution. Let’s interpret it in four simple concepts: cognition (understand what is happening), appreciation (seeing benefits), acceptance (face challenges), and responsibility (find our responsibilities). Cognition: Artificial intelligence is everywhere and is developing rapidly We need to be keenly aware of how quickly artificial intelligence is developing and spreading. Artificial intelligence systems are constantly improving, achieving excellent results in math and complex thinking tests, and just a year ago they failed miserably in these tests. Imagine AI solving complex coding problems or graduate-level scientific problems – since 2023
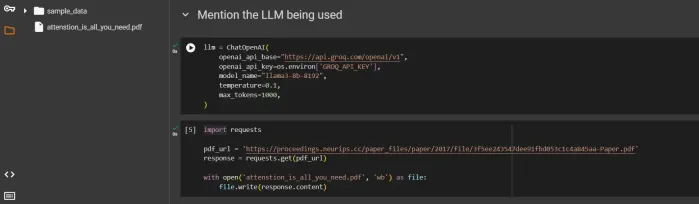
 Getting Started With Meta Llama 3.2 - Analytics VidhyaApr 11, 2025 pm 12:04 PM
Getting Started With Meta Llama 3.2 - Analytics VidhyaApr 11, 2025 pm 12:04 PMMeta's Llama 3.2: A Leap Forward in Multimodal and Mobile AI Meta recently unveiled Llama 3.2, a significant advancement in AI featuring powerful vision capabilities and lightweight text models optimized for mobile devices. Building on the success o
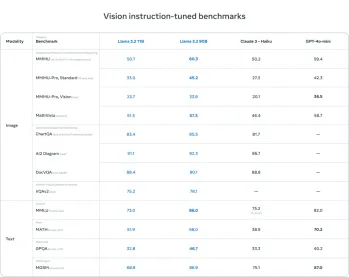 AV Bytes: Meta's Llama 3.2, Google's Gemini 1.5, and MoreApr 11, 2025 pm 12:01 PM
AV Bytes: Meta's Llama 3.2, Google's Gemini 1.5, and MoreApr 11, 2025 pm 12:01 PMThis week's AI landscape: A whirlwind of advancements, ethical considerations, and regulatory debates. Major players like OpenAI, Google, Meta, and Microsoft have unleashed a torrent of updates, from groundbreaking new models to crucial shifts in le
 The Human Cost Of Talking To Machines: Can A Chatbot Really Care?Apr 11, 2025 pm 12:00 PM
The Human Cost Of Talking To Machines: Can A Chatbot Really Care?Apr 11, 2025 pm 12:00 PMThe comforting illusion of connection: Are we truly flourishing in our relationships with AI? This question challenged the optimistic tone of MIT Media Lab's "Advancing Humans with AI (AHA)" symposium. While the event showcased cutting-edg


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Atom editor mac version download
The most popular open source editor

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.




