 Technology peripherals
Technology peripherals AI
AI Complete 1 year MD calculation in 2.5 days? DeepMind team's new calculation method based on Euclidean Transformer
Complete 1 year MD calculation in 2.5 days? DeepMind team's new calculation method based on Euclidean TransformerComplete 1 year MD calculation in 2.5 days? DeepMind team's new calculation method based on Euclidean Transformer

Editor | Carrot Skin
In recent years, great progress has been made in the development of machine learning force fields (MLFF) based on ab initio reference calculations. Although low test errors are achieved, the reliability of MLFF in molecular dynamics (MD) simulations is facing increasing scrutiny due to concerns about instability over longer simulation time scales.
Research has shown a potential link between robustness to cumulative inaccuracies and the use of equivariant representations in MLFF, but the computational costs associated with these representations may limit this advantage in practice.
To solve this problem, researchers from Google DeepMind and TU Berlin proposed a transformer architecture called SO3krates, which combines sparse equivariant representation (Euclidean variables) with separation invariant and equivariant It combines a self-attention mechanism with variable information, eliminating the need for expensive tensor products.
SO3krates achieve a unique combination of precision, stability and speed, enabling in-depth analysis of the quantum properties of matter over long time periods and system scales.
The research was titled "A Euclidean transformer for fast and stable machine learned force fields" and was published in "Nature Communications" on August 6, 2024.

Background and Challenges
Molecular dynamics (MD) simulation can reveal the evolution of the system from microscopic interactions to macroscopic properties through long-term simulations, and its prediction accuracy depends on the interatomic interactions that drive the simulation. force accuracy. Traditionally, these forces have been derived from approximate force fields (FF) or computationally complex ab initio electronic structure methods.
In recent years, machine learning (ML) potential energy models have provided more flexible prediction methods by exploiting the statistical dependence of molecular systems.
However, studies have shown that the test error of ML models on benchmark datasets is weakly correlated with performance in long-term MD simulations.
To improve extrapolation performance, complex architectures such as message passing neural networks (MPNNs) have been developed, especially equivariant MPNNs, which capture the direction information between atoms by introducing tensor products to improve data transferability.
In the SO(3) equivariant architecture, the convolution is performed on the SO(3) rotation group based on spherical harmonics. By fixing the maximum degree  of the spherical harmonics in the architecture, exponential growth of the associated function space can be avoided.
of the spherical harmonics in the architecture, exponential growth of the associated function space can be avoided.
Scientists have proven that the maximum order is closely related to accuracy, data efficiency, and related to the reliability of the model in MD simulations. However, SO(3) convolutions scale  , which can increase the prediction time per conformation by up to two orders of magnitude compared to the invariant model.
, which can increase the prediction time per conformation by up to two orders of magnitude compared to the invariant model.
This leads to a situation where compromises must be made between accuracy, stability and speed, and can also create significant practical problems. These issues must be addressed before these models can be useful in high-throughput or broad-based exploration missions.
A new method with powerful performance
The research team of Google DeepMind and the Technical University of Berlin used this as a motivation to propose a Euclidean self-attention mechanism, using the relative directions of atomic neighborhoods filters instead of SO(3) convolutions, thereby representing atomic interactions without expensive tensor products; the method is called SO3krates.

Illustration: SO3krates architecture and building blocks. (Source: Paper)
This solution builds on recent advances in neural network architecture design and geometric deep learning. SO3krates uses sparse representations for molecular geometries and restricts the projection of all convolution responses to the most relevant invariant components of the equivariant basis functions.

Illustration: Learning invariants. (Source: paper)
Due to the orthogonality of spherical harmonics, this projection corresponds to the trace of the product tensor, which can be represented by a linearly scaled inner product. This can be efficiently extended to higher-order equivariant representations without sacrificing computational speed or memory cost.
Force predictions are derived from the gradient of the resulting invariant energy model, which represents a piecewise linearization of natural equivariants. Throughout the process, self-attention mechanisms are used to separate invariant and equivariant basic elements in the model.
The team compared the stability and speed of the SO3krates model with current state-of-the-art ML models and found that the solution overcomes the limitations of current equivariant MLFFs without compromising their advantages.
The mathematical formula proposed by the researchers can realize an efficient equivariant architecture, thereby achieving reliable and stable MD simulation; compared with the equivariant MPNN with comparable stability and accuracy, its speed can be increased by about 30 times.
To prove this, the researchers ran precise nanosecond-scale MD simulations of supramolecular structures in just a few hours, allowing them to calculate the range from a small peptide with 42 atoms to a peptide with 370 atoms. Fourier transform of the convergence rate autocorrelation function of the nanostructured structure.

Graphic: Overview of results. (Source: Paper)
The researchers further applied this model to explore the PES topology of docosahexaenoic acid (DHA) and Ac-Ala3-NHMe by studying 10k minima using a minimum hopping algorithm.
Such a study would require approximately 30M FF evaluations performed at temperatures between a few hundred K and 1200 K. Using DFT methods, this analysis requires more than a year of computational time. Existing equivariant MLFF with similar prediction accuracy would take more than a month to run to complete such an analysis.
In comparison, the team was able to complete the simulation in just 2.5 days, making it possible to explore hundreds of thousands of PES minima on realistic time scales.
In addition, SO3krates is able to detect physically valid minimum conformations that are not included in the training data. The ability to extrapolate to unknown parts of PES is critical for scaling MLFF to large structures, since available ab initio reference data only cover subregions of conformationally rich structures.
The team also studied the impact of disabling the equal variance property in the network architecture to gain a deeper understanding of its impact on model properties and its reliability in MD simulations.
The researchers found that equivariance is related to the stability of the resulting MD simulations and the extrapolation behavior to higher temperatures. It can be shown that even if the test error estimates are the same on average, equivariance reduces the spread of the error distribution.

Thus, using directional information via equivariant representation is similar in spirit to classical ML theory, where mapping to higher dimensions can yield richer feature spaces that are easier to parameterize.
Future Research
In a series of recent studies, methods aimed at reducing the computational complexity of SO(3) convolutions have been proposed. They can serve as a replacement for full SO(3) convolutions, and the method presented in this article can completely avoid the use of expensive SO(3) convolutions in the message passing paradigm.
These results all indicate that the optimization of equivariant interactions is an active research area that is not yet fully mature and may provide avenues for further improvements.

While the team’s work makes it possible to achieve stable extended simulation timescales using the modern MLFF modeling paradigm, future optimizations are still needed to bring the applicability of MLFF closer to traditional classic FF.
Currently, various promising avenues have emerged in this direction: In current designs, EVs are defined solely in terms of two-body interactions. The accuracy can be further improved by incorporating atomic cluster expansion into the MP step. At the same time, this may help reduce the number of MP steps and thus the computational complexity of the model.
Another issue that has not yet been discussed is the proper handling of global effects. By using low-rank approximations, trainable Ewald summation, or by learning long-range corrections in a physically inspired way. The latter type of approach is particularly important when extrapolation to larger systems is required.
While equivariant models can improve extrapolation of local interactions, this does not apply to interactions beyond the length scales present in the training data or beyond the effective cutoff of the model.
Since the above methods rely on local properties such as partial charge, electronegativity or Hirshfield volume, they can be seamlessly integrated into the team’s architecture by learning the corresponding local descriptors in the invariant feature branch of the SO3krates architecture. in method.
Therefore, future work will focus on incorporating many-body expansions, global effects, and long-range interactions into the EV formalism, and aim to further improve computational efficiency and ultimately span MD timescales with high accuracy.
Paper link: https://www.nature.com/articles/s41467-024-50620-6
Related content: https://phys.org/news/2024-08-faster-coupling- ai-fundamental-physics.html
The above is the detailed content of Complete 1 year MD calculation in 2.5 days? DeepMind team's new calculation method based on Euclidean Transformer. For more information, please follow other related articles on the PHP Chinese website!
 Tesla's Robovan Was The Hidden Gem In 2024's Robotaxi TeaserApr 22, 2025 am 11:48 AM
Tesla's Robovan Was The Hidden Gem In 2024's Robotaxi TeaserApr 22, 2025 am 11:48 AMSince 2008, I've championed the shared-ride van—initially dubbed the "robotjitney," later the "vansit"—as the future of urban transportation. I foresee these vehicles as the 21st century's next-generation transit solution, surpas
 Sam's Club Bets On AI To Eliminate Receipt Checks And Enhance RetailApr 22, 2025 am 11:29 AM
Sam's Club Bets On AI To Eliminate Receipt Checks And Enhance RetailApr 22, 2025 am 11:29 AMRevolutionizing the Checkout Experience Sam's Club's innovative "Just Go" system builds on its existing AI-powered "Scan & Go" technology, allowing members to scan purchases via the Sam's Club app during their shopping trip.
 Nvidia's AI Omniverse Expands At GTC 2025Apr 22, 2025 am 11:28 AM
Nvidia's AI Omniverse Expands At GTC 2025Apr 22, 2025 am 11:28 AMNvidia's Enhanced Predictability and New Product Lineup at GTC 2025 Nvidia, a key player in AI infrastructure, is focusing on increased predictability for its clients. This involves consistent product delivery, meeting performance expectations, and
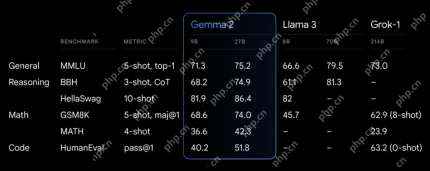 Exploring the Capabilities of Google's Gemma 2 ModelsApr 22, 2025 am 11:26 AM
Exploring the Capabilities of Google's Gemma 2 ModelsApr 22, 2025 am 11:26 AMGoogle's Gemma 2: A Powerful, Efficient Language Model Google's Gemma family of language models, celebrated for efficiency and performance, has expanded with the arrival of Gemma 2. This latest release comprises two models: a 27-billion parameter ver
 The Next Wave of GenAI: Perspectives with Dr. Kirk Borne - Analytics VidhyaApr 22, 2025 am 11:21 AM
The Next Wave of GenAI: Perspectives with Dr. Kirk Borne - Analytics VidhyaApr 22, 2025 am 11:21 AMThis Leading with Data episode features Dr. Kirk Borne, a leading data scientist, astrophysicist, and TEDx speaker. A renowned expert in big data, AI, and machine learning, Dr. Borne offers invaluable insights into the current state and future traje
 AI For Runners And Athletes: We're Making Excellent ProgressApr 22, 2025 am 11:12 AM
AI For Runners And Athletes: We're Making Excellent ProgressApr 22, 2025 am 11:12 AMThere were some very insightful perspectives in this speech—background information about engineering that showed us why artificial intelligence is so good at supporting people’s physical exercise. I will outline a core idea from each contributor’s perspective to demonstrate three design aspects that are an important part of our exploration of the application of artificial intelligence in sports. Edge devices and raw personal data This idea about artificial intelligence actually contains two components—one related to where we place large language models and the other is related to the differences between our human language and the language that our vital signs “express” when measured in real time. Alexander Amini knows a lot about running and tennis, but he still
 Jamie Engstrom On Technology, Talent And Transformation At CaterpillarApr 22, 2025 am 11:10 AM
Jamie Engstrom On Technology, Talent And Transformation At CaterpillarApr 22, 2025 am 11:10 AMCaterpillar's Chief Information Officer and Senior Vice President of IT, Jamie Engstrom, leads a global team of over 2,200 IT professionals across 28 countries. With 26 years at Caterpillar, including four and a half years in her current role, Engst
 New Google Photos Update Makes Any Photo Pop With Ultra HDR QualityApr 22, 2025 am 11:09 AM
New Google Photos Update Makes Any Photo Pop With Ultra HDR QualityApr 22, 2025 am 11:09 AMGoogle Photos' New Ultra HDR Tool: A Quick Guide Enhance your photos with Google Photos' new Ultra HDR tool, transforming standard images into vibrant, high-dynamic-range masterpieces. Ideal for social media, this tool boosts the impact of any photo,


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

Dreamweaver Mac version
Visual web development tools

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software




