 Technology peripherals
Technology peripherals AI
AI A significant breakthrough in the Riemann Hypothesis! Tao Zhexuan strongly recommends new papers from MIT and Oxford, and the 37-year-old Fields Medal winner participated
A significant breakthrough in the Riemann Hypothesis! Tao Zhexuan strongly recommends new papers from MIT and Oxford, and the 37-year-old Fields Medal winner participatedA significant breakthrough in the Riemann Hypothesis! Tao Zhexuan strongly recommends new papers from MIT and Oxford, and the 37-year-old Fields Medal winner participated
Recently, the Riemann Hypothesis, known as one of the seven major problems of the millennium, has reached a new breakthrough.
The Riemann Hypothesis is a very important unsolved problem in mathematics, related to the precise properties of the distribution of prime numbers (primes are those numbers that can only be divided by 1 and themselves, they play a fundamental role in number theory Role).
In today’s mathematical literature, there are more than a thousand mathematical propositions based on the establishment of the Riemann Hypothesis (or its generalized form). In other words, once the Riemann Hypothesis and its generalized form are proven, these more than a thousand propositions will be established as theorems, which will have a profound impact on the field of mathematics; and if the Riemann Hypothesis is proven wrong, then among these propositions part of it will also lose its effectiveness.
The new breakthrough comes from a paper by MIT mathematics professor Larry Guth and Oxford University Institute of Mathematics professor and Fields Medal winner James Maynard. Mathematician Terence Tao, who recommended the paper, said they provided the first substantial improvement on the classic 1940 Ingham bound on the zeros of the Riemannian zeta function (and, more generally, on controlling large values of various Dirichlet series). Previously, the Ingham bound, which was born more than 80 years ago, restricted mathematicians from doing many things in analytic number theory due to lack of improvement.

However, Tao Zhexuan also said that although this is a significant breakthrough, it is still far from completely solving the Riemann Hypothesis, so it should be viewed rationally.
What is the Riemann Hypothesis?
The Riemann Hypothesis or Riemann Hypothesis was proposed by German mathematician Bernhard Riemann in 1859. This conjecture is closely related to the distribution of prime numbers, and its core content involves the non-trivial zeros of the Riemann Zeta Function.

Bernhard Riemann, Source: facts.net/
The content of the Riemann Hypothesis cannot be described by completely elementary mathematics. Roughly speaking, it is a conjecture about a complex variable function called the Riemann zeta function (that is, a function in which both the variable and the function value can take values in the complex domain). The Riemann zeta function, like many other functions, has a value of zero at certain points. Those points are called the zero points of the Riemann zeta function. Among those zeros, there are some particularly important non-trivial zeros called the Riemann zeta function. What the Riemann Hypothesis predicts is that all non-trivial zero points are distributed on a special straight line called the "critical line" (quoted from the blog of popular science writer Lu Changhai).
The Riemann ζ function is defined as:
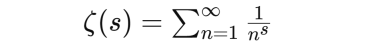
The Riemann Hypothesis holds that the real part of all non-trivial zeros of the ζ function is 1/2. This means that if ζ(s)=0 and s is a non-trivial zero (i.e. s is not negative even), then the real part of s should be 1/2.
The Riemann Hypothesis is the most important and most anticipated mathematical problem in the world today. If the conjecture is true, the distribution of prime numbers among natural numbers can be accurately described, and it will have wide application and influence in solving number theory, complex analysis and other branches of mathematics.
So far, 165 years have passed since the Riemann Hypothesis was proposed. There have been many studies trying to prove the Riemann Hypothesis, but they have all come to nothing.
Attempts to solve the Riemann Hypothesis
Since the Riemann Hypothesis was proposed, many mathematicians have begun a journey of exploring the proof.
In 1896, French mathematicians Jacques Adamard and Charles Jean de la Vallée-Poussin independently proved that there are no zero points on a straight line. Together with other properties that Riemann had proved for non-trivial zeros, this shows that all non-trivial zeros must lie on regions. This is a crucial step in the first complete proof of the prime number theorem.
In 1900, David Hilbert, a German mathematician and one of the fathers of modern mathematics, included the Riemann Hypothesis in his famous 23 questions, and together with Goldbach’s Hypothesis, they formed Hilbert’s list Question No. 8. At the same time, the Riemann Hypothesis is also the only Hilbert problem to be included in the Millennium Prize of the Clay Mathematics Institute.
In 1914, the British mathematician Godfrey Harold Hardy proved that there are infinite zero points on the straight line  . Later, the work of Hardy and the British mathematician John Unther Littlewood in 1921 and Selberg in 1942 (critical line theorem) was to calculate the average density of zero points on the critical line
. Later, the work of Hardy and the British mathematician John Unther Littlewood in 1921 and Selberg in 1942 (critical line theorem) was to calculate the average density of zero points on the critical line  .
.
Until recent years, attempts to prove the Riemann Hypothesis have often caused a stir.
In September 2018, an unprecedented speech in Heidelberg detonated the mathematics circle. The 89-year-old Sir Atiyah’s proof of the Riemann Hypothesis attracted global attention. Under the spotlight, Sir Atiyah spent 45 minutes presenting to the world the proof of this mathematical conjecture that has a history of more than 150 years.
But Sir Atiyah’s proof is only the following page of PPT. Such proof seems unconvincing. When asked whether he had solved the Riemann Hypothesis, he responded, "It depends on your logic. I proved the original Riemann Hypothesis, unless you are the kind of mathematician who does not accept proof by contradiction." He He also added that his proof did not solve all the problems, and there will be many problems in the future. He only took the first step (the first step is the solution).
Sadly, Sir Atiyah passed away in January 2019.

Now, someone else has challenged the Riemann Hypothesis.
What Guth and Maynard did
Regarding Guth and Maynard’s new breakthrough, the well-known mathematician Teresa Tao commented: "Guth and Maynard have made important progress in studying the Riemann Hypothesis, although they are still far from solving this long-standing problem. Mathematics problems still have a long way to go."

Paper link: https://arxiv.org/pdf/2405.20552
We learned from Tao Zhexuan's tweet that this research is the first time for mathematician Albert Ingham. Substantial improvements were made around 1940 on the classical bounds on the zeros of the Riemannian zeta function (and more generally on large values governing various Dirichlet series).
In 1940, mathematician Albert Ingham proposed a bound describing these zero points, which formed the basis for theoretical research at the time. However, until the work of Guth and Maynard, this bound had hardly been refined. Guth and Maynard's research not only improved this bound of Ingham's, but their method provided new tools and perspectives for dealing with large values of Dirichlet series, which are important in many number theory and analytical problems.
This paper proves a new bound on the frequency of large values of Dirichlet polynomials. This provides an improved estimate for a Dirichlet polynomial of length N, with values close to 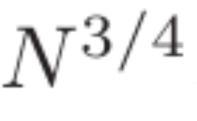 . Furthermore, the study derives a zero-point density estimate
. Furthermore, the study derives a zero-point density estimate 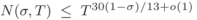 and an asymptotic expression for primes over short intervals of length
and an asymptotic expression for primes over short intervals of length 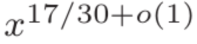 .
.
Tao Zhexuan himself gave some explanations about this research from a mathematical perspective. Let ?(σ,?) denote the number of zeros of the Riemann ζ function where the real part is at least σ and the imaginary part is at most T. The Riemann Hypothesis tells us that N (σ,?) will disappear for any σ>1/2, but this hypothesis cannot be proven yet. But as a second best option, mathematicians can prove a zero-point density estimate, which is a non-trivial upper bound on ?(σ,?) .
It turns out that σ=3/4 is a key value. In 1940, Ingham derived the bound ?(3/4,?)≪?(3/5+?(1)).

Over the next eighty years, improvements to this bound were only minor refinements of ?(1) error. This limits researchers to conduct more in-depth research in analytic number theory: for example, in order to obtain a good prime number theorem in almost all short intervals of the form (?,?+?^?), people have long been limited to ?>1/6 range, the main obstacle is the lack of improvements to the Ingham bounds.

Guth and Maynard finally improved the Ingham boundary from 3/5=0.6 to 13/25=0.52. This has produced many corresponding improvements in analytic number theory. For example, researchers can prove the range of the prime number theorem in almost all short intervals, now from θ>1/6=0.166… to θ>2/15=0.133…

About the author
Larry Guth has served as the Claude E. Shannon Professor of Mathematics at MIT since July 2019 and was elected as a MacVicar Fellow in 2021.
He received his PhD from MIT in 2005 under the supervision of Tom Mrowka. This was followed by a postdoc at Stanford University, a junior faculty position at the University of Toronto, and in 2011 he was appointed Courant Institute Professor. He then joined the MIT Department of Mathematics as a professor in 2012.
Guth’s research interests are metric geometry, harmonic analysis, and extreme value combinations. Metric geometry refers to the study of inequalities involving length, area and volume. Some major examples are isoperimetric inequalities and contraction inequalities. Contraction inequalities were a focus of Guth's work, and another focus was finding connections between geometric inequalities and topology.
Recently, Guth is engaged in research on harmonic analysis and combinatorics. Much work is related to the Kakeya problem, an unsolved problem in Euclidean geometry, to restricted-type estimates in Fourier analysis, and to estimates of line occurrence rates in extremal combinatorics.

Born in 1987, is a British mathematician whose research field is analytic number theory, especially prime number theory.
Some of the most famous problems in number theory relate to the distribution of prime numbers. While the large-scale distribution of prime numbers follows the theorems of number theory (more precisely the Riemann Hypothesis), many natural problems need to deal with short (or sparse) scales.James Maynard achieved important results on the twin prime conjecture in 2013. He proved that there are infinite pairs of prime numbers with intervals less than 600. This result is smaller than Zhang Yitang's 70 million intervals. Although his paper was published half a year later than Zhang Yitang, his results were highly praised among number theory experts.
Tao Zhexuan commented: "To be honest, his way of describing is actually cleaner than mine... It turns out that his statement is slightly stronger." Maynard's method is both elegant and powerful, in a shocking way The method breaks through the boundaries of screening theory. And in a seemingly opposite direction, he went on to show that sometimes primes are much sparser than average, a famous Erdős problem that had not made any substantial progress for decades. Maynard also did fundamental work in the field of Diophantine approximation, solving the Duffin–Schaeffer conjecture with Koukoulopoulos, a professor of mathematics at the University of Montreal. This conjecture, proposed in 1941, can be considered the final generalization of Khintchine's theorem, which describes how a typical real number can be approximated by a rational number. In 2022, Maynard was awarded the Fields Medal for his contributions to analytic number theory. The Fields Medal is the most prestigious award in mathematics and is often considered the Nobel Prize of mathematics. James Maynard is honored for his contributions to analytic number theory, which have led to significant advances in understanding the structure of prime numbers and Diophantine approximation. In 2023, he won another New Horizons Award in Mathematics.Looking forward to the two mathematicians making more progress on world problems such as the Riemann Hypothesis.
Reference link: 
https://www.jiqizhixin.com/articles/2019-01-12
https://www.zhihu.com/tardis/zm/ art/557594612
https://news.mit.edu/2014/profile-larry-guth-0527
https://mathstodon.xyz/@tao/112557248794707738
https://zh.wikipedia.org/wiki/% E9% BB%8E% EBC%9% EBC%8% 9C% E6%83% B3
The above is the detailed content of A significant breakthrough in the Riemann Hypothesis! Tao Zhexuan strongly recommends new papers from MIT and Oxford, and the 37-year-old Fields Medal winner participated. For more information, please follow other related articles on the PHP Chinese website!
 You Must Build Workplace AI Behind A Veil Of IgnoranceApr 29, 2025 am 11:15 AM
You Must Build Workplace AI Behind A Veil Of IgnoranceApr 29, 2025 am 11:15 AMIn John Rawls' seminal 1971 book The Theory of Justice, he proposed a thought experiment that we should take as the core of today's AI design and use decision-making: the veil of ignorance. This philosophy provides a simple tool for understanding equity and also provides a blueprint for leaders to use this understanding to design and implement AI equitably. Imagine that you are making rules for a new society. But there is a premise: you don’t know in advance what role you will play in this society. You may end up being rich or poor, healthy or disabled, belonging to a majority or marginal minority. Operating under this "veil of ignorance" prevents rule makers from making decisions that benefit themselves. On the contrary, people will be more motivated to formulate public
 Decisions, Decisions… Next Steps For Practical Applied AIApr 29, 2025 am 11:14 AM
Decisions, Decisions… Next Steps For Practical Applied AIApr 29, 2025 am 11:14 AMNumerous companies specialize in robotic process automation (RPA), offering bots to automate repetitive tasks—UiPath, Automation Anywhere, Blue Prism, and others. Meanwhile, process mining, orchestration, and intelligent document processing speciali
 The Agents Are Coming – More On What We Will Do Next To AI PartnersApr 29, 2025 am 11:13 AM
The Agents Are Coming – More On What We Will Do Next To AI PartnersApr 29, 2025 am 11:13 AMThe future of AI is moving beyond simple word prediction and conversational simulation; AI agents are emerging, capable of independent action and task completion. This shift is already evident in tools like Anthropic's Claude. AI Agents: Research a
 Why Empathy Is More Important Than Control For Leaders In An AI-Driven FutureApr 29, 2025 am 11:12 AM
Why Empathy Is More Important Than Control For Leaders In An AI-Driven FutureApr 29, 2025 am 11:12 AMRapid technological advancements necessitate a forward-looking perspective on the future of work. What happens when AI transcends mere productivity enhancement and begins shaping our societal structures? Topher McDougal's upcoming book, Gaia Wakes:
 AI For Product Classification: Can Machines Master Tax Law?Apr 29, 2025 am 11:11 AM
AI For Product Classification: Can Machines Master Tax Law?Apr 29, 2025 am 11:11 AMProduct classification, often involving complex codes like "HS 8471.30" from systems such as the Harmonized System (HS), is crucial for international trade and domestic sales. These codes ensure correct tax application, impacting every inv
 Could Data Center Demand Spark A Climate Tech Rebound?Apr 29, 2025 am 11:10 AM
Could Data Center Demand Spark A Climate Tech Rebound?Apr 29, 2025 am 11:10 AMThe future of energy consumption in data centers and climate technology investment This article explores the surge in energy consumption in AI-driven data centers and its impact on climate change, and analyzes innovative solutions and policy recommendations to address this challenge. Challenges of energy demand: Large and ultra-large-scale data centers consume huge power, comparable to the sum of hundreds of thousands of ordinary North American families, and emerging AI ultra-large-scale centers consume dozens of times more power than this. In the first eight months of 2024, Microsoft, Meta, Google and Amazon have invested approximately US$125 billion in the construction and operation of AI data centers (JP Morgan, 2024) (Table 1). Growing energy demand is both a challenge and an opportunity. According to Canary Media, the looming electricity
 AI And Hollywood's Next Golden AgeApr 29, 2025 am 11:09 AM
AI And Hollywood's Next Golden AgeApr 29, 2025 am 11:09 AMGenerative AI is revolutionizing film and television production. Luma's Ray 2 model, as well as Runway's Gen-4, OpenAI's Sora, Google's Veo and other new models, are improving the quality of generated videos at an unprecedented speed. These models can easily create complex special effects and realistic scenes, even short video clips and camera-perceived motion effects have been achieved. While the manipulation and consistency of these tools still need to be improved, the speed of progress is amazing. Generative video is becoming an independent medium. Some models are good at animation production, while others are good at live-action images. It is worth noting that Adobe's Firefly and Moonvalley's Ma
 Is ChatGPT Slowly Becoming AI's Biggest Yes-Man?Apr 29, 2025 am 11:08 AM
Is ChatGPT Slowly Becoming AI's Biggest Yes-Man?Apr 29, 2025 am 11:08 AMChatGPT user experience declines: is it a model degradation or user expectations? Recently, a large number of ChatGPT paid users have complained about their performance degradation, which has attracted widespread attention. Users reported slower responses to models, shorter answers, lack of help, and even more hallucinations. Some users expressed dissatisfaction on social media, pointing out that ChatGPT has become “too flattering” and tends to verify user views rather than provide critical feedback. This not only affects the user experience, but also brings actual losses to corporate customers, such as reduced productivity and waste of computing resources. Evidence of performance degradation Many users have reported significant degradation in ChatGPT performance, especially in older models such as GPT-4 (which will soon be discontinued from service at the end of this month). this


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

Atom editor mac version download
The most popular open source editor

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.

SublimeText3 Linux new version
SublimeText3 Linux latest version





