 Technology peripherals
Technology peripherals AI
AI ICLR 2024 Oral | To deal with distribution shifts that change over time, the University of Western Ontario and others proposed a learning time series trajectory method
ICLR 2024 Oral | To deal with distribution shifts that change over time, the University of Western Ontario and others proposed a learning time series trajectory method
The AIxiv column is a column where this site publishes academic and technical content. In the past few years, the AIxiv column of this site has received more than 2,000 reports, covering top laboratories from major universities and companies around the world, effectively promoting academic exchanges and dissemination. If you have excellent work that you want to share, please feel free to contribute or contact us for reporting. Submission email: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com
##The author Zeng Qiulin graduated from Harbin Institute of Technology and received a master's degree from the National University of Singapore. Under the guidance of Professor Wang Bo and Academician Ling Xiaofeng, during his doctoral period, he mainly carried out theoretical demonstration, method and application research on the distribution of random time changes. Currently, he has published many academic papers in ICLR/AAAI/IEEE TNNLS.
Personal homepage: https://hardworkingpearl.github.io/
Distribution shifts over time in real-world machine learning applications is a common question. This situation is framed as time-varying domain generalization (EDG), where the goal is to enable the model to generalize well to unseen target domains in time-varying systems by learning underlying evolving patterns across domains and exploiting these patterns. However, due to the limited number of timestamps in the EDG dataset, existing methods encounter challenges in capturing the evolving dynamics and avoiding overfitting to sparse timestamps, which limits their generalization and adaptability to new tasks. To solve this problem, we propose a new method SDE-EDG, which collects the infinite subdivision grid evolution trajectory (IFGET) of the data distribution through continuous interpolation samples to overcome the problem of overfitting. . Furthermore, by exploiting the inherent ability of stochastic differential equations (SDEs) to capture continuous trajectories, we propose to align the trajectories modeled by SDEs with those of IFGET through maximum likelihood estimation, thereby achieving the capture of distribution evolution trends.
- Paper title: Latent Trajectory Learning for Limited Timestamps under Distribution Shift over Time
- Paper link: https://openreview.net/pdf?id=bTMMNT7IdW
- Project link: https://github.com/HardworkingPearl/SDE-EDG-iclr2024
Method
Core Idea
To overcome this challenge, SDE-EDG proposes a novel approach by Construct an Infinitely Fined-Grid Evolving Trajectory (IFGET) to create consecutive interpolated samples in the latent representation space to bridge the gap between timestamps. In addition, SDE-EDG utilizes the inherent ability of Stochastic Differential Equations (SDEs) to capture continuous trajectory dynamics, and aligns the SDE modeled trajectories with IFGET through the path alignment regularizer to achieve cross-domain capture of evolving distribution trends. .Method details
1. Construct IFGET:First, SDE-EDG builds a sample-to-sample representation for each sample in the latent representation space. Correspondence, collect the evolution trajectory of each individual sample. For any sample of each category k at time  , we search for the
, we search for the  closest to it in the feature space at time
closest to it in the feature space at time  for its corresponding sample in
for its corresponding sample in  :
: 

Here  is to calculate the distance between two vectors,
is to calculate the distance between two vectors,  is the set of
is the set of  samples sampled from the next field
samples sampled from the next field  .
.
This correspondence is then used to generate continuous interpolation samples, aiming to connect the time gaps between timestamp intervals and avoid overfitting of sparse timestamps,

Here is sampled from the Beta distribution. By collecting the timing trace
is sampled from the Beta distribution. By collecting the timing trace of the samples generated in the above way, we get IFGET.
of the samples generated in the above way, we get IFGET.
2. Model trajectories using SDE:
SDE-EDG adopts neural SDE to model the continuous time trajectory of data in the latent space. Unlike traditional discrete timestamp-based models, SDE is naturally suitable for simulating continuous time trajectories. SDE-EDG models time series trajectories and can predict samples at any future time  through samples at time
through samples at time  :
:

Here the feature space variable  is It is predicted by the sample at time
is It is predicted by the sample at time  ,
,  is the drift function, and
is the drift function, and  is the diffusion function.
is the diffusion function.
3. Path alignment and maximum likelihood estimation:
SDE-EDG trains the model by maximizing the likelihood estimation of IFGET,

The final training function is  , and the first item is the error loss function for the prediction classification task.
, and the first item is the error loss function for the prediction classification task.
4. Experiment
下表展示了 SDE-EDG 与其他基线方法在多个数据集上分类准确率的比较。这些数据集包括 Rotated Gaussian (RG), Circle (Cir), Rotated MNIST (RM), Portraits (Por), Caltran (Cal), PowerSupply (PS), 和 Ocular Disease (OD)。结果显示,SDE-EDG 在所有数据集上的平均准确率均优于其他方法。

下图提供了一个直观的比较,展示了 SDE-EDG 算法(左)与传统 DG 方法 IRM(右)在特征表示方面的差异。通过数据特征空间的可视化,我们可以观察到 SDE-EDG 学习到的特征表示具有明显的决策边界,其中不同类别的数据点被清晰地区分开来,以不同形状表示,并且不同域的数据以彩虹条的颜色区分。这表明 SDE-EDG 能够成功捕捉数据随时间演变的动态,并在特征空间中保持类别的可分性。相比之下,IRM 的特征表示则倾向于将数据点坍缩到单一方向,导致决策边界不明显,这反映出 IRM 在捕捉时变分布趋势方面的不足。

下图通过一系列子图深入展示了 SDE-EDG 算法在捕捉数据随时间演变的能力方面的优势。子图 (a) 提供了 Sine 数据集的真实标签分布,其中正例和负例用不同颜色的点表示,为后续的比较提供了基准。接着,子图 (b) 和 (c) 分别展示了基于 ERM 的传统方法和 SDE-EDG 算法对同一数据集的预测结果,通过对比可以看出 SDE-EDG 在捕捉数据演变模式上的明显优势。子图 (d) 和 (e) 进一步揭示了 SDE-EDG 学习到的演变路径,其中 (d) 展示了应用了路径对齐损失(最大似然损失函数)后的路径,而 (e) 展示了未应用该损失时的路径。通过这一对比,可以直观地看到路径对齐损失对于确保模型能够正确捕捉和表征数据随时间变化的重要性。

-
下图子图 (a) 展示了在 Portraits 数据集上,使用不同算法进行训练时的准确率收敛轨迹。这个子图提供了一个直观的视角,用以比较 SDE-EDG 算法与其他基线方法(如 ERM、MLDG、GI)在训练过程中性能的变化情况。通过观察训练准确率随时间推移的增长趋势,我们可以评估不同算法的学习能力和收敛速度。SDE-EDG 算法的收敛轨迹尤其值得关注,因为它揭示了该算法在适应不断演变的数据分布时的效率和稳定性。
下图子图 (b) 和 (c) 分别展示了 RMNIST 和 Circle 数据集上,SDE-EDG 算法在这些数据集上的表现显示出其在处理时变分布时的优越性,即使在面对较大时间跨度的目标域时,也能保持较高的准确率,这表明了 SDE-EDG 算法在捕捉和适应数据演变模式方面的强大能力。
下图子图 (d) 和 (e) 探讨了最大似然损失(Maximum Likelihood Loss)在 RMNIST 和 PowerSupply 数据集上对 SDE-EDG 性能的影响。通过改变正则化权重 α 的值,这两个子图展示了不同 α 设置对模型性能的具体影响。实验结果表明,适当的 α 值可以显著提高 SDE-EDG 在特定数据集上的性能,这强调了在实际应用中根据数据集特性和任务需求调整超参数的重要性。

结论
论文作者提出了一种新的 SDE-EDG 方法,用于建模时变域泛化(EDG)问题。方法涉及通过识别样本到样本的对应关系并生成连续插值样本来构建 IFGET。随后,作者采用随机微分方程(SDE)并将其与 IFGET 对齐进行训练。文章的贡献在于揭示了通过收集个体的时间轨迹来捕获演变模式的重要性,以及在时间间隔之间进行插值以减轻源时间戳数量有限的问题,这有效地防止了 SDE-EDG 对有限时间戳的过拟合。
The above is the detailed content of ICLR 2024 Oral | To deal with distribution shifts that change over time, the University of Western Ontario and others proposed a learning time series trajectory method. For more information, please follow other related articles on the PHP Chinese website!
 The AI Skills Gap Is Slowing Down Supply ChainsApr 26, 2025 am 11:13 AM
The AI Skills Gap Is Slowing Down Supply ChainsApr 26, 2025 am 11:13 AMThe term "AI-ready workforce" is frequently used, but what does it truly mean in the supply chain industry? According to Abe Eshkenazi, CEO of the Association for Supply Chain Management (ASCM), it signifies professionals capable of critic
 How One Company Is Quietly Working To Transform AI ForeverApr 26, 2025 am 11:12 AM
How One Company Is Quietly Working To Transform AI ForeverApr 26, 2025 am 11:12 AMThe decentralized AI revolution is quietly gaining momentum. This Friday in Austin, Texas, the Bittensor Endgame Summit marks a pivotal moment, transitioning decentralized AI (DeAI) from theory to practical application. Unlike the glitzy commercial
 Nvidia Releases NeMo Microservices To Streamline AI Agent DevelopmentApr 26, 2025 am 11:11 AM
Nvidia Releases NeMo Microservices To Streamline AI Agent DevelopmentApr 26, 2025 am 11:11 AMEnterprise AI faces data integration challenges The application of enterprise AI faces a major challenge: building systems that can maintain accuracy and practicality by continuously learning business data. NeMo microservices solve this problem by creating what Nvidia describes as "data flywheel", allowing AI systems to remain relevant through continuous exposure to enterprise information and user interaction. This newly launched toolkit contains five key microservices: NeMo Customizer handles fine-tuning of large language models with higher training throughput. NeMo Evaluator provides simplified evaluation of AI models for custom benchmarks. NeMo Guardrails implements security controls to maintain compliance and appropriateness
 AI Paints A New Picture For The Future Of Art And DesignApr 26, 2025 am 11:10 AM
AI Paints A New Picture For The Future Of Art And DesignApr 26, 2025 am 11:10 AMAI: The Future of Art and Design Artificial intelligence (AI) is changing the field of art and design in unprecedented ways, and its impact is no longer limited to amateurs, but more profoundly affecting professionals. Artwork and design schemes generated by AI are rapidly replacing traditional material images and designers in many transactional design activities such as advertising, social media image generation and web design. However, professional artists and designers also find the practical value of AI. They use AI as an auxiliary tool to explore new aesthetic possibilities, blend different styles, and create novel visual effects. AI helps artists and designers automate repetitive tasks, propose different design elements and provide creative input. AI supports style transfer, which is to apply a style of image
 How Zoom Is Revolutionizing Work With Agentic AI: From Meetings To MilestonesApr 26, 2025 am 11:09 AM
How Zoom Is Revolutionizing Work With Agentic AI: From Meetings To MilestonesApr 26, 2025 am 11:09 AMZoom, initially known for its video conferencing platform, is leading a workplace revolution with its innovative use of agentic AI. A recent conversation with Zoom's CTO, XD Huang, revealed the company's ambitious vision. Defining Agentic AI Huang d
 The Existential Threat To UniversitiesApr 26, 2025 am 11:08 AM
The Existential Threat To UniversitiesApr 26, 2025 am 11:08 AMWill AI revolutionize education? This question is prompting serious reflection among educators and stakeholders. The integration of AI into education presents both opportunities and challenges. As Matthew Lynch of The Tech Edvocate notes, universit
 The Prototype: American Scientists Are Looking For Jobs AbroadApr 26, 2025 am 11:07 AM
The Prototype: American Scientists Are Looking For Jobs AbroadApr 26, 2025 am 11:07 AMThe development of scientific research and technology in the United States may face challenges, perhaps due to budget cuts. According to Nature, the number of American scientists applying for overseas jobs increased by 32% from January to March 2025 compared with the same period in 2024. A previous poll showed that 75% of the researchers surveyed were considering searching for jobs in Europe and Canada. Hundreds of NIH and NSF grants have been terminated in the past few months, with NIH’s new grants down by about $2.3 billion this year, a drop of nearly one-third. The leaked budget proposal shows that the Trump administration is considering sharply cutting budgets for scientific institutions, with a possible reduction of up to 50%. The turmoil in the field of basic research has also affected one of the major advantages of the United States: attracting overseas talents. 35
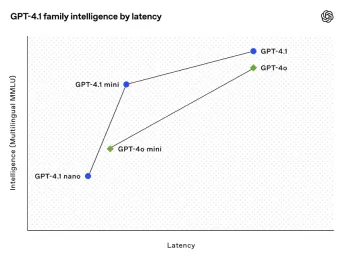 All About Open AI's Latest GPT 4.1 Family - Analytics VidhyaApr 26, 2025 am 10:19 AM
All About Open AI's Latest GPT 4.1 Family - Analytics VidhyaApr 26, 2025 am 10:19 AMOpenAI unveils the powerful GPT-4.1 series: a family of three advanced language models designed for real-world applications. This significant leap forward offers faster response times, enhanced comprehension, and drastically reduced costs compared t


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool

SublimeText3 Chinese version
Chinese version, very easy to use

Notepad++7.3.1
Easy-to-use and free code editor





