 Technology peripherals
Technology peripherals AI
AI Is Flash Attention stable? Meta and Harvard found that their model weight deviations fluctuated by orders of magnitude
Is Flash Attention stable? Meta and Harvard found that their model weight deviations fluctuated by orders of magnitudeIs Flash Attention stable? Meta and Harvard found that their model weight deviations fluctuated by orders of magnitude
Meta FAIR joins Harvard to provide a new research framework on data biases generated when optimizing large-scale machine learning.
As we all know, the training of large language models often takes months and uses hundreds or even thousands of GPUs. Taking the LLaMA2 70B model as an example, its training requires a total of 1,720,320 GPU hours. Training large models presents unique systemic challenges due to the scale and complexity of these workloads.
Recently, many institutions have reported instability during the training process when training SOTA generative AI models. They usually appear in the form of loss spikes, such as Google’s PaLM model training process There were as many as 20 loss spikes.
Numerical deviation is the root cause of this kind of training inaccuracy. Due to the extremely high execution cost of large language model training, how to quantify numerical deviation has become a key issue.
In a recent work, researchers from Meta and Harvard University developed a principled quantitative method to understand numerical bias in training optimization. To evaluate different state-of-the-art optimization techniques and determine whether they might introduce unexpected instabilities when used to train large models. The researchers found that although existing optimization methods performed well on some tasks, some numerical deviations occurred when applied to large models. This numerical bias may create instability during the training process, resulting in degraded model performance. In order to solve this problem, researchers proposed an optimization based on principled quantitative methods

- paper Title: Is Flash Attention Stable?
- Paper link: https://arxiv.org/pdf/2405.02803
It was found that during a single forward pass, the numerical deviation of Flash Attention An order of magnitude larger than the Baseline Attention of BF16.
Specifically, the method consists of two stages, including:
- Develop a micro-benchmark to perturb a given optimization Numerical accuracy;
- Evaluate how numerical deviations translate into changes in model weights through data-driven analysis based on Wasserstein distance.
The researchers analyzed the SOTA optimization technology Flash Attention and quantified the numerical deviation that may be introduced. Flash Attention is a technology widely used to accelerate attention mechanisms and is often considered a system bottleneck in the Transformer model. While Flash Attention improves speed and reduces memory access, it also relies on algorithm optimization, and algorithm optimization may lead to an increase in numerical deviation.
The researchers hypothesized that adding rescaling factors may introduce unintentional approximations, leading to numerical trade-offs, which may subsequently affect training stability.
They analyzed Flash Attention in the context of multimodal text-to-image workloads to determine the potential importance of numerical deviations between Flash Attention and its baseline. Ultimately, they introduce a framework to quantify the numerical bias of training optimization and its downstream effects.
The researchers have made the following two contributions in quantifying numerical deviations:
(1) Designed a micro-benchmark to separate numerical values Effect of precision on numerical bias.
The micro-benchmark designed by the researchers is a technique for measuring and quantifying the numerical deviations caused by traditional black-box optimization (such as Flash Attention). By perturbing aspects typically unavailable in the provided kernels, they pioneered the discovery that at low numerical precision (BF16), Flash Attention has approximately an order of magnitude higher numerical bias compared to Baseline Attention.
(2) Data-driven analysis based on Wasserstein Distance metric.
This analysis allows researchers to contextualize observed numerical deviations and form an upper bound on their impact on downstream model properties. In the researchers' case study, they were able to limit the impact of the observed numerical bias and found: "Flash Attention introduced model weight bias approximately 1/2 to 1/5 times that of low-precision training."
This study highlights the importance of developing a principled approach: "not only to quantify, but also to contextualize the impact of training optimization on numerical bias." By building proxies to Numerical bias is placed in context and is intended to infer the likelihood of downstream model effects (i.e., training instabilities) that are often difficult to measure.
Experimental Method
The researchers first developed a micro-benchmark to isolate and study the numerical deviation caused by Flash Attention. As shown in Figure 2, they numerically reimplemented Flash Attention to analyze different numerical precisions and apply potential optimization measures at each step of the algorithm.

#Figure 2: Microbenchmark design summary.
This is necessary because the Flash Attention kernel currently only supports FP16 and BF16 numeric formats. This kernel is also a wrapper API call for CUDA code, which makes it challenging to perturb the algorithm to examine the impact of numerical bias.
In contrast, their microbenchmark design allows precision input and modification within the algorithm. The researchers verified the microbenchmark against the original Flash Attention kernel.
They further designed a technique to compare the output of the Attention matrix at each step during model execution. And modified the model code to calculate Baseline Attention and Flash Attention every time attention is called, which allows accurate output matrix comparison for the same input matrix.
To put this into context, we also used the Max difference and Wasserstein Distance metrics to quantify the difference in model weights throughout training, using identical and independent training runs.
For training experiments, the researchers used a generative AI workload (i.e., text-to-image model) that converts text input into images. They retrained the model using the Shutterstock dataset and ran the experiment on a cluster of NVIDIA 80GB A100 GPUs.
Quantifying numerical deviations through micro-benchmarks
The researchers first analyzed the impact of Flash Attention in the forward pass process. They used microbenchmarks to examine the impact of different numerical precisions on the output matrix calculated by Attention, under the condition that the randomly initialized query, key, and value vectors were the same.
As shown in Figure 3, when researchers use different numerical formats ranging from BF16 to FP64, the numerical deviation between Flash Attention and Baseline Attention increases with the number of mantissa digits. And decrease. This suggests that the numerical difference is due to the approximation inherent in having fewer mantissa digits.

#Figure 3: The effect of numerical format on the numerical deviation of Flash Attention.
After that, the researcher set a "golden value" for Baseline Attention in the FP64 numerical format for standard comparison, and then compared the Attention output in different numerical formats with this value (such as shown in Figure 4).

Figure 4: Comparison of Baseline Attention "gold value" under FP64.
The results show that the numerical deviation of Flash Attention is about 10 times that of Baseline under BF16.
To further analyze this observed numerical deviation, the researchers scanned the sequence length of the matrix while keeping the tile size and SRAM size constant (as shown in Figure 5).

#Figure 5: Effect of sequence length on Flash Attention numerical deviation.
As shown in the figure, as the sequence length increases, whether it is measured by (a) the upper limit of the maximum difference, or by (b) the mean and standard deviation of the difference, Flash Attention The numerical deviations between both and Baseline Attention are increasing.
In addition, researchers also use micro-benchmark designs to conduct experiments with different optimizations to better understand the impact of numerical deviations (as shown in Figure 6).
Figure 6a shows how swapping the order of block dimensions results in an increased numerical difference between Flash Attention and Baseline Attention. Other perturbations in Figure 6b, such as limiting the tile size to squares, have no effect on the numerical bias. Figure 6c shows that the larger the block/tile size, the smaller the numerical deviation.

#Figure 6: Algorithm changes and their impact on observed numerical deviations.
Understand the numerical deviation through weight differences
Although Flash Attention may cause numerical deviation in Attention output during the forward pass, this The ultimate goal of the study is to determine if this has any impact during model training to investigate whether it can lead to instability in training.
Therefore, the researchers hope to quantify whether Flash Attention changes the model during training, that is, whether the difference in Attention output observed above is reflected in the updated model weights during training.
The researchers used two indicators to measure the difference in model weights between models trained using Baseline Attention and models trained using Flash Attention. First calculate the maximum difference, that is, find the absolute value of the difference between the weight matrices and take the maximum value, thereby obtaining the upper limit of the deviation, as follows:

Although the maximum difference provides an upper limit on the numerical deviation, it does not take into account the distribution of each matrix. Therefore, researchers quantify weight differences through Wasserstein Distance, which is a common measure of similarity between tensors. Although slightly more computationally complex, Wasserstein Distance includes shape information of the tensor distribution to measure similarity. The calculation formula is summarized as follows:

The lower the value, the higher the similarity between matrices.
Using these two indicators, the researchers then quantified how the model weights of Flash Attention changed compared to Baseline Attention throughout the training process:

According to the two indicators Wasserstein Distance and Max Difference, the addition of Flash Attention does change the model weight during the entire training process, and as the training continues, this This difference only gets bigger, indicating that a model trained with Flash Attention converges to a different model than the same model trained with Baseline Attention.
However, training is a stochastic process, and changes in certain model structures may produce similar results in terms of downstream effects and accuracy. This is noteworthy even if the weights of the models trained with Flash Attention and Baseline Attention are different.
Fully training a model and evaluating accuracy is a costly and resource-intensive task, especially for large models that take months to train.
The researcher configured a proxy to explore:
(a) How significant are these weight changes?
(b) Can this be related to standard weight changes in other widely adopted training optimizations?
In order to achieve this goal, the researchers designed a series of experiments to compare how the weight difference changes during the training process in different scenarios.
In addition to comparing the training process using Flash Attention and Baseline Attention, they also quantified the difference in weights during the same training process where the weights were initialized to different random values at the beginning of training. This provides a bound, as random weight initialization is a common technique and often produces equivalent results.
In addition, the researchers also measured changes in the weights of models trained with different accuracies. Numerical precision (i.e., FP16 vs. FP32) has the potential to cause downstream changes, which serves as an upper bound on the importance of Flash Attention weights.
As shown in Figure 8, it can be found that the model weight bias change rate using Flash Attention is equivalent to or smaller than the weight bias change rate of different model initializations (note the red and blue curves The slope of).
In addition, the weight change rate when using FP16 and FP32 is higher and the change is larger than when different models are initialized.
These results provide a proxy and show that: "While Flash Attention can exhibit numerical bias, it is limited by random model initialization and low-precision training. And the introduced model The weight deviation is approximately 1/2 to 1/5 times that of low-precision training."

For more research details, please refer to the original paper.
The above is the detailed content of Is Flash Attention stable? Meta and Harvard found that their model weight deviations fluctuated by orders of magnitude. For more information, please follow other related articles on the PHP Chinese website!
 The AI Skills Gap Is Slowing Down Supply ChainsApr 26, 2025 am 11:13 AM
The AI Skills Gap Is Slowing Down Supply ChainsApr 26, 2025 am 11:13 AMThe term "AI-ready workforce" is frequently used, but what does it truly mean in the supply chain industry? According to Abe Eshkenazi, CEO of the Association for Supply Chain Management (ASCM), it signifies professionals capable of critic
 How One Company Is Quietly Working To Transform AI ForeverApr 26, 2025 am 11:12 AM
How One Company Is Quietly Working To Transform AI ForeverApr 26, 2025 am 11:12 AMThe decentralized AI revolution is quietly gaining momentum. This Friday in Austin, Texas, the Bittensor Endgame Summit marks a pivotal moment, transitioning decentralized AI (DeAI) from theory to practical application. Unlike the glitzy commercial
 Nvidia Releases NeMo Microservices To Streamline AI Agent DevelopmentApr 26, 2025 am 11:11 AM
Nvidia Releases NeMo Microservices To Streamline AI Agent DevelopmentApr 26, 2025 am 11:11 AMEnterprise AI faces data integration challenges The application of enterprise AI faces a major challenge: building systems that can maintain accuracy and practicality by continuously learning business data. NeMo microservices solve this problem by creating what Nvidia describes as "data flywheel", allowing AI systems to remain relevant through continuous exposure to enterprise information and user interaction. This newly launched toolkit contains five key microservices: NeMo Customizer handles fine-tuning of large language models with higher training throughput. NeMo Evaluator provides simplified evaluation of AI models for custom benchmarks. NeMo Guardrails implements security controls to maintain compliance and appropriateness
 AI Paints A New Picture For The Future Of Art And DesignApr 26, 2025 am 11:10 AM
AI Paints A New Picture For The Future Of Art And DesignApr 26, 2025 am 11:10 AMAI: The Future of Art and Design Artificial intelligence (AI) is changing the field of art and design in unprecedented ways, and its impact is no longer limited to amateurs, but more profoundly affecting professionals. Artwork and design schemes generated by AI are rapidly replacing traditional material images and designers in many transactional design activities such as advertising, social media image generation and web design. However, professional artists and designers also find the practical value of AI. They use AI as an auxiliary tool to explore new aesthetic possibilities, blend different styles, and create novel visual effects. AI helps artists and designers automate repetitive tasks, propose different design elements and provide creative input. AI supports style transfer, which is to apply a style of image
 How Zoom Is Revolutionizing Work With Agentic AI: From Meetings To MilestonesApr 26, 2025 am 11:09 AM
How Zoom Is Revolutionizing Work With Agentic AI: From Meetings To MilestonesApr 26, 2025 am 11:09 AMZoom, initially known for its video conferencing platform, is leading a workplace revolution with its innovative use of agentic AI. A recent conversation with Zoom's CTO, XD Huang, revealed the company's ambitious vision. Defining Agentic AI Huang d
 The Existential Threat To UniversitiesApr 26, 2025 am 11:08 AM
The Existential Threat To UniversitiesApr 26, 2025 am 11:08 AMWill AI revolutionize education? This question is prompting serious reflection among educators and stakeholders. The integration of AI into education presents both opportunities and challenges. As Matthew Lynch of The Tech Edvocate notes, universit
 The Prototype: American Scientists Are Looking For Jobs AbroadApr 26, 2025 am 11:07 AM
The Prototype: American Scientists Are Looking For Jobs AbroadApr 26, 2025 am 11:07 AMThe development of scientific research and technology in the United States may face challenges, perhaps due to budget cuts. According to Nature, the number of American scientists applying for overseas jobs increased by 32% from January to March 2025 compared with the same period in 2024. A previous poll showed that 75% of the researchers surveyed were considering searching for jobs in Europe and Canada. Hundreds of NIH and NSF grants have been terminated in the past few months, with NIH’s new grants down by about $2.3 billion this year, a drop of nearly one-third. The leaked budget proposal shows that the Trump administration is considering sharply cutting budgets for scientific institutions, with a possible reduction of up to 50%. The turmoil in the field of basic research has also affected one of the major advantages of the United States: attracting overseas talents. 35
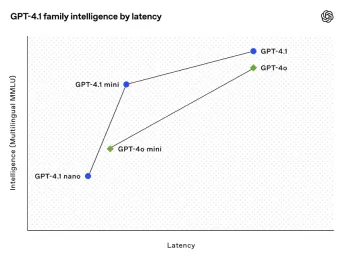 All About Open AI's Latest GPT 4.1 Family - Analytics VidhyaApr 26, 2025 am 10:19 AM
All About Open AI's Latest GPT 4.1 Family - Analytics VidhyaApr 26, 2025 am 10:19 AMOpenAI unveils the powerful GPT-4.1 series: a family of three advanced language models designed for real-world applications. This significant leap forward offers faster response times, enhanced comprehension, and drastically reduced costs compared t


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

WebStorm Mac version
Useful JavaScript development tools

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

SublimeText3 English version
Recommended: Win version, supports code prompts!






