Specific implementation of non-recursive algorithm for binary tree pre-order traversal_javascript skills

In the previous article, we talked about the recursive traversal algorithm of binary trees (Improvement of root-first (pre-order) traversal of binary trees). This article mainly talks about the non-recursive algorithm of binary trees, using stack structure

The non-recursive algorithm idea obtained by root traversal is summarized as follows:

1) Push into the stack, mainly push the head node into the stack first, and then visit this node

2) while, loop through the current node until there is no node in the left child

3) If the right child of the node is true, go to 1) and continue traversing, otherwise exit the current node and go to the parent node and go to 1)

Let’s first look at the algorithm that conforms to this idea:

Copy code The code is as follows:

int PreOrderTraverseNonRecursiveEx(const BiTree &T, int (*VisitNode) (TElemType data))
{
if (T == NULL)
{
return -1;
}

BiTNode *pBiNode = T;
SqStack S;
InitStack(&S);
Push(&S, (SElemType)T);

while (!IsStackEmpty(S))
{
while (pBiNode)
{
VisitNode(pBiNode->data);
if (pBiNode != T)
{
Push(&S, (SElemType)pBiNode);
}                                > Pop(&S, (SElemType*)&pBiNode);
}
if (pBiNode->rchild == NULL)
{
Pop(&S, (SElemType*)&pBiNode); // If the stack is empty at this time, there is a problem
}
pBiNode = pBiNode->rchild;
}

return 0;
}

Note: 1) The stack structure is used here, please refer to the above
Stack stored in sequential structure

2) When saving the node here, I save the pointer, which is the address of the node, and change it to int type storage. When popping, the pointer is used, so &pBiNode is taken, and It's not pBiNode. Why please think about the use of pointers by yourself. The best understanding is BiTNode *pBiNode; it is easy to understand if the definition is changed to BiTree pBiNode.

The above algorithm is actually wrong! Why? I checked here for a long time, and during this period, infinite loops occurred, and the right subtree did not display after exiting from the left subtree. Finally, I modified the first while judgment condition. Why? Because if after pop, the stack is empty but the right subtree is still there, we can't continue. I didn't do much verification after I wrote it. I will explain it later. There is no null pointer pushed here. Let's take a look at the push. An example of a null pointer is mainly pushed onto the stack when the left subtree is empty, as follows:

Copy code

The code is as follows:int PreOrderTraverseNonRecursive(const BiTree &T, int (*VisitNode) (TElemType data)){ if (T == NULL)

{

return -1;
}

BiTNode *pBiNode = T;
SqStack S;
InitStack(&S);
Push(&S, (SElemType)T);

while (!IsStackEmpty(S))
{
GetTop(S, (SElemType*)&pBiNode);
while (pBiNode)

{

VisitNode(pBiNode->data );
pBiNode = pBiNode->lchild;
Push (&S, (SElemType)pBiNode); , (SElemType*)&pBiNode);
}
if ( !IsStackEmpty(S))
{
Pop(&S, (SElemType*)&pBiNode);
pBiNode = pBiNode-> rchild;
Push(&S, (SElemType)pBiNode);
}
}

return 0;
}

This is like this, first push the root node, and then determine whether the left subtree is empty. If it is not empty, push it onto the stack. Otherwise, after exiting the while loop, pop the NULL node out of the stack, and then determine whether the current stack is Empty, if it is not empty, pop the stack to get the parent node, then determine the right child, push the right child node, and then determine whether the left child of the right subtree is empty, and continue the loop.

There are two wasteful places here: one is to push empty child nodes onto the stack, and the other is to frequently use GetTop to obtain the top element of the stack

Here we go back and look at the algorithm we originally designed. There happens to be no NULL pointer or empty child node pushed in, but the output is not complete. Here we think of adding it when judging the stack. Currently It is ok if the node is NULL, so that there will be no embarrassment that the left subtree node will not be displayed and the right subtree node cannot be displayed, as follows:

Copy code The code is as follows:

//Non-recursive pre-order traversal of the binary tree
int PreOrderTraverseNonRecursiveEx(const BiTree &T,
int (*VisitNode)(TElemType data))
{
if (T == NULL)
{
return -1;
}

BiTNode *pBiNode = T;
SqStack S;
InitStack(&S);
Push(&S, (SElemType)T);

while ( !IsStackEmpty(S) || pBiNode) //The main modification is this sentence
{
while (pBiNode)
{
VisitNode(pBiNode->data);
if (pBiNode != T)
{
Push(&S, (SElemType)pBiNode);
}
pBiNode = pBiNode->lchild;
}
if( pBiNode == NULL)
{
Pop(&S, (SElemType*)&pBiNode);
}
if ( pBiNode->rchild == NULL)
{
Pop( &S, (SElemType*)&pBiNode); //If the stack is empty at this time, there is a problem
}
pBiNode = pBiNode->rchild;
}
return 0;
}

After adding this to the first while loop, it is OK. The test case is similar to the binary tree pre-order traversal. Test the binary tree example in the previous section as follows:

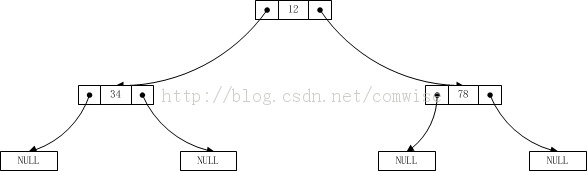
The input data at this time is still 12 34 0 0 78 0 0. The test results are as follows:

--- BiTree ---
Please Enter BiTree Node data:
12
Please Enter BiTree Node data:
34
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
78
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
12 34 78

This is not enough for testing, let’s look at the following binary tree

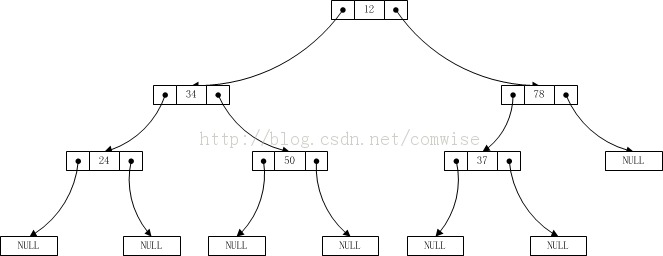
The input data at this time should be: 12 34 24 0 0 50 0 0 78 37 0 0 0. The test results are as follows:

--- BiTree ---
Please Enter BiTree Node data:
12
Please Enter BiTree Node data:
34
Please Enter BiTree Node data:
24
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
50
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
78
Please Enter BiTree Node data:
37
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
12 34 24 50 78 37

It can be seen from pre-order traversal that it is exactly correct. In addition, these algorithms are not only for pre-order traversal. If you want to change it to in-order or post-order, you only need to remove the visit and the like in the above algorithm, and then Add it to the appropriate location and you’re done