Umkehrung nach Explosion? KAN, der „in einer Nacht einen MLP getötet hat“: Eigentlich bin ich auch ein MLP

Multilayer Perceptron (MLP), auch bekannt als vollständig verbundenes Feedforward-Neuronales Netzwerk, ist der Grundbaustein der heutigen Deep-Learning-Modelle. Die Bedeutung von MLPs kann nicht genug betont werden, da sie die Standardmethode zur Approximation nichtlinearer Funktionen beim maschinellen Lernen sind.

Aber kürzlich haben Forscher des MIT und anderer Institutionen eine sehr vielversprechende alternative Methode vorgeschlagen – KAN. Diese Methode übertrifft MLP hinsichtlich Genauigkeit und Interpretierbarkeit. Darüber hinaus kann es MLPs übertreffen, die mit viel größeren Parametergrößen und sehr wenigen Parametern ausgeführt werden. Die Autoren gaben beispielsweise an, dass sie mit KAN die mathematischen Gesetze in der Knotentheorie wiederentdecken und die Ergebnisse von DeepMind mit kleineren Netzwerken und einem höheren Automatisierungsgrad reproduzieren konnten. Konkret verfügt DeepMinds MLP über etwa 300.000 Parameter, während KAN nur etwa 200 Parameter hat.

Der Feinabstimmungsinhalt lautet wie folgt: Diese erstaunlichen Forschungsergebnisse machten KAN schnell populär und lockten viele Menschen dazu, es zu studieren. Bald äußerten einige Leute Zweifel. Unter ihnen geriet ein Colab-Dokument mit dem Titel „KAN is just MLP“ in den Mittelpunkt der Diskussion.

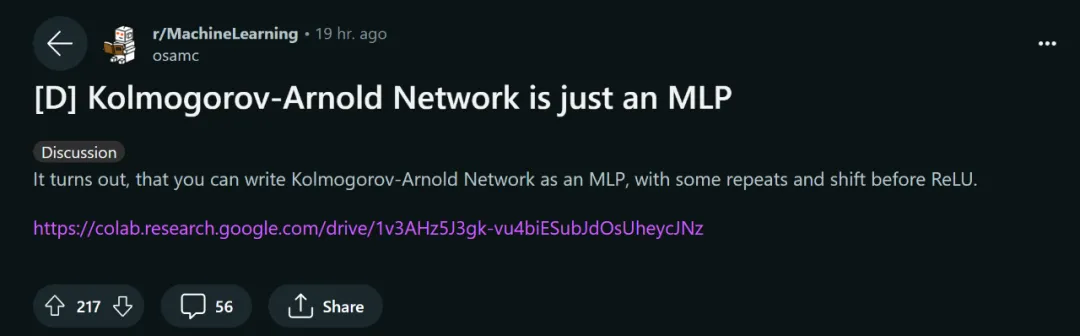
KAN Nur ein normaler MLP?

Der Autor des oben genannten Dokuments gab an, dass Sie KAN als MLP schreiben können, indem Sie vor ReLU einige Wiederholungen und Verschiebungen hinzufügen.

In einem kurzen Beispiel zeigt der Autor, wie man das KAN-Netzwerk in ein gewöhnliches MLP mit der gleichen Anzahl an Parametern und einer leicht nichtlinearen Struktur umschreibt.

Was man bedenken muss, ist, dass KAN an den Rändern Aktivierungsfunktionen hat. Sie verwenden B-Splines. In den gezeigten Beispielen verwenden die Autoren der Einfachheit halber nur stückweise lineare Funktionen. Die Modellierungsfähigkeiten des Netzwerks werden dadurch nicht verändert.

Hier ist ein Beispiel für eine stückweise lineare Funktion:

def f(x):if x 

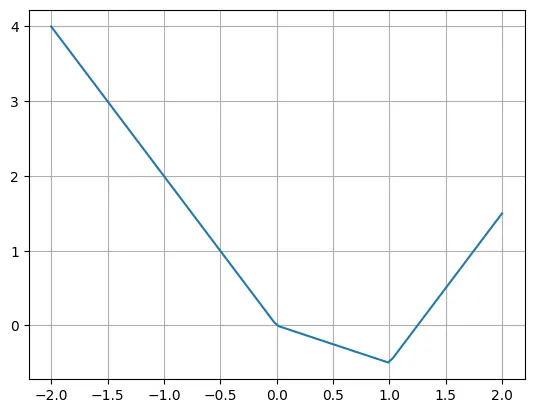
Der Autor gab an, dass wir diese Funktion mithilfe mehrerer ReLU- und linearer Funktionen problemlos umschreiben können. Beachten Sie, dass es manchmal notwendig ist, die Eingabe von ReLU zu verschieben.

plt.plot(X, -2*X + torch.relu(X)*1.5 + torch.relu(X-1)*2.5)plt.grid()

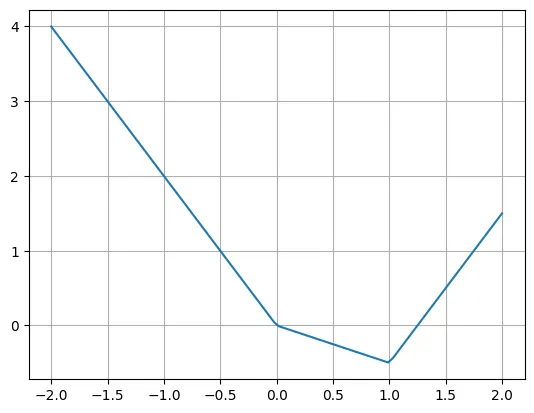
Die eigentliche Frage ist, wie man die KAN-Schicht in eine typische MLP-Schicht umschreiben kann. Angenommen, es gibt n Eingabeneuronen und m Ausgabeneuronen und die stückweise Funktion hat k Teile. Dies erfordert n*m*k Parameter (k Parameter pro Kante, und Sie haben n*m Kanten).

Betrachten Sie nun eine KAN-Kante. Dazu muss die Eingabe k-mal kopiert, jede Kopie um eine Konstante verschoben und dann durch ReLU und lineare Schichten (mit Ausnahme der ersten Schicht) ausgeführt werden. Grafisch sieht es so aus (C ist die Konstante und W ist das Gewicht):

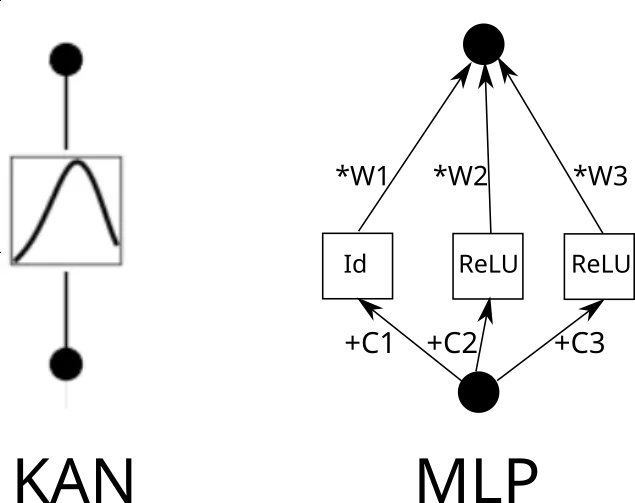
Jetzt können Sie diesen Vorgang für jede Kante wiederholen. Beachten Sie jedoch Folgendes: Wenn das Raster der stückweisen linearen Funktion überall gleich ist, können wir die ReLU-Zwischenausgabe teilen und einfach die Gewichte darauf mischen. So:

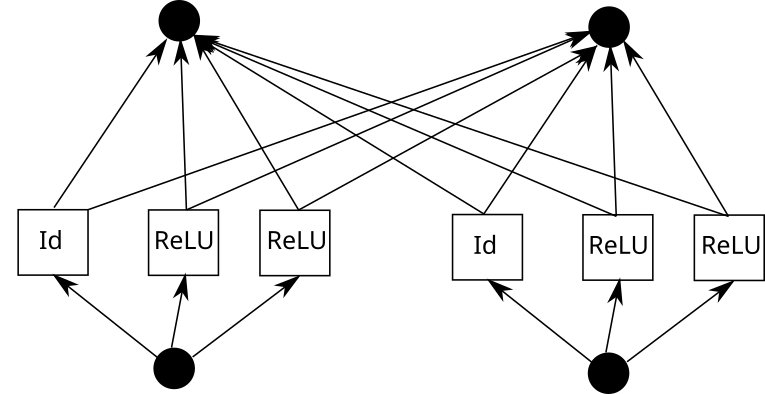
In Pytorch bedeutet dies:

k = 3 # Grid sizeinp_size = 5out_size = 7batch_size = 10X = torch.randn(batch_size, inp_size) # Our inputlinear = nn.Linear(inp_size*k, out_size)# Weightsrepeated = X.unsqueeze(1).repeat(1,k,1)shifts = torch.linspace(-1, 1, k).reshape(1,k,1)shifted = repeated + shiftsintermediate = torch.cat([shifted[:,:1,:], torch.relu(shifted[:,1:,:])], dim=1).flatten(1)outputs = linear(intermediate)

Jetzt sehen unsere Ebenen so aus:

• Erweitern + Umschalt + ReLU
• Linear

Betrachten Sie die drei Ebenen nacheinander:

• Erweitern + Umschalt +. ReLU (Schicht 1 beginnt hier)
• Linear
• Erweitern + Umschalt + ReLU (Ebene 2 beginnt hier)
• Linear
• Erweitern + Umschalt + ReLU (Ebene 3 beginnt hier Hier beginnen)
• Linear

Obwohl wir die Eingabeerweiterung ignorieren, können wir Folgendes neu anordnen:

• Linear (Ebene 1 beginnt hier)
• Erweitern + Umschalt + ReLU
• Linear (Ebene 2 beginnt hier)
• Erweitern + Umschalt + ReLU

Die folgende Ebene kann grundsätzlich als MLP bezeichnet werden. Sie können die lineare Ebene auch vergrößern und die Erweiterung und Verschiebung entfernen, um bessere Modellierungsmöglichkeiten zu erhalten (allerdings mit einem höheren Parameteraufwand).

• Linear (Schicht 2 beginnt hier)
• Expand + Shift + ReLU

Anhand dieses Beispiels zeigt der Autor, dass KAN eine Art MLP ist. Diese Aussage veranlasste alle, die beiden Arten von Methoden zu überdenken.

Überprüfung der Ideen, Methoden und Ergebnisse von KAN

Tatsächlich wurde KAN neben der unklaren Beziehung zu MLP auch durch viele andere Aspekte in Frage gestellt.

Zusammenfassend konzentrierte sich die Diskussion der Forscher hauptsächlich auf die folgenden Punkte.

Erstens liegt der Hauptbeitrag von KAN in der Interpretierbarkeit, nicht in der Erweiterungsgeschwindigkeit, Genauigkeit usw.

Der Autor des Artikels sagte einmal:

1. KAN skaliert schneller als MLP. KAN hat eine bessere Genauigkeit als MLP mit weniger Parametern.
2. KAN kann intuitiv visualisiert werden. KAN bietet Interpretierbarkeit und Interaktivität, die MLP nicht bieten kann. Mithilfe von KANs können wir möglicherweise neue wissenschaftliche Gesetze entdecken.

Unter ihnen ist die Bedeutung der Interpretierbarkeit des Netzwerks für das Modell zur Lösung realer Probleme offensichtlich:

Aber das Problem ist: „Ich denke, ihr Anspruch ist genau das.“ Es lernt schneller und ist interpretierbar. Ersteres macht Sinn, wenn KAN viel weniger Parameter hat als das entsprechende NN. Was genau kann KAN also? weniger Parameter als das entsprechende NN?

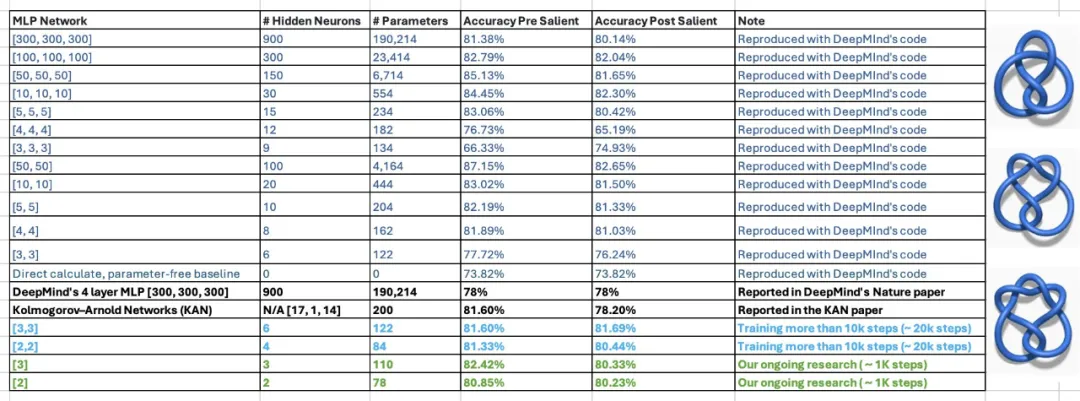
Diese Aussage ist immer noch fragwürdig. In dem Artikel gaben die Autoren von KAN an, dass sie DeepMinds Forschung zu mathematischen Theoremen mit einem MLP von 300.000 Parametern und nur 200 Parametern von KAN reproduzieren konnten. Nachdem sie die Ergebnisse gesehen hatten, untersuchten zwei Studenten des außerordentlichen Professors Humphrey Shi von der Georgia Tech die Experimente von DeepMind erneut und stellten fest, dass DeepMinds MLP mit nur 122 Parametern die Genauigkeit von KAN von 81,6 % erreichen konnte. Darüber hinaus haben sie keine wesentlichen Änderungen am DeepMind-Code vorgenommen. Um dieses Ergebnis zu erzielen, reduzierten sie lediglich die Netzwerkgröße, verwendeten zufällige Seeds und erhöhten die Trainingszeit.

Als Antwort gab der Autor des Papiers ebenfalls eine positive Antwort:

Zweitens unterscheiden sich KAN und MLP nicht grundlegend in der Methode.

„Ja, das ist offensichtlich dasselbe. In KAN machen sie zuerst die Aktivierung und dann die lineare Kombination, während sie in MLP zuerst die lineare Kombination und dann die Aktivierung machen. Verstärken, im Grunde ist das dasselbe.“ Soweit ich weiß, sind die Hauptgründe für die Verwendung von KAN Interpretierbarkeit und symbolische Regression. „Neben der Infragestellung der Methode forderten die Forscher auch die Rückgabe der Bewertung dieser Arbeit. Begründung:

„Ich denke, Leute.“ Wir müssen aufhören, das KAN-Papier als grundlegende Veränderung in der Grundeinheit des Deep Learning zu betrachten, sondern es einfach als ein gutes Papier zur Interpretierbarkeit von Deep Learning betrachten. Lernen auf allen Ebenen Die Interpretierbarkeit nichtlinearer Funktionen ist der Hauptbeitrag dieses Papiers . „

Drittens sagten einige Forscher, dass die Idee von KAN nicht neu sei.

„Die Leute haben sich in den 1980er-Jahren damit befasst. In einer Hacker-News-Diskussion wurde eine italienische Zeitung erwähnt, in der dieses Problem diskutiert wurde. Das ist also überhaupt nichts Neues. 40 Jahre später ist dies einfach etwas, das entweder zurückkam oder abgelehnt wurde.“ und wurde erneut aufgegriffen.

„Diese Ideen sind nicht neu, aber ich glaube nicht, dass der Autor davor zurückschreckt. Er hat einfach alles gut verpackt und einige schöne Experimente zu Spielzeugdaten durchgeführt.“

Gleichzeitig wurde auch der Aufsatz MaxOut (https://arxiv.org/pdf/1302.4389) von Ian Goodfellow und Yoshua Bengio vor mehr als zehn Jahren erwähnt Die Ideen sind einigermaßen ähnlich.

Autor: Das ursprüngliche Forschungsziel war tatsächlich Interpretierbarkeit

Als Ergebnis der hitzigen Diskussion meldete sich einer der Autoren, Sachin Vaidya.

Als einer der Autoren dieses Papiers möchte ich ein paar Worte sagen. Die Aufmerksamkeit, die KAN erhält, ist erstaunlich, und diese Diskussion ist genau das, was wir brauchen, um neue Technologien an ihre Grenzen zu bringen und herauszufinden, was funktioniert und was nicht.

Ich dachte, ich würde einige Hintergrundinformationen zum Thema Motivation mitteilen. Unsere Hauptidee zur Implementierung von KAN resultiert aus unserer Suche nach interpretierbaren KI-Modellen, die die Erkenntnisse der Physiker über Naturgesetze „lernen“ können. Daher konzentrieren wir uns, wie andere erkannt haben, ausschließlich auf dieses Ziel, da herkömmliche Black-Box-Modelle keine Erkenntnisse liefern können, die für grundlegende Entdeckungen in der Wissenschaft von entscheidender Bedeutung sind. Anschließend zeigen wir anhand von Beispielen aus Physik und Mathematik, dass KAN traditionelle Methoden hinsichtlich der Interpretierbarkeit deutlich übertrifft. Wir hoffen auf jeden Fall, dass der Nutzen von KAN weit über unsere ursprünglichen Beweggründe hinausgeht.

Auf der GitHub-Homepage antwortete auch Liu Ziming, einer der Autoren des Papiers, auf die Auswertung dieser Forschung:

Die häufigste Frage, die mir in letzter Zeit gestellt wurde, ist, ob KAN die nächste Generation werden wird LLM. Ich habe dazu kein klares Urteil.

KAN wurde für Anwendungen entwickelt, die Wert auf hohe Genauigkeit und Interpretierbarkeit legen. Die Interpretierbarkeit von LLMs liegt uns zwar am Herzen, aber Interpretierbarkeit kann für LLMs und die Wissenschaft sehr unterschiedliche Bedeutungen haben. Ist uns eine hohe Genauigkeit des LLM wichtig? Die Skalierungsgesetze scheinen dies zu implizieren, aber vielleicht nicht sehr genau. Darüber hinaus kann Genauigkeit für LLM und Wissenschaft auch unterschiedliche Bedeutungen haben.

Ich begrüße Menschen, die KAN kritisieren. Übung ist das einzige Kriterium, um die Wahrheit zu prüfen. Es gibt viele Dinge, die wir im Voraus nicht wissen, bis sie tatsächlich ausprobiert werden und sich als Erfolg oder Misserfolg erweisen. Obwohl ich KAN gerne erfolgreich sehen würde, bin ich ebenso neugierig auf das Scheitern von KAN.

KAN und MLP ersetzen einander nicht. Sie haben jeweils in einigen Fällen Vorteile und in einigen Fällen Einschränkungen. Ich wäre an theoretischen Rahmenwerken interessiert, die beides umfassen und vielleicht sogar neue Alternativen hervorbringen (Physiker lieben einheitliche Theorien, sorry).

KAN Der Erstautor des Artikels ist Liu Ziming. Er ist Physiker und Forscher im Bereich maschinelles Lernen und ist derzeit Doktorand im dritten Jahr am MIT und IAIFI bei Max Tegmark. Seine Forschungsinteressen konzentrieren sich auf die Schnittstelle zwischen künstlicher Intelligenz und Physik.

Das obige ist der detaillierte Inhalt vonUmkehrung nach Explosion? KAN, der „in einer Nacht einen MLP getötet hat“: Eigentlich bin ich auch ein MLP. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!