Heim >Technologie-Peripheriegeräte >KI >Eine Staffel über mehr als 300 Jahre: Inspiriert von Terence Teru beschlossen Mathematiker, KI zu nutzen, um den Beweis von Fermats letztem Satz zu formalisieren.
Eine Staffel über mehr als 300 Jahre: Inspiriert von Terence Teru beschlossen Mathematiker, KI zu nutzen, um den Beweis von Fermats letztem Satz zu formalisieren.
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2024-05-03 13:04:01885Durchsuche
Inspiriert von Terence Tao beginnen immer mehr Mathematiker, künstliche Intelligenz für die mathematische Erforschung zu nutzen. Diesmal geht es um Fermats letzten Satz, eines der zehn schwierigsten mathematischen Probleme der Welt. Der letzte Satz von Fermat ist ein sehr komplexes mathematisches Problem, für das bisher keine praktikable Lösung gefunden wurde. Mathematiker hoffen, dass sie mit der leistungsstarken Rechenleistung und den intelligenten Algorithmen der künstlichen Intelligenz in der Mathematik forschen können

Der letzte Satz von Fermat, auch bekannt als „Fermats letzter Satz (FLT)“, wurde im 17. Jahrhundert von Franzosen vorgeschlagen Mathematiker Pierre de Fermat. Dahinter steckt eine sagenumwobene Geschichte. Es heißt, dass Fermat um 1637, als er die lateinische Übersetzung der Arithmetik des Diophantus las, neben Proposition 8 von Band 11 schrieb: „Dividiere eine Kubikzahl durch die Summe von zwei Kubikzahlen, oder es ist unmöglich, eine vierte zu dividieren.“ Potenz in die Summe von zwei vierten Potenzen, oder allgemein eine Potenz höher als die zweite Potenz in die Summe von zwei Potenzen derselben Potenz „Ich bin überzeugt, dass ich etwas darüber herausgefunden habe. Das ist eine wunderbare Demonstration, aber leider Der Leerraum hier ist zu klein, um ihn aufzuschreiben. „

Was in diesem Absatz angegeben wird, ist der Inhalt von Fermats letztem Satz: Wenn die ganze Zahl n>2 ist, hat die Gleichung über x^n + y^n=z^n keine positive ganzzahlige Lösung.
Fei Ma sagte, er wisse, wie man es beweist, aber er habe es nicht geschrieben, weil die Lücke im Buch zu klein sei. Später gab es Kontroversen über die Echtheit der Geschichte und ob Fermat die Beweismethode wirklich herausgefunden hatte Seit mehr als 300 Jahren arbeiten Mathematiker hart daran, Fermats letzten Satz zu beweisen. Erst 1995 hat Professor Andrew Wiles von der Princeton University in den USA den Beweis fertiggestellt
Nachdem der letzte Satz von Fermat bewiesen wurde, was können Mathematiker sonst noch mit KI tun? Die Antwort lautet: Formalisierung in der Mathematik bezieht sich normalerweise darauf und Mengenlehre), um mathematische Objekte, Strukturen, Theoreme und Beweise so auszudrücken, dass sie auf Computern dargestellt, überprüft und bearbeitet werden können, wodurch die Genauigkeit und Konsistenz mathematischer Inhalte sichergestellt wird. Die Entwicklung der Mathematik lässt sich bis ins späte 19. Jahrhundert zurückverfolgen Anfang des 20. Jahrhunderts, während die moderne formale Mathematik mit der Entwicklung der mathematischen Logik und Informatik im 20. Jahrhundert begann.
Das Hauptziel der formalen Mathematik besteht darin, ein formales System zu etablieren, das eine Reihe von Symbolen, eine Reihe grundlegender Axiome und eine Reihe von Argumentationsregeln umfasst. Durch die Verwendung dieser Regeln und Axiome ist es möglich, 
In einem Blog stellte er die Hintergründe, Motivation und konkreten Methoden hierfür vor.
Warum den Beweis von Fermats letztem Satz formalisieren?
Historisch gesehen waren mehrere andere große Durchbrüche in der algebraischen Zahlentheorie (wie die Theorie der Faktorisierung in Zahlenkörpern und die Arithmetik in zyklischen Körpern) zumindest teilweise durch den Wunsch nach einem tieferen Verständnis der FLT motiviert.
Wiles' Arbeit, ergänzt durch seinen Schüler Richard Taylor, baute auf einem umfassenden Fundament der Mathematik des 20. Jahrhunderts auf. Die von Wiles eingeführte Grundtechnik – das „Modularity-Lifting-Theorem“ – wurde in den 30 Jahren seit der Veröffentlichung des Originalpapiers konzeptionell stark vereinfacht und weitgehend verallgemeinert. Dieses Feld ist auch heute noch sehr aktiv. Frank Calegaris Beitrag auf dem Internationalen Mathematikerkongress 2022, in dem die Fortschritte seit Wiles‘ Durchbruch dargelegt werden (siehe: https://arxiv.org/abs/2109.14145). Kevin Buzzard sagte, dass die fortgesetzte Aktivität auf diesem Gebiet einer seiner Beweggründe für die Formalisierung des FLT-Beweises sei.
Formalisierung der Mathematik, die Kunst, Mathematik auf dem Papier in eine Computerprogrammiersprache umzuwandeln, die in der Lage ist, Theoreme zu verstehen und Konzepte zu beweisen. Diese Programmiersprachen, auch als interaktive Theorembeweiser (ITPs) bekannt, gibt es schon seit Jahrzehnten. In den letzten Jahren scheint dieser Bereich jedoch einige Aufmerksamkeit in der mathematischen Gemeinschaft auf sich gezogen zu haben. Wir haben mehrere Beispiele für die Formalisierung der Forschung in der Mathematik gesehen, das jüngste davon ist die Formalisierung des Beweises der polynomischen Freiman-Ruzsa-Vermutung durch Terence Tao und andere. Dieses bahnbrechende Papier aus dem Jahr 2023 wurde in nur drei Wochen in Lean formalisiert. Solche Erfolgsgeschichten könnten den Betrachter zu der Annahme verleiten, dass ITPs wie Lean nun bereit sind, die gesamte moderne Mathematik zu formalisieren.
Allerdings ist die Wahrheit alles andere als so einfach. In einigen Bereichen der Mathematik, beispielsweise der Kombinatorik, können wir beobachten, wie einige moderne Durchbrüche in Echtzeit formalisiert werden. Buzzard sagte jedoch, er habe regelmäßig Londoner Seminare zur Zahlentheorie besucht und dabei oft bemerkt, dass Leans Kenntnisse moderner mathematischer Definitionen nicht ausreichten, um die auf den Seminaren angekündigten Ergebnisse zu formulieren, geschweige denn ihre Beweise zu überprüfen.
Tatsächlich war die „Verzögerung“ in diesem Aspekt der Zahlentheorie eine der Hauptmotivationen von Buzzard, mit der Formalisierung des zeitgenössischen Beweises von FLT zu beginnen. Am Ende des Projekts wird Lean in der Lage sein, automorphe Formen (eine spezielle Klasse von Funktionen komplexer Variablen) und Darstellungen, Galois-Darstellungen, latenten Automorphismus, Modularitätsförderungssätze, Arithmetik algebraischer Varietäten, Klassenkörpertheorie und arithmetische Duale-Theoreme zu verstehen , Shimura-Varietäten und andere Konzepte, die in der modernen algebraischen Zahlentheorie verwendet werden. Nach Ansicht von Buzzard wird es angesichts dieser Grundlagen keine Science-Fiction mehr sein, die Ereignisse in seinem eigenen Fachgebiet zu formalisieren.
Also, warum machst du das? Buzzard erklärt: „Wenn wir einigen Informatikern glauben, wird das exponentielle Wachstum der künstlichen Intelligenz es Computern schließlich ermöglichen, Mathematiker bei ihrer Forschung zu unterstützen. Solche Arbeiten können Computern helfen, zu verstehen, was wir in der modernen mathematischen Forschung tun.“ das Projekt?
Das Formalisierungsprojekt von Fermats letztem Satz wurde jetzt gestartet. Buzzard zeigt den aktuellen Fortschritt in einer Grafik an.
Interessierte Forscher können die Details lesen: https://imperialcollegelondon.github.io/FLT/blueprint/dep_graph_document.html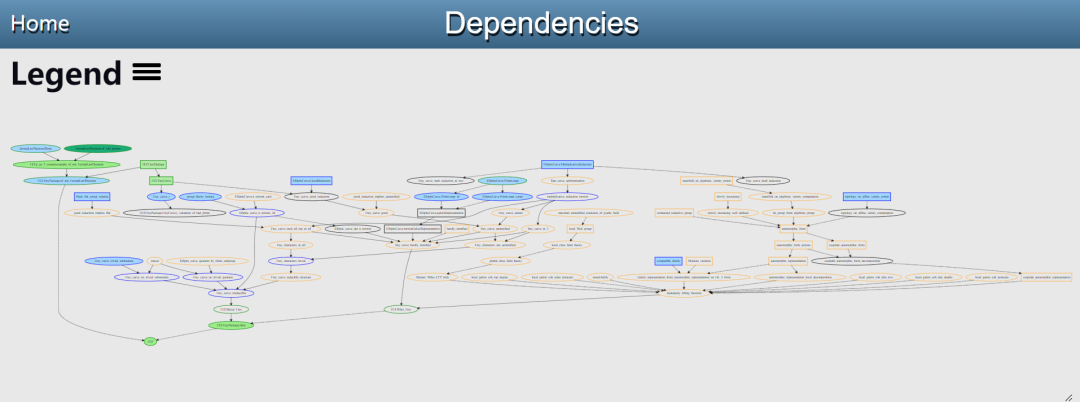
Link zum Lehrbuch: https://leanprover-community.github.io/mathematics_in_lean/
Lean Zulip-Chat-Link: https://leanprover.zulipchat.com/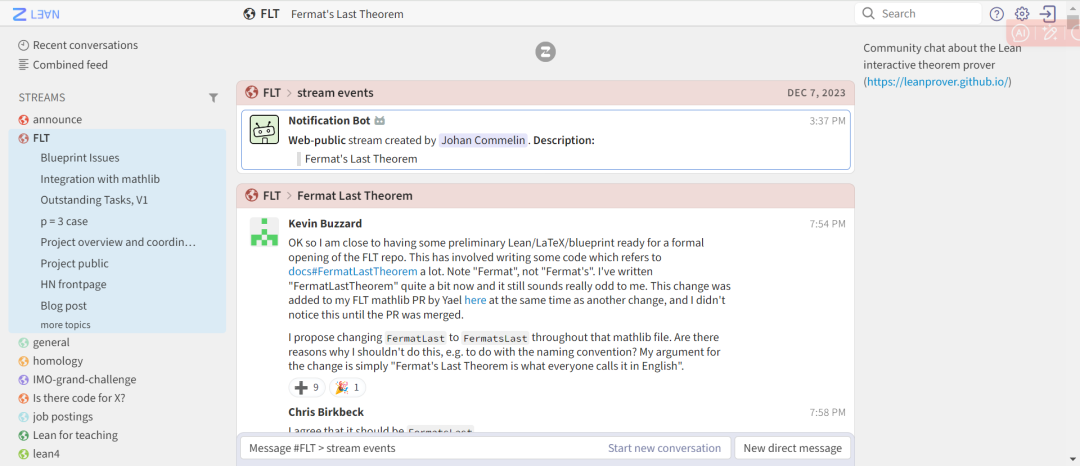
Gleichzeitig werden auch formale Proof-Tools wie Lean ständig iteriert. Im Vergleich zum ursprünglichen Lean verfügt die neueste Lean 4-Version über zahlreiche Optimierungen, darunter einen schnelleren Compiler, eine verbesserte Fehlerbehandlung und eine bessere Integration mit externen Tools.
Ende letzten Jahres haben das Team der offenen Plattform LeanDojo und Forscher von Caltech außerdem Lean Copilot auf den Markt gebracht, ein Kollaborationstool, das für die Interaktion großer Sprachmodelle mit Menschen entwickelt wurde und die Leistungsfähigkeit großer KI-Modelle in die mathematische Forschung einbringt.
„Ich gehe davon aus, dass KI bei richtiger Anwendung bis 2026 zu einem vertrauenswürdigen Co-Autor in der mathematischen Forschung und vielen anderen Bereichen werden wird“, sagte Terence Tao in einem früheren Blog.
Ich hoffe, dass Terence Taos Vorhersage bald wahr wird.
Verwandte Lektüre:
《Tao Zhexuans neues Projekt: Beweis des Primzahlsatzes in Lean, der Forschungsentwurf ist fertig》
Referenzlink: https://leanprover.zulipchat.com/#narrow/ Stream /416277-FLT
Das obige ist der detaillierte Inhalt vonEine Staffel über mehr als 300 Jahre: Inspiriert von Terence Teru beschlossen Mathematiker, KI zu nutzen, um den Beweis von Fermats letztem Satz zu formalisieren.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

