Beim Minimum-Cut-Problem ungerichteter Graphen wurde ein neuer Durchbruch erzielt, und die Google-Forschung gewann den SODA 2024 Best Paper Award

Der Google-Blog hat neue Forschungsergebnisse veröffentlicht, um das Minimum-Cut-Problem ungerichteter Graphen zu lösen.

1996 schlugen der amerikanische Informatiker David R. Karger und andere Forscher in der Arbeit „Ein neuer Ansatz für das Minimum-Cut-Problem“ einen überraschenden randomisierten Algorithmus vor, der in der theoretischen Informatik sehr beliebt ist Sehr wichtig, besonders geeignet für ungefähre Minimalschnittprobleme in großräumigen Diagrammen.

Kargers Algorithmus kann einen minimalen Schnittpunkt in einem Diagramm in der Zeit O (m log^3n) finden, die sie als nahezu lineare Zeit bezeichnen, was lineare Multiplikation mit einem polylogarithmischen Faktor bedeutet.

In einem gerade von Google aktualisierten Blog stellten sie einen zuvor veröffentlichten Artikel „Deterministic Near-Linear Time Minimum Cut in Weighted Graphs“ vor und die Forschung gewann den ACM-SIAM SODA24 Best Paper Award. Der Artikel beschreibt einen neuen Algorithmus, der in nahezu linearer Zeit ausgeführt wird (statt nahezu linearer Zeit). Dieser Algorithmus ist deterministisch und kann den korrekten Mindestschnitt zuverlässig finden. Er verbessert den vorherigen Algorithmus, dessen Korrektheit oder Anwendbarkeit nicht garantiert werden kann zu Algorithmen für einfache Graphen. Dies ist wohl die größte Entdeckung seit Kargers berühmtem Randomisierungsalgorithmus.

• Papieradresse: https://arxiv.org/pdf/2401.05627.pdf
• Papiertitel: Deterministic Near-Linear Time Minimum Cut in Weighted Graphs

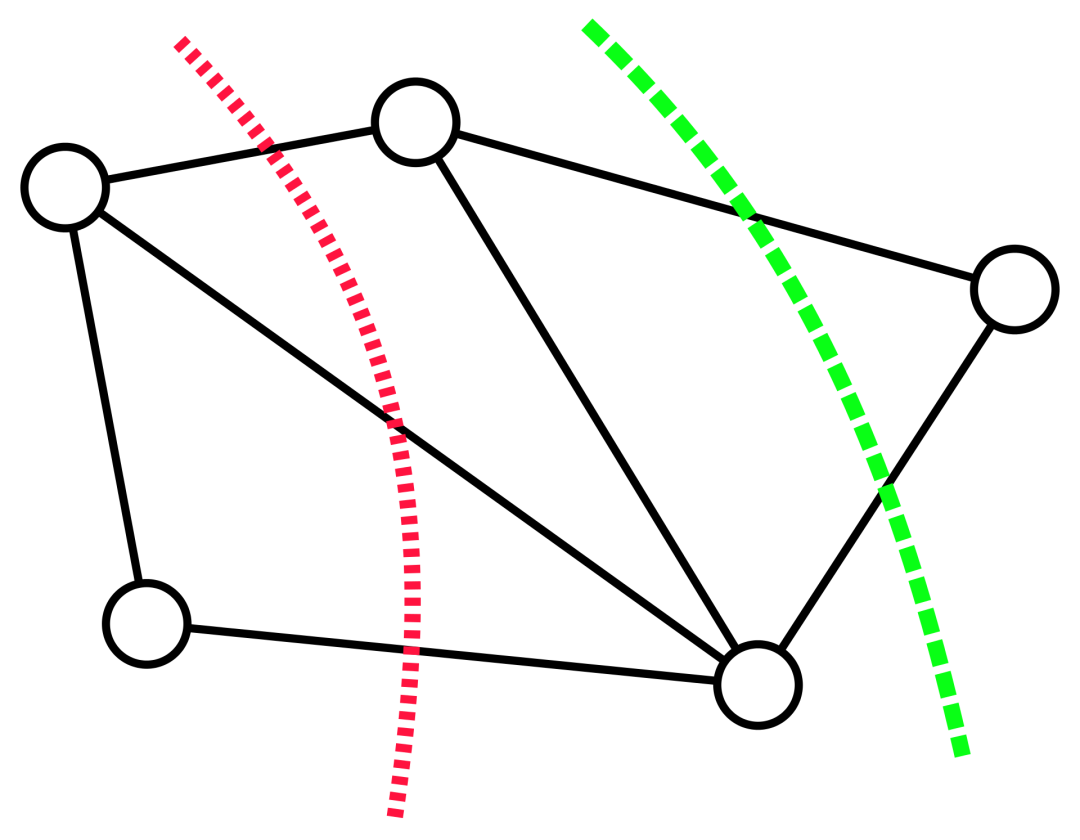
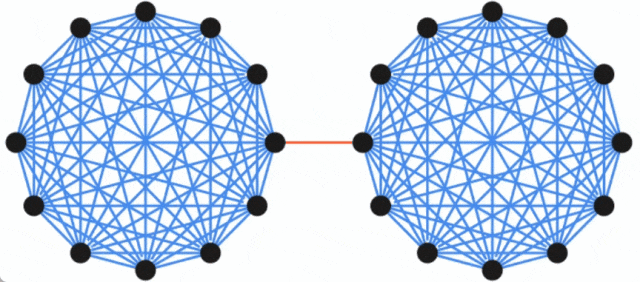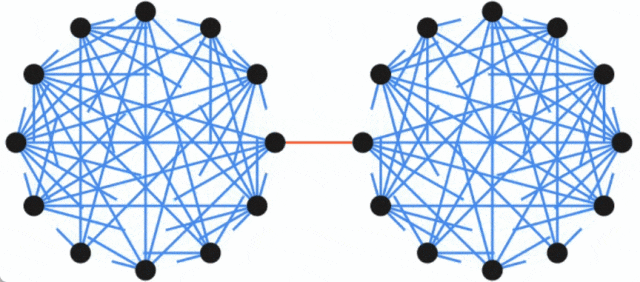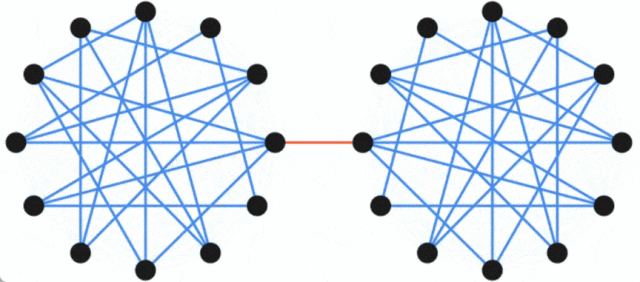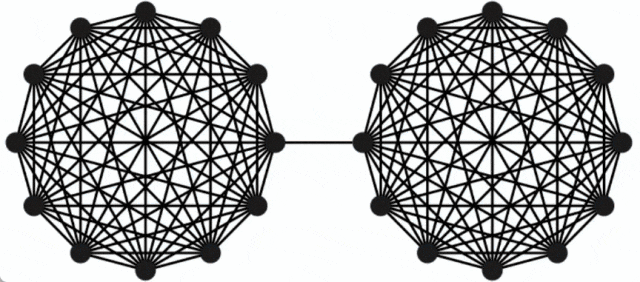
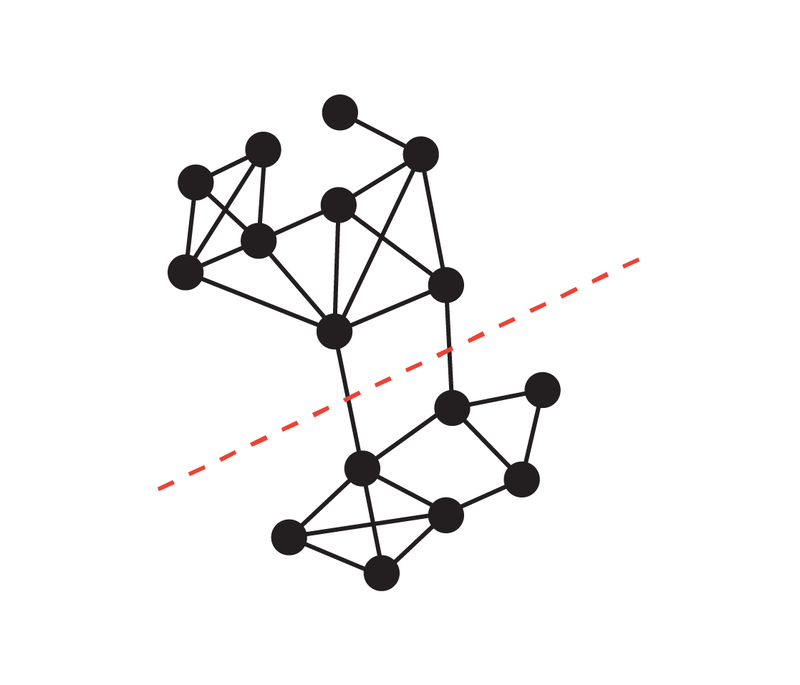
Hinweis: am kleinsten Das Cut-Problem (oft als Minimum Cut bezeichnet) ist ein grundlegendes strukturelles Problem der Graphkonnektivität. Es konzentriert sich im Allgemeinen auf die einfachste Möglichkeit, das Netzwerk zu trennen. In der Graphentheorie wird die Menge von Kanten, die durch Entfernen aller Kanten dazu führen kann, dass ein Netzwerkflussdiagramm nicht mehr verbunden (d. h. in zwei Untergraphen unterteilt) ist, als Schnitt des Diagramms bezeichnet, und der kleinste Schnitt in einem Diagramm wird als a bezeichnet minimaler Schnitt.

                                                                                                                                                                        ^{Ein Diagramm und seine zwei Schnitte: Die rot gepunktete Linie markiert einen Schnitt mit drei Kanten und die grüne gestrichelte Linie stellt einen minimalen Schnitt (einschließlich zwei Kanten) dieses Diagramms dar.}

Einführung in die Methode

In Bezug auf das Minimum-Cut-Problem entwickelte Karger 1996 einen nahezu linearen Zeit-Zufallsalgorithmus, der den Minimum-Cut mit hoher Wahrscheinlichkeit finden kann, und die Arbeit liefert auch Ergebnisse Eine wichtige Erkenntnis ist, dass es ein kleineres Diagramm gibt, das die Größe aller Schnitte weitgehend beibehält.

Diese Entdeckung ist nützlich, da langsamere Algorithmen mit kleineren Diagrammen als Eingabe ausgeführt werden können und die langsamere Laufzeit (in Bezug auf die Größe des kleineren Diagramms) immer noch mit der Originalgröße (größer) vergleichbar ist Die Grafik ist nahezu linear.

Tatsächlich werden viele strukturelle Entdeckungen zum Minimalschnittproblem in diese Richtung durchgeführt.

Google führt dies aus, indem es von einem Graphen G mit n Knoten ausgeht und dann auf der schnitterhaltenden Sparseness-Methode basiert, die im Artikel „Randomized Approximation Schemes for Cuts and Flows in Capacitated Graphs“ (verfasst von Benzur, Karger) vorgeschlagen wird ) beweist, dass ein dünn besetzter Graph G' mit weniger Kanten konstruiert werden kann, und in diesem Graphen ist die Größe fast aller Schnitte ungefähr gleich der Größe der entsprechenden Schnitte im ursprünglichen Graphen G.

Dieses Konzept lässt sich anhand des folgenden Beispiels veranschaulichen: Der ursprüngliche Graph besteht aus zwei vollständigen Graphen, die durch eine einzelne Kante verbunden sind, während der spärliche Graph weniger Kanten hat, aber die Kantengewichte größer sind und alle Schnitte Die Größe beträgt grob erhalten.

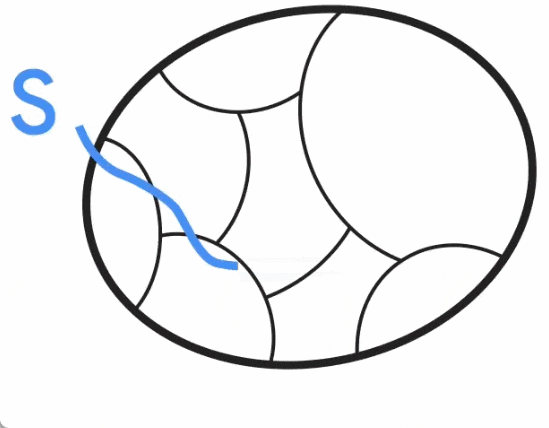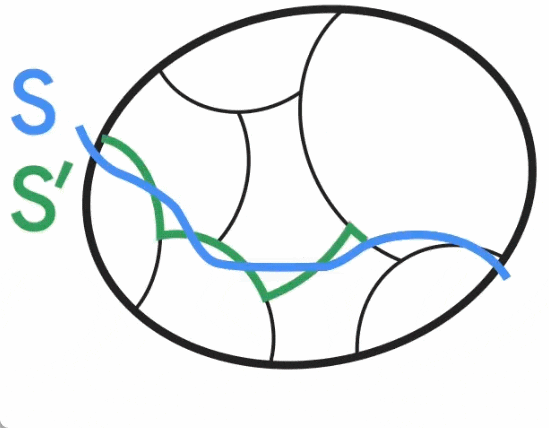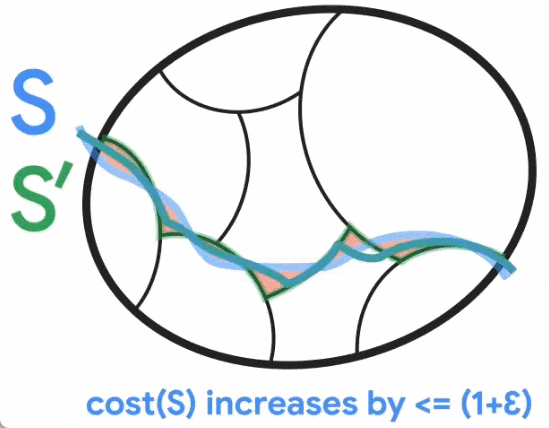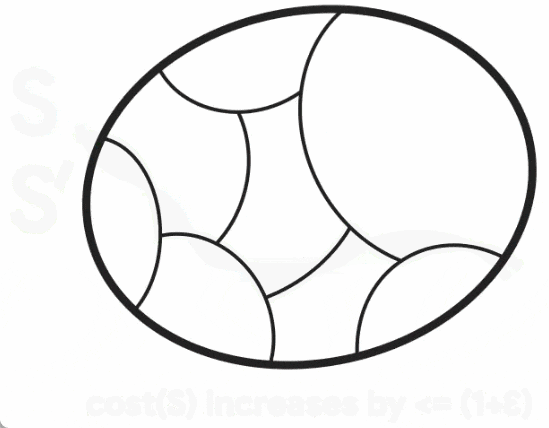
Um diesen dünner besiedelten Graphen zu erstellen, haben Benzur und Karger die Methode der unabhängigen Kantenabtastung übernommen. Bei dieser Methode besteht für jede Kante im Diagramm G eine bestimmte Wahrscheinlichkeit, dass sie im Diagramm G' enthalten ist, und ihr Gewicht in G' wird entsprechend dem Kehrwert der Stichprobenwahrscheinlichkeit verstärkt (z. B. wenn das ursprüngliche Gewicht einer Kante beträgt). 1 Die Kante wird mit einer Wahrscheinlichkeit von 10 % einbezogen, dann wird ihr Gewicht auf 10 angepasst. Es stellt sich heraus, dass dieser sehr einfache (nahezu lineare Zeit-)Ansatz mit hoher Erfolgswahrscheinlichkeit schnitterhaltende Graphsparsifikationen konstruieren kann.

Der Karger-Algorithmus ist jedoch ein Monte-Carlo-Algorithmus, d. h. die Ausgabe kann mit einer geringen Wahrscheinlichkeit falsch sein, und es gibt keine bekannte Möglichkeit, festzustellen, ob die Ausgabe korrekt ist, außer sie mit einem tatsächlich bekannten Mindestschnitt zu vergleichen .

Daher haben Forscher hart daran gearbeitet, Wege zur Lösung des offenen Problems nahezu linearer zeitdeterministischer Algorithmen zu finden. Da die Konstruktion der schnitterhaltenden Graphsparsifizierung die einzige stochastische Komponente des Karger-Algorithmus ist, besteht ein Ansatz darin, eine deterministische Konstruktion der Sparsifizierung in nahezu linearer Zeit zu finden (auch Derandomisierung genannt).

Im Jahr 2015 erreichten Kawarabayashi und Thorup einen wichtigen Meilenstein – sie fanden einen deterministischen nahezu linearen Zeitalgorithmus für einfache Graphen (d. h. Graphen mit höchstens einer Kante zwischen jedem Knotenpaar und allen Kantengewichten gleich 1).

Die Studie führt zu einer Schlüsselidee, nämlich dass es einige Zusammenhänge zwischen minimalen Schnitten und einer anderen wichtigen Graphenstruktur (sogenannter „Schnitt mit niedriger Leitfähigkeit“) gibt. Diese Verbindung war entscheidend für die spätere Derandomisierung des Karger-Algorithmus in allgemeinen kantengewichteten Diagrammen und half Google bei der Ableitung seines neuen Algorithmus.

Ausrichtung von minimalem Schnitt und Schnitt mit niedriger Leitfähigkeit

Die Leitfähigkeit des Diagrammschnitts S ist definiert als das Verhältnis der Schnittgröße von S zum Volumen von S (vorausgesetzt, dass S der ist). Seite des Schnitts mit kleinerem Volumen und ist nicht leer), wobei das Volumen von S der Grad der Knoten in S ist.

Die niedrige Leitfähigkeit des Schnitts S erfasst intuitiv den Engpass im Netzwerk, da nur eine kleine Anzahl von Kanten (im Verhältnis zu seinem Volumen) S mit dem Rest des Diagramms verbinden. Der Leitwert eines Diagramms ist als der minimale Leitwert für jeden Schnitt im Diagramm definiert, und Diagramme mit großem Leitwert (auch erweiterte Diagramme genannt) gelten als gut verbunden, da es im Inneren keine Engpässe gibt.

                                                                            ^.

Kawayabarashi und Thorup beobachteten, dass in einfachen Diagrammen mit großen minimalen Knotengraden jeder nichttriviale (d. h. mindestens zwei Knoten auf jeder Seite) minimale Schnitt eine niedrige Leitfähigkeit aufweisen muss. Basierend auf dieser Beobachtung muss die Partitionierung, wenn der Graph in gut verbundene Cluster unterteilt werden kann, mit jedem nichttrivialen Min-Schnitt konsistent sein, da jeder Cluster genau auf einer Seite jedes Schnitts liegen muss. Anschließend wird jeder Cluster auf einen Knoten verkleinert und ein kleinerer Graph verarbeitet, bei dem alle nicht trivialen Minimalschnitte des ursprünglichen Graphen intakt sind.

Für gewichtete Diagramme gilt die obige Beobachtung jedoch nicht mehr, und die gleiche Partitionierung, die im Fall des einfachen Diagramms verwendet wird, stimmt möglicherweise nicht genau mit nicht trivialen Mindestschnitten überein.

Wie in der Abbildung unten dargestellt, stellte Jason Li im Jahr 2021 fest, dass diese Aufteilung immer noch in etwa mit dem nicht trivialen Mindestschnitt übereinstimmt. Insbesondere für einen nicht trivialen minimalen Schnitt S gibt es einen Schnitt S', der S ähnlich ist, sodass S' mit dem Cluster konsistent ist. Jason Li stellte außerdem fest, dass diese Eigenschaft der Partitionierung ausgenutzt werden kann, um die Konstruktion der schnitterhaltenden Graphsparsität effektiv zu derandomisieren.

Der neue von Google entwickelte Algorithmus zielt darauf ab, eine Partition zu erstellen, um den Anwendungsfall von Min-Cut zu formulieren. Die Google-Studie ist präziser und schneller als die allgemeineren Standardmethoden, die Jason Li in früheren Arbeiten verwendet hat. Die neue Forschung optimiert die Laufzeit bei gleichzeitiger Gewährleistung der Genauigkeit und erreicht schließlich einen nahezu linearen zeitdeterministischen Algorithmus für das Minimalschnittproblem.

^{Referenzlink: https://research.google/blog/solving-the-minimum-cut-problem-for-undirected-graphs/}

Das obige ist der detaillierte Inhalt vonBeim Minimum-Cut-Problem ungerichteter Graphen wurde ein neuer Durchbruch erzielt, und die Google-Forschung gewann den SODA 2024 Best Paper Award. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!