Transparent! Eine ausführliche Analyse der Prinzipien der wichtigsten Modelle des maschinellen Lernens!

Laienhaft ausgedrückt ist ein Modell für maschinelles Lernen eine mathematische Funktion, die Eingabedaten einer vorhergesagten Ausgabe zuordnet. Genauer gesagt ist ein Modell für maschinelles Lernen eine mathematische Funktion, die Modellparameter anpasst, indem sie aus Trainingsdaten lernt, um den Fehler zwischen der vorhergesagten Ausgabe und der wahren Bezeichnung zu minimieren.

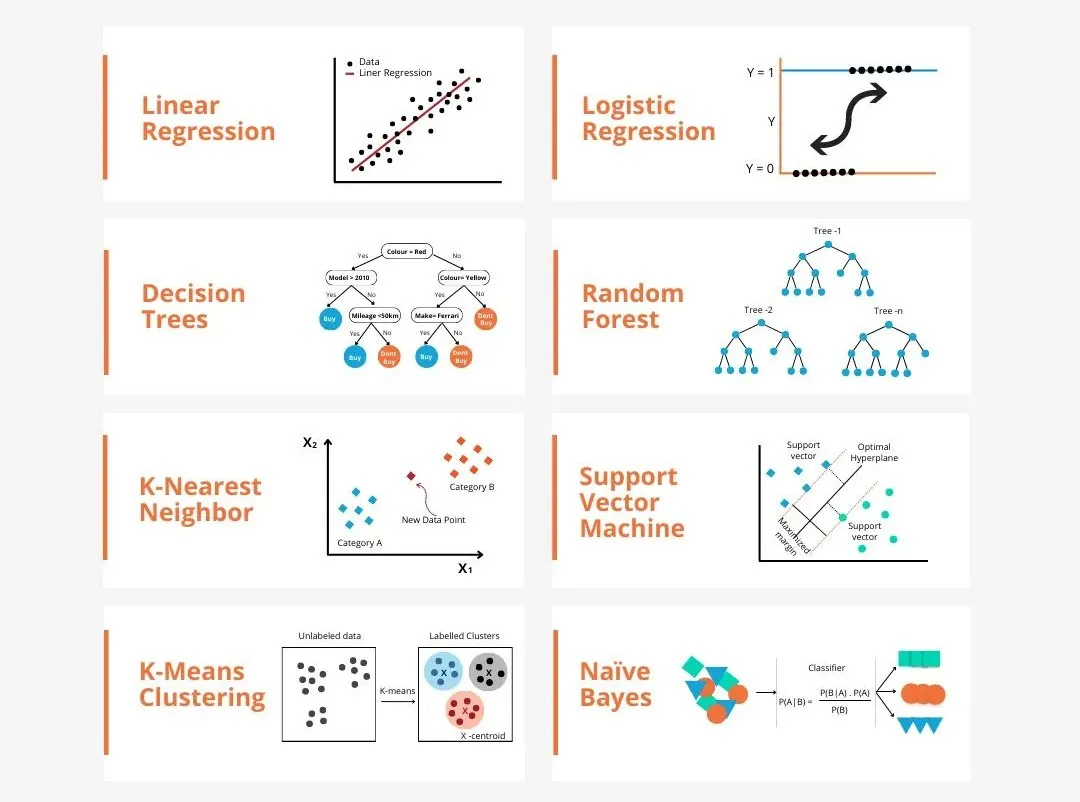
Es gibt viele Modelle im maschinellen Lernen, wie z. B. logistische Regressionsmodelle, Entscheidungsbaummodelle, Support-Vektor-Maschinenmodelle usw. Jedes Modell hat seinen anwendbaren Datentyp und Problemtyp. Gleichzeitig gibt es viele Gemeinsamkeiten zwischen verschiedenen Modellen oder es gibt einen verborgenen Weg für die Modellentwicklung.

Nehmen Sie das konnektionistische Perzeptron als Beispiel: Indem wir die Anzahl der verborgenen Schichten des Perzeptrons erhöhen, können wir es in ein tiefes neuronales Netzwerk umwandeln. Wenn dem Perzeptron eine Kernelfunktion hinzugefügt wird, kann es in eine SVM umgewandelt werden. Dieser Prozess kann intuitiv die intrinsischen Verbindungen zwischen verschiedenen Modellen sowie die möglichen Transformationen zwischen Modellen demonstrieren. Entsprechend der Ähnlichkeiten habe ich die Modelle grob (nicht streng) in die folgenden 6 Kategorien unterteilt, um die Entdeckung grundlegender Gemeinsamkeiten zu erleichtern und sie einzeln eingehend zu analysieren!

1. Modell des neuronalen Netzwerks (konnektionistisch):

Das konnektionistische Modell ist ein Computermodell, das die Struktur und Funktion des neuronalen Netzwerks des menschlichen Gehirns simuliert. Seine Grundeinheit ist ein Neuron. Jedes Neuron empfängt Eingaben von anderen Neuronen und verändert den Einfluss der Eingaben auf das Neuron, indem es das Gewicht anpasst. Das neuronale Netzwerk ist eine Black Box, die durch die Wirkung mehrerer nichtlinearer verborgener Schichten einen ähnlichen Effekt erzielen kann.

Repräsentative Modelle umfassen DNN, SVM, Transformer und LSTM. In einigen Fällen kann die letzte Schicht eines tiefen neuronalen Netzwerks als logistisches Regressionsmodell betrachtet werden, das zur Klassifizierung von Eingabedaten verwendet wird. Die Support-Vektor-Maschine kann auch als eine spezielle Art von neuronalem Netzwerk betrachtet werden. Sie besteht nur aus zwei Schichten: Die Eingabeschicht und die Ausgabeschicht implementieren zusätzlich komplexe nichtlineare Transformationen durch Kernelfunktionen, um ähnliche Effekte wie tiefe neuronale Netzwerke zu erzielen. Das Folgende ist eine Analyse des Prinzips des klassischen DNN-Modells:

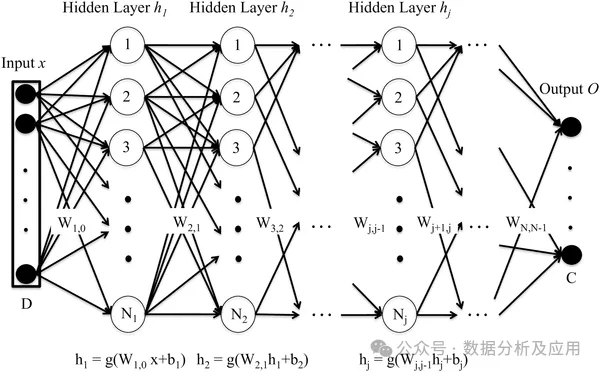
Das tiefe neuronale Netzwerk (DNN) besteht aus mehreren Neuronenschichten. Durch den Vorwärtsausbreitungsprozess werden die Eingabedaten an jede Neuronenschicht übertragen und Schicht für Schicht berechnet, um eine Ausgabe zu erhalten. Jede Neuronenschicht empfängt die Ausgabe der Neuronen der vorherigen Schicht als Eingabe und gibt sie an die Neuronen der nächsten Schicht aus. Der Trainingsprozess von DNN wird durch den Backpropagation-Algorithmus implementiert. Während des Trainingsprozesses wird der Fehler zwischen der Ausgabeschicht und der realen Bezeichnung berechnet, der Fehler wird an jede Schicht von Neuronen zurückpropagiert und die Gewichte und Bias-Terme der Neuronen werden gemäß dem Gradientenabstiegsalgorithmus aktualisiert. Durch die wiederholte Iteration dieses Prozesses werden die Netzwerkparameter kontinuierlich optimiert und der Vorhersagefehler des Netzwerks letztendlich minimiert.

Der Vorteil des tiefen neuronalen Netzwerks (DNN) ist seine leistungsstarke Fähigkeit zum Lernen von Funktionen. DNN kann die Eigenschaften von Daten automatisch lernen, ohne Features manuell entwerfen zu müssen. Hochgradig nichtlineare und starke Generalisierungsfähigkeit. Der Nachteil besteht darin, dass DNN eine große Anzahl von Parametern erfordert, was zu Überanpassungsproblemen führen kann. Gleichzeitig erfordert DNN einen großen Rechenaufwand und das Training dauert lange. Das Folgende ist ein einfaches Python-Codebeispiel, bei dem die Keras-Bibliothek zum Erstellen eines tiefen neuronalen Netzwerkmodells verwendet wird:

from keras.models import Sequentialfrom keras.layers import Densefrom keras.optimizers import Adamfrom keras.losses import BinaryCrossentropyimport numpy as np# 构建模型model = Sequential()model.add(Dense(64, activatinotallow='relu', input_shape=(10,))) # 输入层有10个特征model.add(Dense(64, activatinotallow='relu')) # 隐藏层有64个神经元model.add(Dense(1, activatinotallow='sigmoid')) # 输出层有1个神经元，使用sigmoid激活函数进行二分类任务# 编译模型model.compile(optimizer=Adam(lr=0.001), loss=BinaryCrossentropy(), metrics=['accuracy'])# 生成模拟数据集x_train = np.random.rand(1000, 10) # 1000个样本，每个样本有10个特征y_train = np.random.randint(2, size=1000) # 1000个标签，二分类任务# 训练模型model.fit(x_train, y_train, epochs=10, batch_size=32) # 训练10个轮次，每次使用32个样本进行训练

2. Symbolikmodell

Das Symbolikmodell ist eine intelligente Simulationsmethode, die auf logischem Denken basiert und davon ausgeht Menschen sind ein physisches Symbolsystem, und Computer sind auch physische Symbolsysteme. Daher können die Regelbasis und die Argumentationsmaschine des Computers verwendet werden, um menschliches intelligentes Verhalten zu simulieren, dh die symbolischen Operationen des Computers werden verwendet, um menschliche kognitive Prozesse zu simulieren. Um es ganz klar auszudrücken: Es bedeutet, menschliche Logik im Computer zu speichern, um eine intelligente Ausführung zu erreichen.

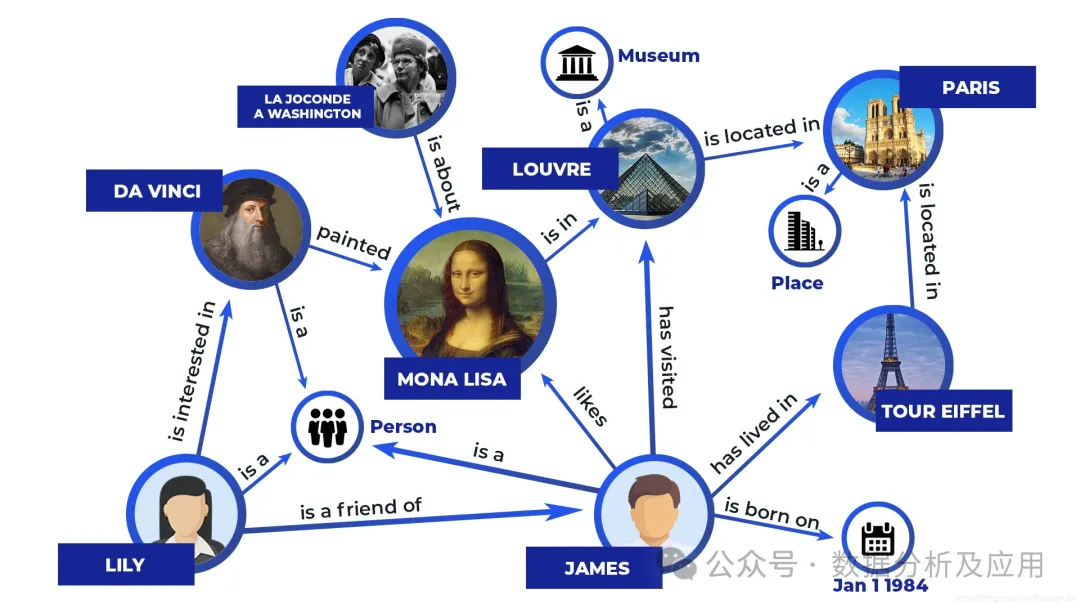
Zu den repräsentativen Modellen gehören Expertensysteme, Wissensdatenbanken und Wissensgraphen. Das Prinzip besteht darin, Informationen in einen Satz identifizierbarer Symbole zu kodieren und die Symbole mithilfe expliziter Regeln zu verarbeiten, um Operationsergebnisse zu erzeugen. Ein einfaches Beispiel für ein Expertensystem ist wie folgt:

# 定义规则库rules = [{"name": "rule1", "condition": "sym1 == 'A' and sym2 == 'B'", "action": "result = 'C'"},{"name": "rule2", "condition": "sym1 == 'B' and sym2 == 'C'", "action": "result = 'D'"},{"name": "rule3", "condition": "sym1 == 'A' or sym2 == 'B'", "action": "result = 'E'"},]# 定义推理引擎def infer(rules, sym1, sym2):for rule in rules:if rule["condition"] == True:# 条件为真时执行动作return rule["action"]return None# 没有满足条件的规则时返回None# 测试专家系统print(infer(rules, 'A', 'B'))# 输出: Cprint(infer(rules, 'B', 'C'))# 输出: Dprint(infer(rules, 'A', 'C'))# 输出: Eprint(infer(rules, 'B', 'B'))# 输出: E

三、决策树类的模型

决策树模型是一种非参数的分类和回归方法，它利用树形图表示决策过程。更通俗来讲，树模型的数学描述就是“分段函数”。它利用信息论中的熵理论选择决策树的最佳划分属性，以构建出一棵具有最佳分类性能的决策树。

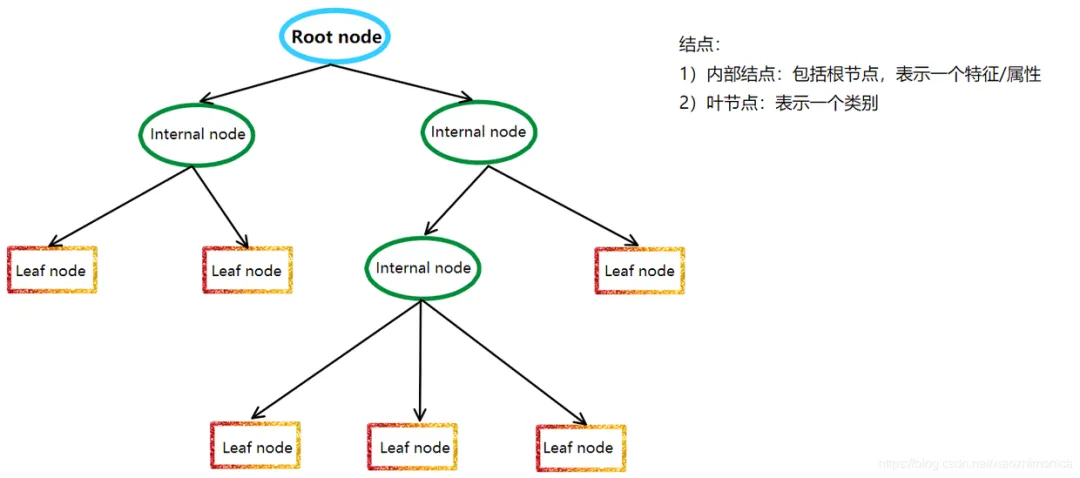
决策树模型的基本原理是递归地将数据集划分成若干个子数据集，直到每个子数据集都属于同一类别或者满足某个停止条件。在划分过程中，决策树模型采用信息增益、信息增益率、基尼指数等指标来评估划分的好坏，以选择最佳的划分属性。

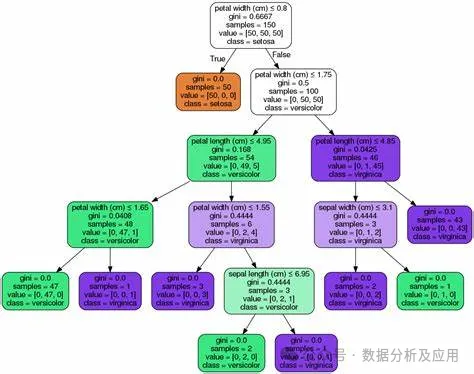
决策树模型的代表模型有很多，其中最著名的有ID3、C4.5、CART等。ID3算法是决策树算法的鼻祖，它采用信息增益来选择最佳划分属性；C4.5算法是ID3算法的改进版，它采用信息增益率来选择最佳划分属性，同时采用剪枝策略来提高决策树的泛化能力；CART算法则是分类和回归树的简称，它采用基尼指数来选择最佳划分属性，并能够处理连续属性和有序属性。

以下是使用Python中的Scikit-learn库实现CART算法的代码示例：

from sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitfrom sklearn.tree import DecisionTreeClassifier, plot_tree# 加载数据集iris = load_iris()X = iris.datay = iris.target# 划分训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 构建决策树模型clf = DecisionTreeClassifier(criterinotallow='gini')clf.fit(X_train, y_train)# 预测测试集结果y_pred = clf.predict(X_test)# 可视化决策树plot_tree(clf)

四、概率类的模型

概率模型是一种基于概率论的数学模型，用于描述随机现象或事件的分布、发生概率以及它们之间的概率关系。概率模型在各个领域都有广泛的应用，如统计学、经济学、机器学习等。

概率模型的原理基于概率论和统计学的基本原理。它使用概率分布来描述随机变量的分布情况，并使用概率规则来描述事件之间的条件关系。通过这些原理，概率模型可以对随机现象或事件进行定量分析和预测。

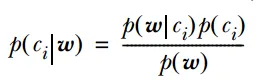
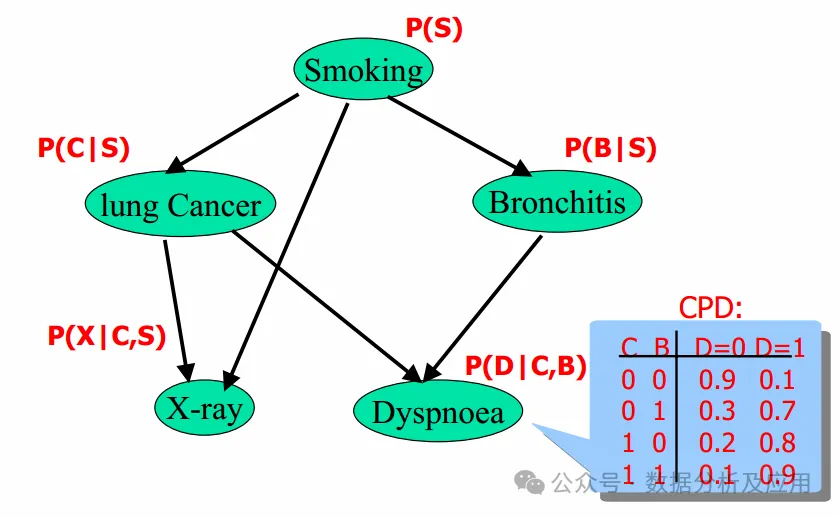
代表模型主要有：朴素贝叶斯分类器、贝叶斯网络、隐马尔可夫模型。其中，朴素贝叶斯分类器和逻辑回归都基于贝叶斯定理，它们都使用概率来表示分类的不确定性。

隐马尔可夫模型和贝叶斯网络都是基于概率的模型，可用于描述随机序列和随机变量之间的关系。

朴素贝叶斯分类器和贝叶斯网络都是基于概率的图模型，可用于描述随机变量之间的概率关系。

以下是使用Python中的Scikit-learn库实现朴素贝叶斯分类器的代码示例：

from sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitfrom sklearn.naive_bayes import GaussianNB# 加载数据集iris = load_iris()X = iris.datay = iris.target# 划分训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 构建朴素贝叶斯分类器模型clf = GaussianNB()clf.fit(X_train, y_train)# 预测测试集结果y_pred = clf.predict(X_test)

五、近邻类的模型

近邻类模型（本来想命名为距离类模型，但是距离类的定义就比较宽泛了）是一种非参数的分类和回归方法，它基于实例的学习不需要明确的训练和测试集的划分。它通过测量不同数据点之间的距离来决定数据的相似性。

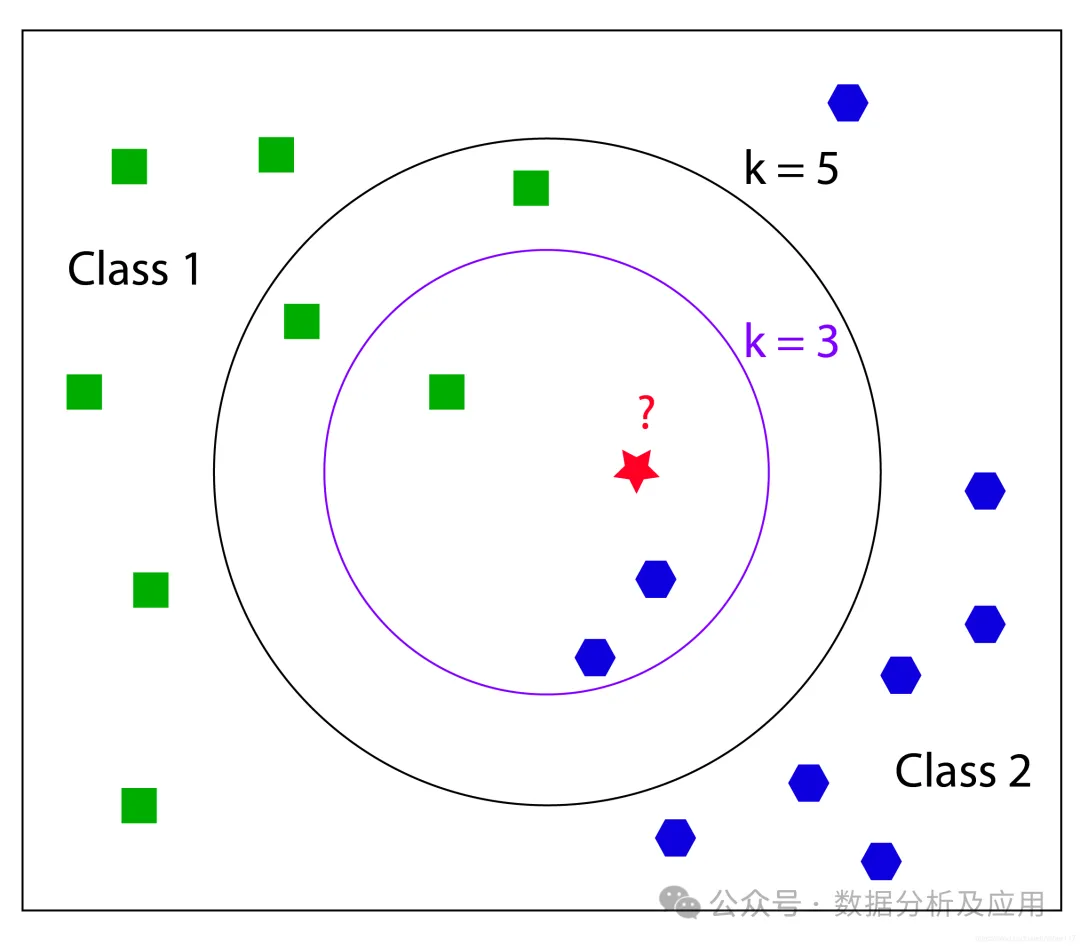
以KNN算法为例，其核心思想是，如果一个样本在特征空间中的 k 个最接近的训练样本中的大多数属于某一个类别，则该样本也属于这个类别。KNN算法基于实例的学习不需要明确的训练和测试集的划分，而是通过测量不同数据点之间的距离来决定数据的相似性。

代表模型有：k-近邻算法（k-Nearest Neighbors，KNN）、半径搜索（Radius Search）、K-means、权重KNN、多级分类KNN（Multi-level Classification KNN）、近似最近邻算法（Approximate Nearest Neighbor， ANN）

近邻模型基于相似的原理，即通过测量不同数据点之间的距离来决定数据的相似性。

除了最基础的KNN算法外，其他变种如权重KNN和多级分类KNN都在基础算法上进行了改进，以更好地适应不同的分类问题。

近似最近邻算法（ANN）是一种通过牺牲精度来换取时间和空间的方式，从大量样本中获取最近邻的方法。ANN算法通过降低存储空间和提高查找效率来处理大规模数据集。它通过“近似”的方法来减少搜索时间，这种方法允许在搜索过程中存在少量误差。

以下是使用Python中的Scikit-learn库实现KNN算法的代码示例：

from sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitfrom sklearn.neighbors import KNeighborsClassifier# 加载数据集iris = load_iris()X = iris.datay = iris.target# 划分训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 构建KNN分类器模型knn = KNeighborsClassifier(n_neighbors=3)knn.fit(X_train, y_train)# 预测测试集结果y_pred = knn.predict(X_test)

六、集成学习类的模型

集成学习（Ensemble Learning）不仅仅是一类的模型，更是一种多模型融合的思想，通过将多个学习器的预测结果进行合并，以提高整体的预测精度和稳定性。在实际应用中，集成学习无疑是数据挖掘的神器！

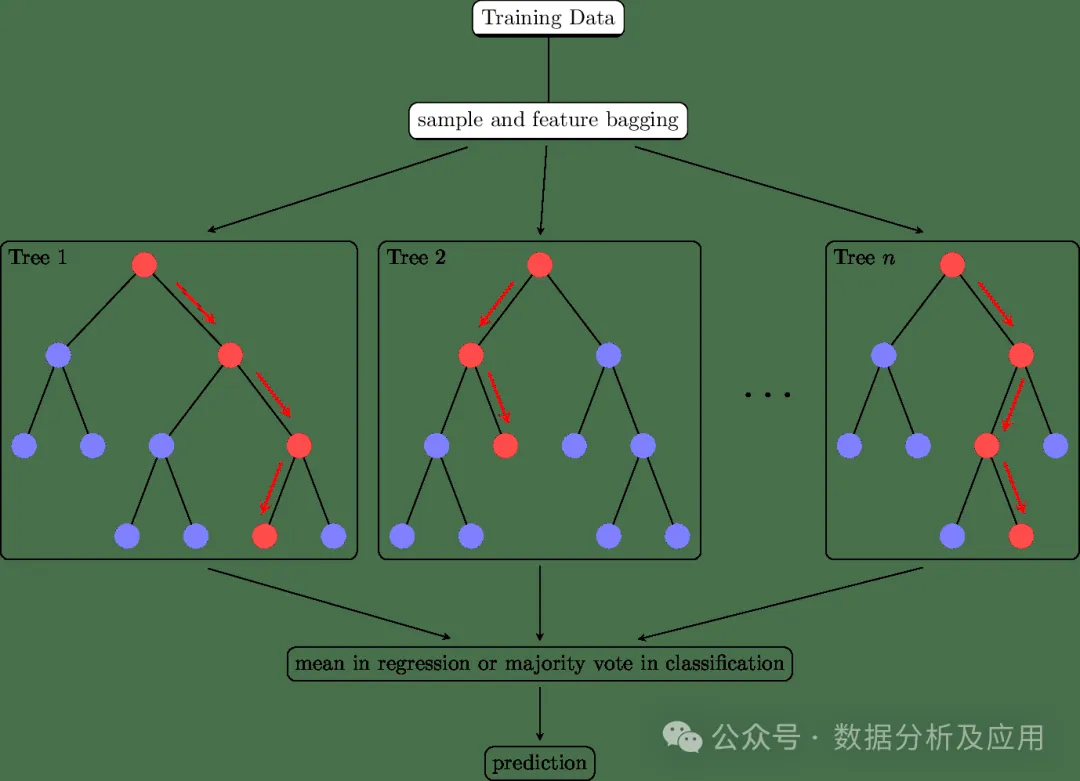
集成学习的核心思想是通过集成多个基学习器来提高整体的预测性能。具体来说，通过将多个学习器的预测结果进行合并，可以减少单一学习器的过拟合和欠拟合问题，提高模型的泛化能力。同时，通过引入多样性（如不同的基学习器、不同的训练数据等），可以进一步提高模型的性能。常用的集成学习方法有：

• Bagging是一种通过引入多样性和减少方差来提高模型稳定性和泛化能力的集成学习方法。它可以应用于任何分类或回归算法。
• Boosting是一种通过引入多样性和改变基学习器的重要性来提高模型性能的集成学习方法。它也是一种可以应用于任何分类或回归算法的通用技术。
• stack堆叠是一种更高级的集成学习方法，它将不同的基学习器组合成一个层次结构，并通过一个元学习器对它们进行整合。堆叠可以用于分类或回归问题，并通常用于提高模型的泛化能力。

集成学习代表模型有：随机森林、孤立森林、GBDT、Adaboost、Xgboost等。以下是使用Python中的Scikit-learn库实现随机森林算法的代码示例：

from sklearn.ensemble import RandomForestClassifierfrom sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_split# 加载数据集iris = load_iris()X = iris.datay = iris.target# 划分训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 构建随机森林分类器模型clf = RandomForestClassifier(n_estimators=100, random_state=42)clf.fit(X_train, y_train)# 预测测试集结果y_pred = clf.predict(X_test)

综上，我们通过将相似原理的模型归纳为各种类别，以此逐个类别地探索其原理，可以更为系统全面地了解模型的原理及联系。希望对大家有所帮助！

Das obige ist der detaillierte Inhalt vonTransparent! Eine ausführliche Analyse der Prinzipien der wichtigsten Modelle des maschinellen Lernens!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!