Heim >Technologie-Peripheriegeräte >KI >Studenten der Tsinghua Yao-Klasse veröffentlichten zwei Werke in Folge, die größte Verbesserung seit zehn Jahren: Die Matrixmultiplikation liegt nahe am theoretischen Optimum
Studenten der Tsinghua Yao-Klasse veröffentlichten zwei Werke in Folge, die größte Verbesserung seit zehn Jahren: Die Matrixmultiplikation liegt nahe am theoretischen Optimum
- 王林nach vorne
- 2024-03-08 21:52:02959Durchsuche
Durch die Beseitigung „versteckter Ineffizienzen“ haben Informatiker einen neuen Weg gefunden, große Matrizen schneller als je zuvor zu multiplizieren.
Als Grundoperation vieler GPU-Operatoren spielt die Matrixmultiplikation eine wichtige Rolle im Hochleistungsrechnen und ist auch eine Schlüsselkomponente von Anwendungen wie KI. Obwohl der Algorithmus selbst relativ einfach ist, wurden im Laufe der Jahre Anstrengungen unternommen, ihn zu optimieren, um höhere Geschwindigkeiten zu erreichen. Der Umfang der Optimierung war jedoch etwas begrenzt.
In der neuesten Ausgabe des Quantum Magazine haben wir zwei Artikel gefunden, die die Matrixmultiplikation beschleunigen können. An der Erstellung dieser beiden Arbeiten beteiligte sich ein älterer Student der Yao-Klasse der Tsinghua-Universität aktiv, was neue Perspektiven für die Verbesserung von Algorithmen in diesem Bereich eröffnete.
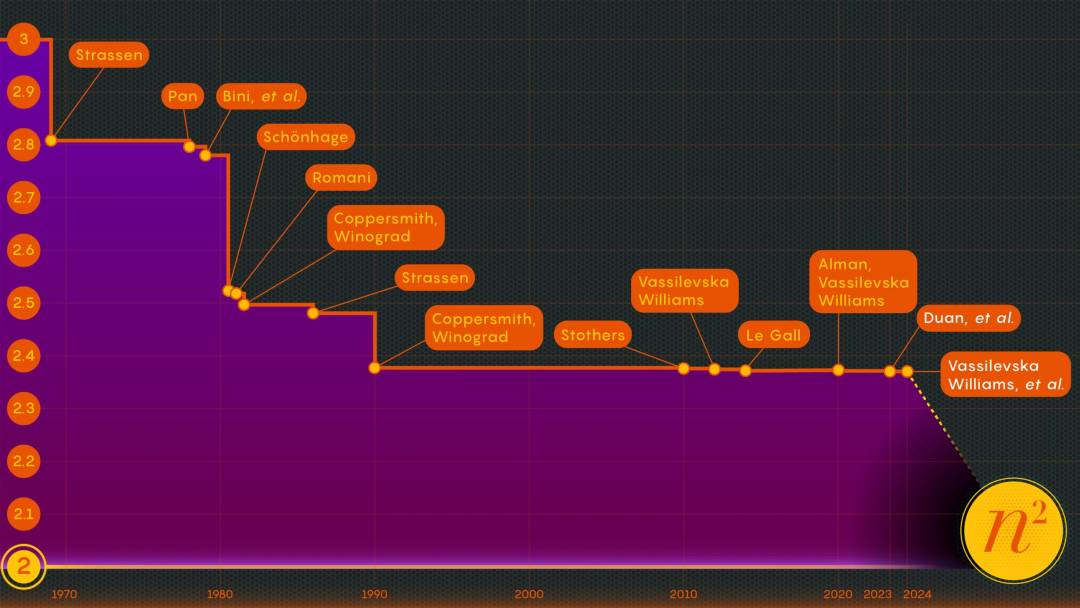
Eine neue „Singularität“ entsteht in der Verbesserung der Matrixmultiplikation
Informatiker sind eine sehr anspruchsvolle Gruppe von Menschen. Ihr Ziel ist es nicht nur, Probleme zu lösen, sondern Ziele auf möglichst effiziente Weise zu erreichen.
Nehmen Sie das Beispiel der Multiplikation von Matrizen oder Zahlenreihen. Im Jahr 1812 schlug der französische Mathematiker Jacques Philippe Marie Binet eine Reihe grundlegender Regeln vor, die den Schülern noch heute beigebracht werden. Dieses Regelwerk ist weit verbreitet, doch in den letzten Jahren haben einige Mathematiker Wege gefunden, den Prozess zu vereinfachen und zu beschleunigen. Französischer Mathematiker Jacques Philippe Marie Binet.

Ran Duan und Renfei Zhou von der Tsinghua University und Hongxun Wu von der University of California, Berkeley, erfordern, um dieses seit langem bestehende Problem zu lösen erstellt und ihre Forschungsergebnisse in einem 87-seitigen Papier ausführlich dargestellt. Le Gall lobte die Arbeit dieser drei Forscher. Er glaubte, dass die Verbesserung zwar relativ gering, aber ein beispielloser konzeptioneller Durchbruch sei. Dieser Beitrag wurde von FOCS 2023, der Top-Konferenz im Bereich Informatik, angenommen.
Paper v1 erscheint im Oktober 2022, v5 im November 2023. Adresse des Beitrags: https://arxiv.org/abs/2210.10173
Duan Ran ist unter anderem außerordentlicher Professor am Institut für Cross-Information der Tsinghua-Universität. Seine Forschungsschwerpunkte sind Graphentheorie-Algorithmen, Datenstrukturen und Informatik Theorie. Hongxun Wu ist Doktorand im zweiten Jahr an der University of California, Berkeley und Absolvent der Yao-Klasse der Tsinghua-Universität.

Das Paper von drei Forschern deckt bisher unbekannte und ungenutzte Potenziale für Verbesserungen auf, die bereits Früchte tragen. Ein zweites im Januar 2024 veröffentlichtes Papier (ebenfalls Co-Autor von Renfei Zhou) baut darauf auf und zeigt, wie die Matrixmultiplikation weiter verbessert werden kann.
 Papieradresse: https://epubs.siam.org/doi/10.1137/1.9781611977912.134
Papieradresse: https://epubs.siam.org/doi/10.1137/1.9781611977912.134William Kuszmaul, ein theoretischer Informatiker an der Harvard University, sagte, dass dies ein großer technologischer Durchbruch sei, mehr als zehn Die größte Verbesserung, die wir seit Jahren bei der Matrixmultiplikation gesehen haben.
 Welches Problem sollte bei der Matrixmultiplikation verbessert werden?
Welches Problem sollte bei der Matrixmultiplikation verbessert werden?Matrixmultiplikation mag wie ein obskures Problem erscheinen, aber es ist eine grundlegende Rechenoperation. Es ist in die meisten Algorithmen integriert, die Menschen täglich für eine Vielzahl von Aufgaben verwenden, von der Anzeige klarerer Computergrafiken bis hin zur Lösung logistischer Probleme in der Netzwerktheorie. Wie in anderen Bereichen der Informatik ist Geschwindigkeit von entscheidender Bedeutung. Selbst kleine Verbesserungen könnten letztendlich den Zeit-, Rechenleistungs- und Geldaufwand deutlich reduzieren. Doch vorerst geht es den Theoretikern vor allem darum, herauszufinden, wie schnell der Prozess ablaufen kann.
Die traditionelle Methode der Multiplikation zweier n×n-Matrizen – also die Multiplikation der Zahlen in jeder Zeile der ersten Matrix mit den Zahlen in jeder Spalte der zweiten Matrix – erfordert n³ unabhängige Multiplikationsoperationen. Für eine 2 x 2-Matrix bedeutet dies 2³ oder 8 Multiplikationen.
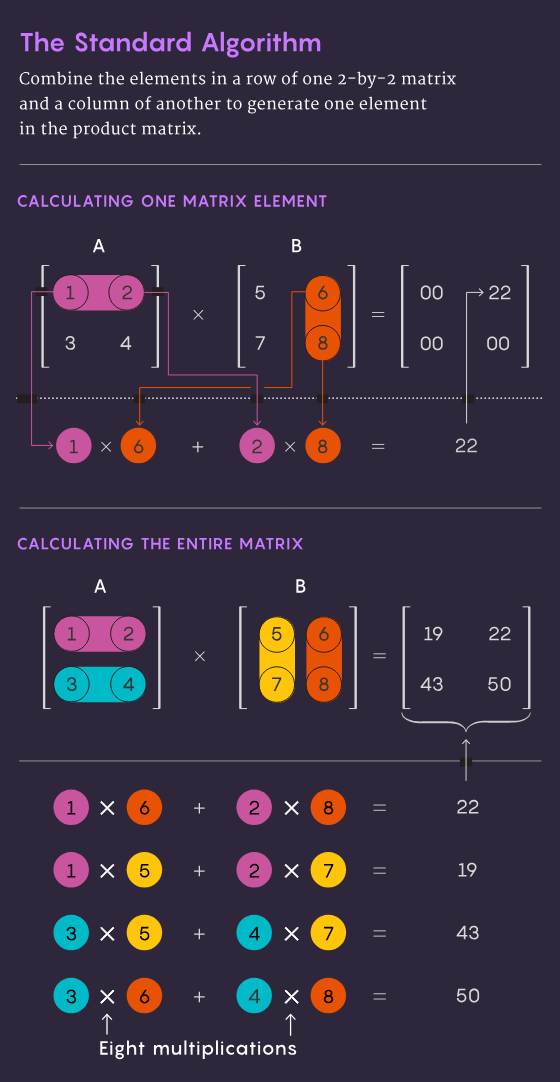
1969 entdeckte der Mathematiker Volker Strassen eine elegantere Methode, mit der die Multiplikation von 2×2-Matrizen in nur 7 Multiplikationsschritten und 18 Additionsschritten durchgeführt werden kann. Zwei Jahre später zeigte der Informatiker Shmuel Winograd, dass eine 7-stufige Multiplikation tatsächlich das absolute Minimum für eine 2×2-Matrix war.
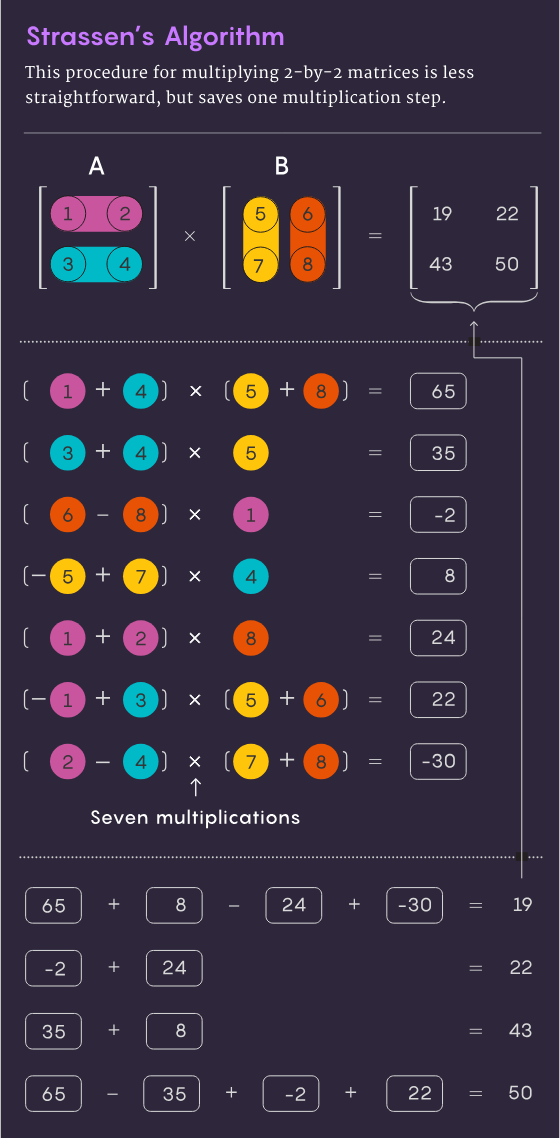
Strassen nutzte die gleiche Idee, um zu zeigen, dass alle größeren n×n-Matrizen auch in weniger als n3 Schritten multipliziert werden können. Ein Schlüsselelement dieser Strategie ist ein Verfahren namens Zerlegung: die Zerlegung einer großen Matrix in kleinere Untermatrizen, die am Ende nur 2×2 oder sogar 1×1 (nur eine einzelne Zahl) betragen können.
Der Grund dafür, riesige Arrays in kleine Stücke zu zerlegen, ist ganz einfach: „Eine große Matrix (z. B. eine 100×100-Matrix) ist für Menschen schwer vorstellbar.“ der beste Algorithmus.“ Selbst die 3 x 3-Matrix ist noch nicht vollständig gelöst. „Man kann jedoch schnelle Algorithmen verwenden, die für kleine Matrizen entwickelt wurden, um schnelle Algorithmen für größere Matrizen zu erhalten.“
Die Forscher stellten fest, dass der Schlüssel zur Geschwindigkeit darin besteht, die Anzahl der Multiplikationsschritte zu reduzieren und den Exponenten von n3 um so viel zu verschieben wie möglich (traditionelle Methode) reduzieren. Der kleinstmögliche Wert n² ist im Grunde die Zeit, die zum Schreiben der Antwort benötigt wird. Informatiker nennen diesen Exponenten Ω oder ω. nω ist die Mindestanzahl von Schritten, die erforderlich sind, um zwei n×n-Matrizen erfolgreich zu multiplizieren, wenn n größer wird. Zhou Renfei, der auch Mitautor des Artikels vom Januar 2024 ist, sagte: „Der Schwerpunkt dieser Arbeit liegt darauf, herauszufinden, wie nahe man an 2 herankommen kann und ob dies theoretisch erreichbar ist.“
1986 gelang Strassen ein weiterer großer Durchbruch, als er die Lasermethode der Matrixmultiplikation einführte. Strassen ermittelte daraus einen oberen Grenzwert für ω von 2,48. Obwohl die Methode nur ein Schritt in der Multiplikation großer Matrizen ist, ist sie einer der wichtigsten, da Forscher sie ständig verbessern.Ein Jahr später führten Winograd und Don Coppersmith einen neuen Algorithmus ein, der die Lasermethode perfekt ergänzte. Diese Kombination von Werkzeugen wurde in fast allen nachfolgenden Forschungen zur Beschleunigung der Matrixmultiplikation verwendet.
Hier ist eine vereinfachte Darstellung, wie diese verschiedenen Elemente zusammenpassen. Beginnen wir mit zwei großen Matrizen A und B und multiplizieren sie. Zuerst zerlegen Sie sie in viele kleinere Untermatrizen, manchmal auch Blöcke genannt. Als nächstes können Sie die Algorithmen von Coppersmith und Winograd als Leitfaden für die Verarbeitung und schließlich den Zusammenbau dieser Blöcke verwenden. „Es sagt mir, was ich multiplizieren muss, was ich hinzufügen soll und welche Elemente sich wo in der Produktmatrix C befinden“, sagte Vassilevska Williams. „Es ist nur ein ‚Rezept‘ für den Aufbau von C aus A und B.“ Es gibt jedoch ein Problem: Manchmal erhält man Blöcke mit gemeinsamen Elementen. Die Beibehaltung dieser gemeinsamen Elemente käme einer doppelten Zählung dieser Elemente gleich, daher müssen diese Überschneidungen irgendwann beseitigt werden. Die Forscher lösten dieses Problem, indem sie die Blöcke, in denen sie sich befanden, „töteten“ und ihre Komponenten auf Null setzten, um sie aus der Berechnung zu entfernen.
Hier kommt endlich die Lasermethode von Strassen ins Spiel. „Die Lasermethode ist normalerweise sehr effektiv und findet oft eine gute Möglichkeit, überlappende Teilblöcke zu beseitigen“, sagte Le Gall. Nachdem der Laser alle Überlappungen beseitigt hat, können Sie die endgültige Produktmatrix C erstellen. Die Kombination dieser verschiedenen Techniken führt zu einem Algorithmus, der zwei Matrizen mit möglichst wenigen Gesamtmultiplikationen multipliziert, zumindest theoretisch. Die Lasermethode ist nicht für praktische Anwendungen gedacht; sie ist lediglich eine ideale Denkweise für die Matrixmultiplikation. Zhou Renfei sagte: „Wir haben diese Methode noch nie auf einem Computer ausgeführt, wir analysieren sie.“ Diese Analyse hat zur größten Verbesserung von ω seit mehr als zehn Jahren beigetragen. In der ersten Arbeit „Faster Matrix Multiplication via Asymmetric Hashing“ von Duan Ran, Zhou Renfei und Hongxun Wu zeigten sie, dass der Prozess des Strassen-Algorithmus erheblich beschleunigt werden kann. Dies alles ist einem Konzept zu verdanken, das sie „versteckter Verlust“ nennen. Zhou Renfei sagte, dass das Konzept in früheren Analysen tief verborgen war und das Ergebnis der versehentlichen Beseitigung zu vieler Blöcke war. Bei der Lasermethode werden überlappende Blöcke als Müll markiert und zur Verarbeitung eingeplant, während andere Blöcke als wertvoll gelten und gespeichert werden. Allerdings ist der Auswahlprozess etwas zufällig. Tatsächlich können als Müll markierte Blöcke am Ende nützlich sein. Das ist nicht ganz überraschend, aber durch die Untersuchung vieler zufälliger Auswahlen stellte Duan Rans Team fest, dass die Lasermethode den Wert von Blöcken systematisch unterschätzt, sodass mehr Blöcke gespeichert und weniger weggeworfen werden sollten. Und wie so oft führt weniger Abfall zu mehr Effizienz. In Bezug auf den Ansatz von Duan Ran glaubt Le Gall, dass „mehr Blöcke ohne Überlappung erhalten bleiben können“. Nachdem das Team von Duan Ran die Existenz dieses Verlusts nachgewiesen hat, hat es die Art und Weise modifiziert, wie der Laser funktioniert Methode markiert Blöcke und reduziert so den Abfall deutlich. Sie haben eine neue Obergrenze für ω auf etwa 2,371866 festgelegt, was eine Verbesserung gegenüber der von Josh Alman und Vassilevska Williams im Jahr 2020 festgelegten Obergrenze von 2,3728596 darstellt. Dies mag wie eine kleine Änderung erscheinen, . Im Vergleich dazu verbesserten sich die Ergebnisse von Vassilevska Williams und Alman im Jahr 2020 gegenüber ihren vorherigen Ergebnissen nur um 0,00001. Laut Le Gall verlassen sich seit fast vier Jahrzehnten alle auf die gleiche Lasermethode. Mit dem Aufkommen von Arbeiten von drei Forschern, darunter Duan Ran, können wir es besser machen. Daher hat das von Zhou Renfei mitverfasste Papier vom Januar 2024 diese neue Methode verbessert und den versteckten Verlust weiter reduziert. Sie erhöhten die Obergrenze von ω weiter und senkten sie auf 2,371552
Originallink: https://www.quantamagazine.org/new-breakthrough-brings-matrix-multiplication-closer-to-ideal-20240307/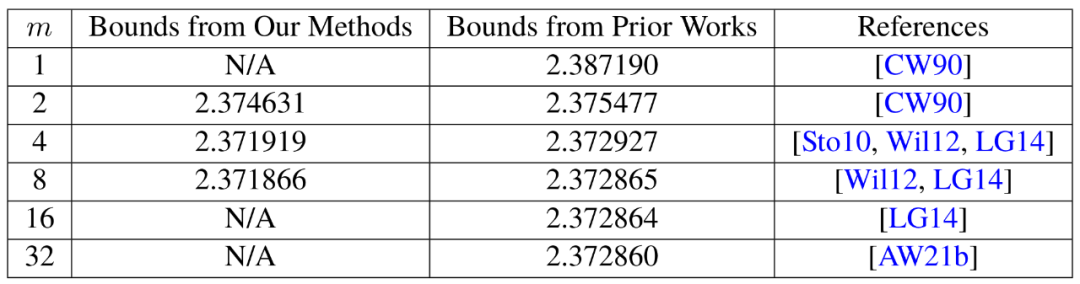 Das Aufregendste für die Forscher war natürlich nicht nur der neue Rekord selbst, der nicht lange anhielt. Tatsächlich zeigt dieses Papier einen neuen Weg zur Verbesserung auf, der zuvor völlig unbemerkt blieb.
Das Aufregendste für die Forscher war natürlich nicht nur der neue Rekord selbst, der nicht lange anhielt. Tatsächlich zeigt dieses Papier einen neuen Weg zur Verbesserung auf, der zuvor völlig unbemerkt blieb. 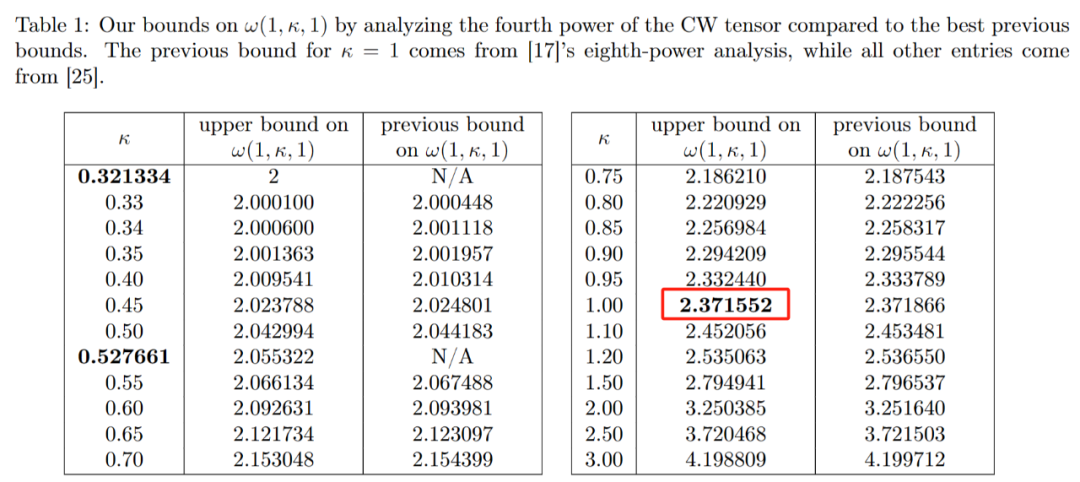
Das obige ist der detaillierte Inhalt vonStudenten der Tsinghua Yao-Klasse veröffentlichten zwei Werke in Folge, die größte Verbesserung seit zehn Jahren: Die Matrixmultiplikation liegt nahe am theoretischen Optimum. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

