Heim >Technologie-Peripheriegeräte >KI >Schrams Sortieren – Sortieren nach Fairness lernen
Schrams Sortieren – Sortieren nach Fairness lernen
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2024-02-07 14:50:31744Durchsuche
Auf der internationalen akademischen Konferenz AIBT 2023 im Jahr 2023 veröffentlichte Ratidar Technologies LLC einen fairnessbasierten Ranking-Lernalgorithmus und gewann den Preis für den besten Papierbericht der Konferenz. Der Algorithmus mit dem Namen Skellam Rank nutzt statistische Prinzipien voll aus und kombiniert Pairwise Ranking und Matrixzerlegungstechnologie, um die Genauigkeits- und Fairnessprobleme im Empfehlungssystem zu lösen. Da es in Empfehlungssystemen nur wenige innovative Ranking-Lernalgorithmen gibt, schnitt der Ranking-Algorithmus von Schramam so gut ab, dass er auf der Konferenz einen Forschungspreis gewann. Im Folgenden werden die Grundprinzipien des Schram-Algorithmus vorgestellt:
Erinnern wir uns zunächst an die Poisson-Verteilung:
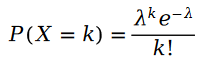
Die Berechnungsformel der Parameter der Poisson-Verteilung lautet wie folgt:
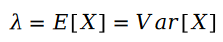
Zwei Der Unterschied zwischen Poisson-Variablen ist die Schram-Verteilung:
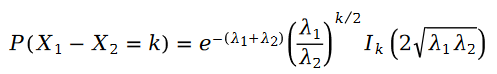
In der Formel gilt:
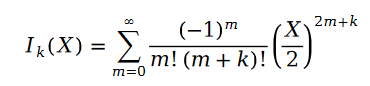
Die Funktion wird Bessel-Funktion erster Art genannt.
Lassen Sie uns mit diesen grundlegendsten Konzepten der Statistik ein Pairwise-Ranking-Ranking-Lernempfehlungssystem aufbauen!
Wir glauben zunächst, dass die Bewertung von Artikeln durch den Benutzer ein Poisson-Verteilungskonzept ist. Mit anderen Worten, der Bewertungswert des Benutzerelements folgt der folgenden Wahrscheinlichkeitsverteilung:
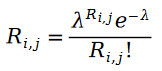
Der Grund, warum wir den Prozess der Benutzerbewertung von Elementen als Poisson-Prozess beschreiben können, liegt darin, dass es bei der Benutzerelementbewertung einen Matthew-Effekt gibt. Das heißt, Benutzer mit höheren Bewertungen haben mehr Bewertungen, sodass wir die Anzahl der Personen, die einen Artikel bewerten, verwenden können, um die Verteilung der Bewertungen für diesen Artikel anzunähern. Welchem zufälligen Prozess folgt die Anzahl der Personen, die einen Artikel bewerten? Natürlich werden wir an den Poisson-Prozess denken. Da die Wahrscheinlichkeit, dass ein Benutzer einen Artikel bewertet, der Wahrscheinlichkeit ähnelt, wie viele Personen den Artikel bewertet haben, können wir natürlich den Poisson-Prozess verwenden, um den Prozess der Benutzerbewertung eines Artikels anzunähern.
Wir werden die Parameter des Poisson-Prozesses durch die Statistiken der Beispieldaten ersetzen und die folgende Formel erhalten:
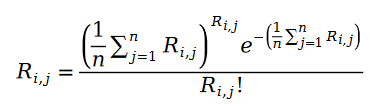
Wir werden unten die Maximum-Likelihood-Funktionsformel des Pariwise-Rankings definieren. Wie wir alle wissen, bedeutet das sogenannte Pairwise Ranking, dass wir die Maximum-Likelihood-Funktion zur Lösung der Modellparameter verwenden, sodass das Modell die Beziehung der bekannten Ranking-Paare in der Datenstichprobe weitestgehend aufrechterhalten kann:
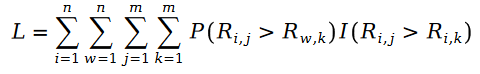
weil R in der Formel eine Poisson-Verteilung ist, ist ihr Unterschied also die Schramam-Verteilung, d Rufen Sie die Schramam-Verteilung auf. Die Formel wird in die Verlustfunktion L der Maximum-Likelihood-Funktion eingebracht und die folgende Formel erhalten:
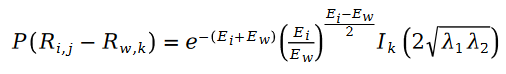
Im Benutzerbewertungswert R, der in der Variablen E erscheint, verwenden wir die Matrixzerlegung um es zu lösen. Verwenden Sie den Parameter Benutzermerkmalsvektor U und den Artikelmerkmalsvektor V in der Matrixzerlegung als zu lösende Variablen:
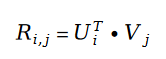
Hier überprüfen wir zunächst das Konzept der Matrixfaktorisierung. Das Konzept der Matrixfaktorisierung ist ein Empfehlungssystemalgorithmus, der um 2010 vorgeschlagen wurde. Dieser Algorithmus kann als einer der erfolgreichsten Empfehlungssystemalgorithmen in der Geschichte bezeichnet werden. Bis heute verwenden viele Empfehlungssystemunternehmen immer noch den Matrixzerlegungsalgorithmus als Basis für Online-Systeme, und Factorization Machine, eine wichtige Komponente im beliebten klassischen Empfehlungsalgorithmus DeepFM, ist auch eine nachfolgende Verbesserung des Matrixzerlegungsalgorithmus in der Die Version des Empfehlungssystems ist untrennbar mit der Matrixzerlegung verbunden. Es gibt eine wegweisende Arbeit zum Matrixfaktorisierungsalgorithmus, nämlich Probabilistic Matrix Factorization aus dem Jahr 2007. Der Autor nutzte ein statistisches Lernmodell, um das Konzept der Matrixfaktorisierung in der linearen Algebra umzugestalten und gab der Matrixfaktorisierung erstmals eine solide mathematisch-theoretische Grundlage.
Das Grundkonzept der Matrixzerlegung besteht darin, das Skalarprodukt von Vektoren zu verwenden, um unbekannte Benutzerbewertungen effizient vorherzusagen und gleichzeitig die Dimensionalität der Benutzerbewertungsmatrix zu reduzieren. Die Verlustfunktion der Matrixzerlegung lautet wie folgt:
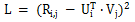
Es gibt viele Varianten des Matrixzerlegungsalgorithmus. Beispielsweise modelliert das von der Shanghai Jiao Tong University vorgeschlagene SVDFeature die Vektoren U und V in Form von Linearkombinationen , so dass das Matrixzerlegungsproblem zum Problem des Feature-Engineerings wird. SVDFeature ist auch ein wegweisendes Papier auf dem Gebiet der Matrixfaktorisierung. Die Matrixzerlegung kann beim Pairwise Ranking angewendet werden, um unbekannte Benutzerbewertungen zu ersetzen, um Modellierungszwecke zu erreichen. Zu den klassischen Anwendungsfällen gehört der BPR-MF-Algorithmus im Bayesian Pairwise Ranking, und der Schramam-Ranking-Algorithmus basiert auf denselben Ideen.
Wir verwenden den stochastischen Gradientenabstieg, um den Schramam-Sortieralgorithmus zu lösen. Da der stochastische Gradientenabstieg die Verlustfunktion im Lösungsprozess erheblich vereinfachen kann, um den Zweck der Lösung zu erreichen, wird unsere Verlustfunktion zu der folgenden Formel:
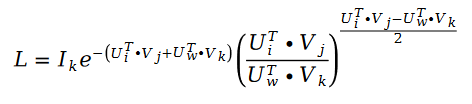
Verwenden Sie den stochastischen Gradientenabstieg, um die unbekannten Parameter U und Lösung nach V zu berechnen , erhalten wir die iterative Formel wie folgt:
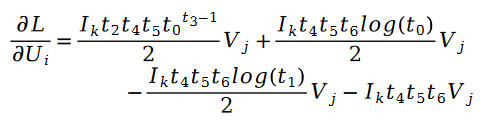
Unter ihnen:
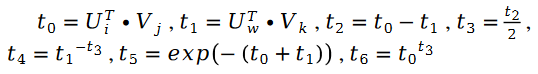
Zusätzlich:
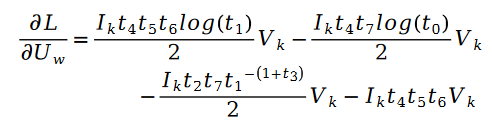
unter ihnen:
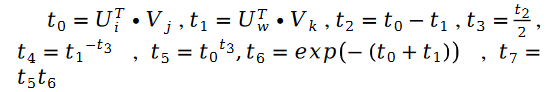
Für unbekannte Parametervariablen Die Lösung von V ist ähnlich, wir haben die folgende Formel:
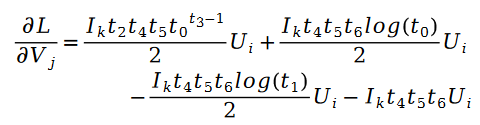
Darunter:
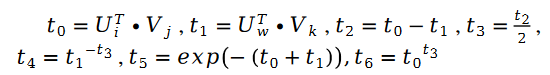
Zusätzlich:
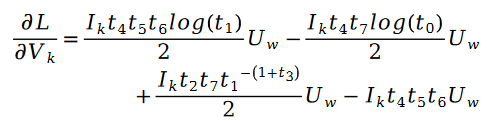
darunter:
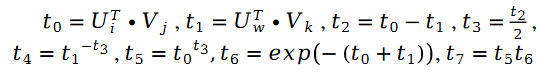
Den gesamten Algorithmusprozess verwenden wir zur Demonstration des folgenden Pseudocodes:

Um die Wirksamkeit des Algorithmus zu überprüfen, hat der Autor des Papiers ihn mit dem MovieLens 1 Million Dataset und dem LDOS-CoMoDa Dataset getestet. Der erste Datensatz enthält Bewertungen von 6040 Nutzern und 3706 Filmen. Der gesamte Bewertungsdatensatz umfasst ca. 1 Million Bewertungsdaten und ist eine der bekanntesten Bewertungsdatensammlungen im Bereich Empfehlungssysteme. Die zweite Datensammlung stammt aus Slowenien und ist eine im Internet seltene szenariobasierte Empfehlungssystem-Datensammlung. Der Datensatz enthält Bewertungen von 121 Nutzern und 1232 Filmen. Der Autor verglich Schrams Sortierung mit 9 anderen Empfehlungssystemalgorithmen. Die wichtigsten Bewertungsindikatoren sind MAE (mittlerer absoluter Fehler, verwendet zum Testen der Genauigkeit) und Grad des Matthew-Effekts (hauptsächlich verwendet zum Testen der Fairness):
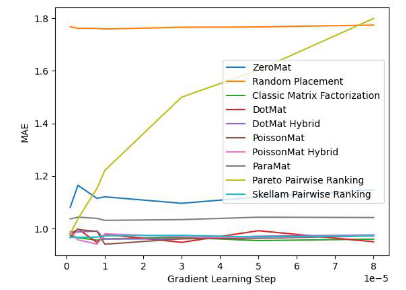
Abbildung 1 . MovieLens 1 Million Datensatz (MAE-Indikator)
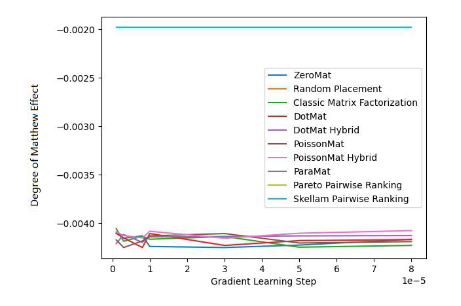
Abbildung 2. MovieLens 1 Million Datensatz (Grad des Matthew-Effekt-Indikators)
Anhand von Abbildung 1 und Abbildung 2 haben wir festgestellt, dass Schrams Sortierung beim MAE gut funktioniert Indikator, aber während des gesamten Experiments von Grid Search konnte nicht immer garantiert werden, dass die Leistung besser ist als bei anderen Algorithmen. Aber in Abbildung 2 stellen wir fest, dass Schrams Sortierung im Fairness-Index führend ist, weit vor den anderen 9 Empfehlungssystemalgorithmen.
Werfen wir einen Blick auf die Leistung dieses Algorithmus im LDOS-CoMoDa-Datensatz:
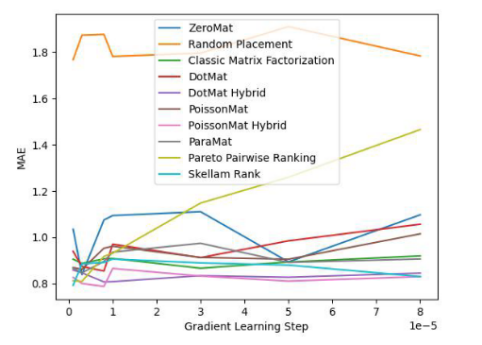
Abbildung 3. LDOS-CoMoDa-Datensatz (MAE-Indikator)
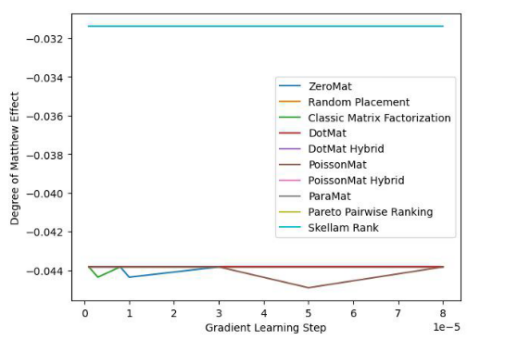
Abbildung 4. LDOS-CoMoDa-Datensatz (Grad des Matthew-Effekt-Indikators)
Anhand Abbildung 3 und Abbildung 4 verstehen wir, dass die Schillam-Sortierung beim Fairness-Indikator am besten ist und beim Genauigkeitsindikator gut abschneidet. Die Schlussfolgerung ähnelt dem vorherigen Experiment.
Schramm-Sortierung kombiniert Konzepte wie Poisson-Verteilung, Matrixzerlegung und paarweises Ranking und ist ein seltener Ranking-Lernalgorithmus für Empfehlungssysteme. Im technischen Bereich machen diejenigen, die die Ranking-Lerntechnologie beherrschen, nur 1/6 derjenigen aus, die Deep Learning beherrschen, sodass Ranking-Lernen eine knappe Technologie ist. Und es gibt noch weniger Talente, die originelles Ranking-Lernen im Bereich Empfehlungssysteme erfinden können. Der Ranking-Lernalgorithmus befreit Menschen von der engen Perspektive der Punktevorhersage und macht ihnen klar, dass das Wichtigste die Reihenfolge und nicht die Punktzahl ist. Auf Fairness basierendes Ranking-Lernen erfreut sich derzeit großer Beliebtheit im Bereich der Informationsbeschaffung, insbesondere auf Top-Konferenzen wie SIGIR. Beiträge zu Empfehlungssystemen auf Basis von Fairness sind sehr willkommen und hoffen, die Aufmerksamkeit der Leser zu erregen.
Über den Autor
Wang Hao, ehemaliger Leiter des Funplus Artificial Intelligence Laboratory. Er hatte Führungspositionen im Bereich Technologie und Technologie bei ThoughtWorks, Douban, Baidu, Sina und anderen Unternehmen inne. Da er 12 Jahre lang in Internetunternehmen, Finanztechnologie, Gaming und anderen Unternehmen gearbeitet hat, verfügt er über tiefe Einblicke und reiche Erfahrung in Bereichen wie künstliche Intelligenz, Computergrafik und Blockchain. Veröffentlichte 42 Artikel auf internationalen wissenschaftlichen Konferenzen und Fachzeitschriften und gewann den IEEE SMI 2008 Best Paper Award und den ICBDT 2020 / IEEE ICISCAE 2021 / AIBT 2023 Best Paper Report Award.
Das obige ist der detaillierte Inhalt vonSchrams Sortieren – Sortieren nach Fairness lernen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

