Anwendung des Baum-Welch-Algorithmus im impliziten Markov-Modell

Das implizite Markov-Modell (HMM) ist ein häufig verwendetes statistisches Modell zur Modellierung und Prognose von Zeitreihendaten. Der Baum-Welch-Algorithmus, auch Vorwärts-Rückwärts-Algorithmus genannt, ist ein unbeaufsichtigter Lernalgorithmus, der zur HMM-Parameterschätzung verwendet wird. In diesem Artikel werden das Prinzip und der Implementierungsprozess des Baum-Welch-Algorithmus ausführlich vorgestellt.
1. Einführung in HMM
Bevor wir den Baum-Welch-Algorithmus vorstellen, wollen wir zunächst das HMM-Modell verstehen. Das HMM-Modell ist ein probabilistisches Modell, mit dem der Prozess der zufälligen Generierung von Beobachtungssequenzen durch versteckte Markov-Ketten beschrieben wird. Eine versteckte Markov-Kette besteht aus einer Reihe von Zuständen und Übergangswahrscheinlichkeiten zwischen Zuständen, und die Beobachtungssequenz besteht aus den von jedem Zustand erzeugten Beobachtungen. Die Grundannahme des HMM-Modells besteht darin, dass jeder Beobachtungswert in der Beobachtungssequenz nur vom aktuellen Zustand abhängt und nichts mit vergangenen Zuständen und Beobachtungen zu tun hat. Der Baum-Welch-Algorithmus ist ein unbeaufsichtigter Lernalgorithmus, der zur Schätzung der Parameter von HMM-Modellen verwendet wird. Es passt die Übergangswahrscheinlichkeit und Emissionswahrscheinlichkeit des Modells iterativ entsprechend der Beobachtungssequenz an, sodass das Modell besser an die Beobachtungsdaten angepasst werden kann. Durch mehrere Iterationen kann der Baum-Welch-Algorithmus die optimalen Modellparameter finden und dadurch den Generierungsprozess der Beobachtungssequenz genauer beschreiben.
HMM-Modell kann durch drei Parameter beschrieben werden:
1. Der Anfangszustandswahrscheinlichkeitsvektor (π) stellt die Anfangszustandswahrscheinlichkeitsmatrix (A) dar. , die die Wahrscheinlichkeit des Übergangs von einem Zustand in einen anderen darstellt
3, die die Wahrscheinlichkeit angibt, in jedem Zustand einen Beobachtungswert zu erzeugen.
HMM-Modelle verwenden normalerweise Vorwärts- und Rückwärtsalgorithmen für Vorhersage und Schlussfolgerung. Allerdings müssen drei Parameter im HMM-Modell aus Trainingsdaten geschätzt werden. Genau das macht der Baum-Welch-Algorithmus.
2. Prinzip des Baum-Welch-Algorithmus
Der Baum-Welch-Algorithmus ist ein unbeaufsichtigter Lernalgorithmus basierend auf dem EM-Algorithmus, der zur Schätzung der drei Parameter des HMM-Modells verwendet wird. Der EM-Algorithmus ist ein iterativer Algorithmus, der die Wahrscheinlichkeitsfunktion zur Lösung von Parametern durch abwechselnde E-Schritte und M-Schritte maximiert. Im HMM berechnet der E-Schritt die Wahrscheinlichkeit, sich zu jedem Zeitpunkt in jedem Zustand zu befinden, wenn die aktuellen Parameter vorliegen. Der M-Schritt aktualisiert die Modellparameter anhand dieser Wahrscheinlichkeiten.
Im Einzelnen ist der Prozess des Baum-Welch-Algorithmus wie folgt:
1. Modellparameter (π, A, B) zufällig initialisieren;
2 die aktuellen Parameter, die Wahrscheinlichkeit, sich zu jedem Zeitpunkt in jedem Zustand zu befinden;
3 Verwenden Sie diese Wahrscheinlichkeiten, um die Modellparameter zu aktualisieren, insbesondere den Anfangszustandswahrscheinlichkeitsvektor π, die Zustandsübergangswahrscheinlichkeitsmatrix A und die Beobachtungswahrscheinlichkeitsmatrix B ;
4. Wiederholen Sie die Schritte 2 und 3, bis die Modellparameter übereinstimmen.
In Schritt E müssen wir die Wahrscheinlichkeit berechnen, dass wir uns angesichts der aktuellen Parameter zu jedem Zeitpunkt in jedem Zustand befinden. Konkret müssen wir die Vorwärtswahrscheinlichkeit α und die Rückwärtswahrscheinlichkeit β berechnen:
α_t(i)=P(O_1,O_2,…,O_t,q_t=i|λ)
β_t(i) =P (O_t+1,O_t+2,…,O_T|q_t=i,λ)
wobei λ die aktuellen Modellparameter darstellt, O die Beobachtungswertsequenz darstellt und q die Zustandssequenz darstellt. α_t(i) stellt die Wahrscheinlichkeit dar, zum Zeitpunkt t im Zustand i zu sein, und β_t(i) stellt die Wahrscheinlichkeit der Beobachtungssequenz vom Zeitpunkt t+1 bis zum Zeitpunkt T unter gegebener Bedingung des Zustands i dar. α und β können rekursiv berechnet werden.
In Schritt M müssen wir diese Wahrscheinlichkeiten verwenden, um die Modellparameter zu aktualisieren. Insbesondere müssen wir den neuen Anfangszustandswahrscheinlichkeitsvektor π, die Zustandsübergangswahrscheinlichkeitsmatrix A und die Beobachtungswahrscheinlichkeitsmatrix B berechnen:
π_i=α_1(i)β_1(i)/P(O|λ)
A_ij=∑_(t=1)^(T-1)α_t(i)a_ij b_j(O_t+1)β_t+1(j)/∑_(t=1)^(T-1)α_t(i ) β_t(i)
B_j(k)=∑_(t=1)^(T-1)γ_t(j,k)/∑_(t=1)^(T-1)γ_t(j )
Unter diesen stellt γ_t(i,j) die Wahrscheinlichkeit dar, zum Zeitpunkt t im Zustand i und zum Zeitpunkt t+1 im Zustand j zu sein, und P(O|λ) stellt die Wahrscheinlichkeit der Beobachtungssequenz dar. Mit diesen Formeln können Sie Modellparameter aktualisieren.
Die Konvergenz des Baum-Welch-Algorithmus ist garantiert, er kann jedoch zu einer lokalen optimalen Lösung konvergieren. Um diese Situation zu vermeiden, ist es normalerweise erforderlich, den Baum-Welch-Algorithmus mehrmals auszuführen und die optimalen Modellparameter auszuwählen.
3. Implementierung des Baum-Welch-Algorithmus
Die Implementierung des Baum-Welch-Algorithmus beinhaltet normalerweise einige technische Details. Im Folgenden finden Sie einige Implementierungsdetails des Baum-Welch-Algorithmus:
1. Vermeiden Sie einen numerischen Unterlauf. Bei der Berechnung von α und β kann es aufgrund des geringen Wahrscheinlichkeitswerts zu einem numerischen Unterlauf kommen. Um dies zu vermeiden, können für Berechnungen die Funktionen Log-Probability und Log-Likelihood verwendet werden.
2. Vermeiden Sie eine Nullwahrscheinlichkeit
Bei der Berechnung von B kann es vorkommen, dass die Wahrscheinlichkeit, dass ein bestimmter Zustand zu einem bestimmten Zeitpunkt einen bestimmten Beobachtungswert erzeugt, Null ist. Um dies zu vermeiden, können Sie Glättungstechniken wie additive Glättung oder multiplikative Glättung verwenden.
3. Verwenden Sie mehrere Läufe
Da der Baum-Welch-Algorithmus zu einer lokalen optimalen Lösung konvergieren kann, ist es normalerweise erforderlich, den Algorithmus mehrmals auszuführen und die optimalen Modellparameter auszuwählen.
Im Allgemeinen ist der Baum-Welch-Algorithmus ein unbeaufsichtigter Lernalgorithmus, der auf dem EM-Algorithmus basiert und in der Verarbeitung natürlicher Sprache, der Spracherkennung und anderen Bereichen weit verbreitet ist.
Das obige ist der detaillierte Inhalt vonAnwendung des Baum-Welch-Algorithmus im impliziten Markov-Modell. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Wie fahre ich LLM lokal mit LM Studio aus? - Analytics VidhyaApr 19, 2025 am 11:38 AM
Wie fahre ich LLM lokal mit LM Studio aus? - Analytics VidhyaApr 19, 2025 am 11:38 AMMühelos großes Sprachmodelle zu Hause ausführen: LM Studio Benutzerhandbuch In den letzten Jahren haben Fortschritte in Software und Hardware es ermöglicht, große Sprachmodelle (LLMs) auf PCs durchzuführen. LM Studio ist ein hervorragendes Werkzeug, um diesen Prozess einfach und bequem zu machen. In diesem Artikel wird in LM Studio in LLM ausgelöst, wobei wichtige Schritte, mögliche Herausforderungen und die Vorteile von LLM vor Ort abdecken. Egal, ob Sie ein Technikbegeisterter sind oder neugierig auf die neuesten KI -Technologien sind, dieser Leitfaden bietet wertvolle Erkenntnisse und praktische Tipps. Fangen wir an! Überblick Verstehen Sie die grundlegenden Anforderungen für die lokale Ausführung von LLM. Richten Sie LM Studi auf Ihrem Computer ein
 Guy Peri hilft bei der Zukunft von McCormick durch DatenumwandlungApr 19, 2025 am 11:35 AM
Guy Peri hilft bei der Zukunft von McCormick durch DatenumwandlungApr 19, 2025 am 11:35 AMGuy Peri ist McCormicks Chief Information und Digital Officer. Obwohl Peri nur sieben Monate nach seiner Rolle eine umfassende Transformation der digitalen Fähigkeiten des Unternehmens vorantreibt. Sein beruflicher Fokus auf Daten und Analysen informiert
 Was ist die Kette von Emotionen in der schnellen Ingenieurwesen? - Analytics VidhyaApr 19, 2025 am 11:33 AM
Was ist die Kette von Emotionen in der schnellen Ingenieurwesen? - Analytics VidhyaApr 19, 2025 am 11:33 AMEinführung Künstliche Intelligenz (KI) entwickelt sich, um nicht nur Wörter, sondern auch Emotionen zu verstehen und mit einer menschlichen Berührung zu reagieren. Diese anspruchsvolle Interaktion ist im schnell vorrückenden Bereich der KI und der Verarbeitung natürlicher Sprache von entscheidender Bedeutung. Th
 12 Beste KI -Tools für den Datenwissenschafts -Workflow - Analytics VidhyaApr 19, 2025 am 11:31 AM
12 Beste KI -Tools für den Datenwissenschafts -Workflow - Analytics VidhyaApr 19, 2025 am 11:31 AMEinführung In der heutigen datenzentrierten Welt ist die Nutzung fortschrittlicher KI-Technologien für Unternehmen, die einen Wettbewerbsvorteil und eine verbesserte Effizienz suchen, von entscheidender Bedeutung. Eine Reihe leistungsstarker Tools ermöglichen Datenwissenschaftlern, Analysten und Entwicklern, aufzubauen, zu erschrecken
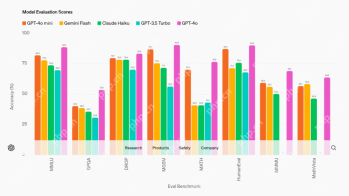 AV-Byte: OpenAIs GPT-4O-Mini und andere KI-InnovationenApr 19, 2025 am 11:30 AM
AV-Byte: OpenAIs GPT-4O-Mini und andere KI-InnovationenApr 19, 2025 am 11:30 AMDie KI -Landschaft dieser Woche explodierte mit bahnbrechenden Veröffentlichungen von Branchengiganten wie Openai, Mistral AI, Nvidia, Deepseek und Umarmungsgesicht. Diese neuen Modelle versprechen eine erhöhte Leistung, Erschwinglichkeit und Zugänglichkeit, die durch Fortschritte in TR angeheizt werden
 Die Android -App der Verwirrung ist mit Sicherheitsfehler befallen, BerichtsfundeApr 19, 2025 am 11:24 AM
Die Android -App der Verwirrung ist mit Sicherheitsfehler befallen, BerichtsfundeApr 19, 2025 am 11:24 AMDie Android -App des Unternehmens, die nicht nur Suchfunktionen bietet, sondern auch als KI -Assistent fungiert, ist jedoch mit einer Vielzahl von Sicherheitsproblemen, die seine Benutzer Datendiebstahl, Übernahmen und Identitätsangriffe von böswilligen Angriffen aussetzen könnten
 Jeder kann besser KI verwenden: Gedanken zur Stimmung codierenApr 19, 2025 am 11:17 AM
Jeder kann besser KI verwenden: Gedanken zur Stimmung codierenApr 19, 2025 am 11:17 AMSie können sich ansehen, was auf Konferenzen und Handelsshows passiert. Sie können Ingenieure fragen, was sie tun, oder sich mit einem CEO wenden. Überall, wo Sie aussehen, ändern sich die Dinge mit brezdemschneller Geschwindigkeit. Ingenieure und Nicht-Ingenieure Was ist der Unterschied?
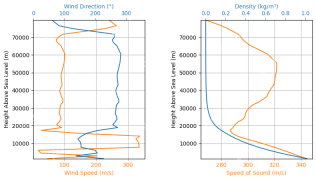 Raketenstartsimulation und -analyse unter Verwendung von Rocketpy - Analytics VidhyaApr 19, 2025 am 11:12 AM
Raketenstartsimulation und -analyse unter Verwendung von Rocketpy - Analytics VidhyaApr 19, 2025 am 11:12 AMSimulieren Raketenstarts mit Rocketpy: Eine umfassende Anleitung Dieser Artikel führt Sie durch die Simulation von Rocketpy-Starts mit hoher Leistung mit Rocketpy, einer leistungsstarken Python-Bibliothek. Wir werden alles abdecken, von der Definition von Raketenkomponenten bis zur Analyse von Simula


Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Dreamweaver Mac
Visuelle Webentwicklungstools

Herunterladen der Mac-Version des Atom-Editors
Der beliebteste Open-Source-Editor

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

MinGW – Minimalistisches GNU für Windows
Dieses Projekt wird derzeit auf osdn.net/projects/mingw migriert. Sie können uns dort weiterhin folgen. MinGW: Eine native Windows-Portierung der GNU Compiler Collection (GCC), frei verteilbare Importbibliotheken und Header-Dateien zum Erstellen nativer Windows-Anwendungen, einschließlich Erweiterungen der MSVC-Laufzeit zur Unterstützung der C99-Funktionalität. Die gesamte MinGW-Software kann auf 64-Bit-Windows-Plattformen ausgeführt werden.






