Die Prinzipien und Eigenschaften von Rot-Schwarz-Bäumen und ihre Code-Implementierung in Python

Der Rot-Schwarz-Baum ist wie der B+-Baum ein ausgeglichener binärer Suchbaum. Jeder Knoten eines rot-schwarzen Baumes ist gefärbt, entweder rot oder schwarz, aber die Wurzeln des Baumes sind schwarz und die Blätter an der Unterseite sind ebenfalls schwarz. Beachten Sie außerdem, dass der direkte Pfad von jedem Knoten zu einem Blatt in einem rot-schwarzen Baum die gleiche Anzahl schwarzer Knoten enthält.

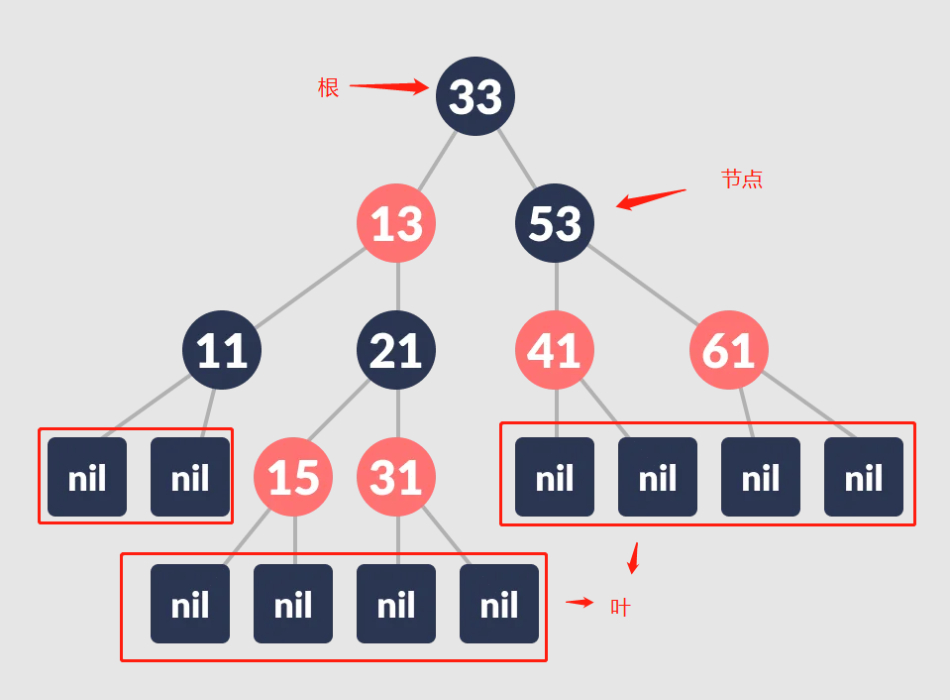
Wie bewahren rot-schwarze Bäume ihre selbstausgleichenden Eigenschaften?

Die Beschränkung der rot-schwarzen Baumknotenfarben stellt sicher, dass der längste Weg von der Wurzel zum Blatt nicht mehr als doppelt so groß ist wie der kürzeste Weg.

Warum sind neu eingefügte Knoten in rot-schwarzen Bäumen immer rot?

Das liegt daran, dass das Einfügen roter Knoten nicht gegen die Eigenschaft der Anzahl schwarzer Knoten rot-schwarzer Bäume verstößt. Und selbst wenn ein neuer roter Knoten in den ursprünglichen roten Knoten eingefügt wird, ist die Lösung dieses Problems einfacher als das Problem, das durch die Verletzung des schwarzen Knotens verursacht wird.

Rot-Schwarz-Baum-Python-Code-Implementierung

import sys
# 创建节点
class Node():
    def __init__(self, item):
        self.item = item
        self.parent = None
        self.left = None
        self.right = None
        self.color = 1

class RedBlackTree():
    def __init__(self):
        self.TNULL = Node(0)
        self.TNULL.color = 0
        self.TNULL.left = None
        self.TNULL.right = None
        self.root = self.TNULL

    # 前序
    def pre_order_helper(self, node):
        if node != TNULL:
            sys.stdout.write(node.item + " ")
            self.pre_order_helper(node.left)
            self.pre_order_helper(node.right)

    # 中序
    def in_order_helper(self, node):
        if node != TNULL:
            self.in_order_helper(node.left)
            sys.stdout.write(node.item + " ")
            self.in_order_helper(node.right)

# 后根
    def post_order_helper(self, node):
        if node != TNULL:
            self.post_order_helper(node.left)
            self.post_order_helper(node.right)
            sys.stdout.write(node.item + " ")

    # 搜索树
    def search_tree_helper(self, node, key):
        if node == TNULL or key == node.item:
            return node

        if key < node.item:
            return self.search_tree_helper(node.left, key)
        return self.search_tree_helper(node.right, key)

    # 删除后平衡树
    def delete_fix(self, x):
        while x != self.root and x.color == 0:
            if x == x.parent.left:
                s = x.parent.right
                if s.color == 1:
                    s.color = 0
                    x.parent.color = 1
                    self.left_rotate(x.parent)
                    s = x.parent.right

                if s.left.color == 0 and s.right.color == 0:
                    s.color = 1
                    x = x.parent
                else:
                    if s.right.color == 0:
                        s.left.color = 0
                        s.color = 1
                        self.right_rotate(s)
                        s = x.parent.right

                    s.color = x.parent.color
                    x.parent.color = 0
                    s.right.color = 0
                    self.left_rotate(x.parent)
                    x = self.root
            else:
                s = x.parent.left
                if s.color == 1:
                    s.color = 0
                    x.parent.color = 1
                    self.right_rotate(x.parent)
                    s = x.parent.left

                if s.right.color == 0 and s.right.color == 0:
                    s.color = 1
                    x = x.parent
                else:
                    if s.left.color == 0:
                        s.right.color = 0
                        s.color = 1
                        self.left_rotate(s)
                        s = x.parent.left

                    s.color = x.parent.color
                    x.parent.color = 0
                    s.left.color = 0
                    self.right_rotate(x.parent)
                    x = self.root
        x.color = 0

    def __rb_transplant(self, u, v):
        if u.parent == None:
            self.root = v
        elif u == u.parent.left:
            u.parent.left = v
        else:
            u.parent.right = v
        v.parent = u.parent

    # 节点删除
    def delete_node_helper(self, node, key):
        z = self.TNULL
        while node != self.TNULL:
            if node.item == key:
                z = node

            if node.item <= key:
                node = node.right
            else:
                node = node.left

        if z == self.TNULL:
            print("Cannot find key in the tree")
            return

        y = z
        y_original_color = y.color
        if z.left == self.TNULL:
            x = z.right
            self.__rb_transplant(z, z.right)
        elif (z.right == self.TNULL):
            x = z.left
            self.__rb_transplant(z, z.left)
        else:
            y = self.minimum(z.right)
            y_original_color = y.color
            x = y.right
            if y.parent == z:
                x.parent = y
            else:
                self.__rb_transplant(y, y.right)
                y.right = z.right
                y.right.parent = y

            self.__rb_transplant(z, y)
            y.left = z.left
            y.left.parent = y
            y.color = z.color
        if y_original_color == 0:
            self.delete_fix(x)

    # 插入后平衡树
    def fix_insert(self, k):
        while k.parent.color == 1:
            if k.parent == k.parent.parent.right:
                u = k.parent.parent.left
                if u.color == 1:
                    u.color = 0
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    k = k.parent.parent
                else:
                    if k == k.parent.left:
                        k = k.parent
                        self.right_rotate(k)
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    self.left_rotate(k.parent.parent)
            else:
                u = k.parent.parent.right

                if u.color == 1:
                    u.color = 0
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    k = k.parent.parent
                else:
                    if k == k.parent.right:
                        k = k.parent
                        self.left_rotate(k)
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    self.right_rotate(k.parent.parent)
            if k == self.root:
                break
        self.root.color = 0

    # Printing the tree
    def __print_helper(self, node, indent, last):
        if node != self.TNULL:
            sys.stdout.write(indent)
            if last:
                sys.stdout.write("R----")
                indent += "     "
            else:
                sys.stdout.write("L----")
                indent += "|    "

            s_color = "RED" if node.color == 1 else "BLACK"
            print(str(node.item) + "(" + s_color + ")")
            self.__print_helper(node.left, indent, False)
            self.__print_helper(node.right, indent, True)

    def preorder(self):
        self.pre_order_helper(self.root)

    def inorder(self):
        self.in_order_helper(self.root)

    def postorder(self):
        self.post_order_helper(self.root)

    def searchTree(self, k):
        return self.search_tree_helper(self.root, k)

    def minimum(self, node):
        while node.left != self.TNULL:
            node = node.left
        return node

    def maximum(self, node):
        while node.right != self.TNULL:
            node = node.right
        return node

    def successor(self, x):
        if x.right != self.TNULL:
            return self.minimum(x.right)

        y = x.parent
        while y != self.TNULL and x == y.right:
            x = y
            y = y.parent
        return y

    def predecessor(self,  x):
        if (x.left != self.TNULL):
            return self.maximum(x.left)

        y = x.parent
        while y != self.TNULL and x == y.left:
            x = y
            y = y.parent

        return y

    def left_rotate(self, x):
        y = x.right
        x.right = y.left
        if y.left != self.TNULL:
            y.left.parent = x

        y.parent = x.parent
        if x.parent == None:
            self.root = y
        elif x == x.parent.left:
            x.parent.left = y
        else:
            x.parent.right = y
        y.left = x
        x.parent = y

    def right_rotate(self, x):
        y = x.left
        x.left = y.right
        if y.right != self.TNULL:
            y.right.parent = x

        y.parent = x.parent
        if x.parent == None:
            self.root = y
        elif x == x.parent.right:
            x.parent.right = y
        else:
            x.parent.left = y
        y.right = x
        x.parent = y

    def insert(self, key):
        node = Node(key)
        node.parent = None
        node.item = key
        node.left = self.TNULL
        node.right = self.TNULL
        node.color = 1

        y = None
        x = self.root

        while x != self.TNULL:
            y = x
            if node.item < x.item:
                x = x.left
            else:
                x = x.right

        node.parent = y
        if y == None:
            self.root = node
        elif node.item < y.item:
            y.left = node
        else:
            y.right = node

        if node.parent == None:
            node.color = 0
            return

        if node.parent.parent == None:
            return

        self.fix_insert(node)

    def get_root(self):
        return self.root

    def delete_node(self, item):
        self.delete_node_helper(self.root, item)

    def print_tree(self):
        self.__print_helper(self.root, "", True)


if __name__ == "__main__":
    bst = RedBlackTree()

    bst.insert(55)
    bst.insert(40)
    bst.insert(65)
    bst.insert(60)
    bst.insert(75)
    bst.insert(57)

    bst.print_tree()

    print("\nAfter deleting an element")
    bst.delete_node(40)
    bst.print_tree()

Das obige ist der detaillierte Inhalt vonDie Prinzipien und Eigenschaften von Rot-Schwarz-Bäumen und ihre Code-Implementierung in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!