Heim >Technologie-Peripheriegeräte >KI >Eingehende Analyse der Konzepte und Anwendungen mehrerer linearer Regressionsmodelle
Eingehende Analyse der Konzepte und Anwendungen mehrerer linearer Regressionsmodelle
- 王林nach vorne
- 2024-01-22 18:30:211699Durchsuche
Multiple lineare Regression ist die häufigste Form der linearen Regression und wird verwendet, um zu beschreiben, wie eine einzelne Antwortvariable Y eine lineare Beziehung zu mehreren Prädiktorvariablen aufweist.
Beispiele für Anwendungen, bei denen die multiple Regression verwendet werden kann:
Der Verkaufspreis eines Hauses kann durch Faktoren wie Lage, Anzahl der Schlafzimmer und Badezimmer, Baujahr, Grundstücksgröße usw. beeinflusst werden.
2. Die Größe eines Kindes hängt von der Größe der Mutter, der Größe des Vaters, der Ernährung und Umweltfaktoren ab.
Parameter des multiplen linearen Regressionsmodells
Betrachten Sie ein multiples lineares Regressionsmodell mit k unabhängigen Prädiktorvariablen x1, x2..., xk und einer Antwortvariablen y.
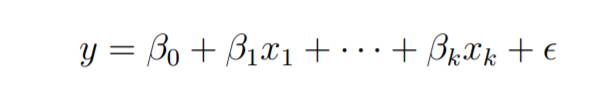
Angenommen, wir haben n Beobachtungen für k+1 Variablen und n Variablen sollten größer als k sein.
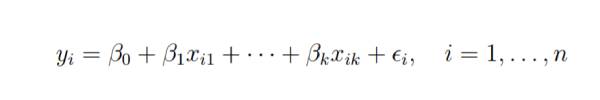
Das grundlegende Ziel der Regression der kleinsten Quadrate besteht darin, die Hyperebene in den (k+1)-dimensionalen Raum einzupassen, um die Summe der quadrierten Residuen zu minimieren.
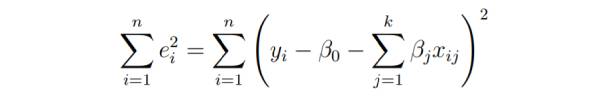
Bevor Sie die Modellparameter differenzieren, setzen Sie sie auf Null und leiten Sie die Normalgleichung der kleinsten Quadrate ab, die die Parameter erfüllen müssen.
Diese Gleichungen werden mit Hilfe von Vektoren und Matrizen formuliert.

Ein lineares Regressionsmodell wird wie folgt geschrieben:
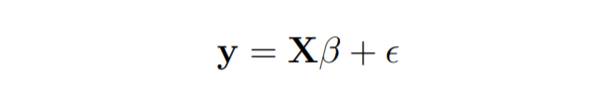
Bei der linearen Regression schätzt der Parameter der kleinsten Quadrate b
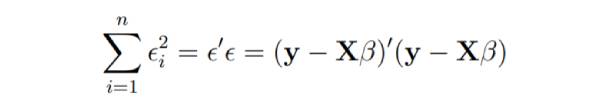
Stellen Sie sich vor, dass die Daten der Problem , und sagen wir, b ist variabel. Wir möchten das „beste“ b finden, das die Summe der quadrierten Residuen minimiert.
Die kleinstmögliche Quadratsumme ist Null.
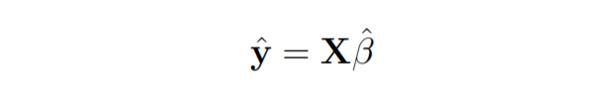
Hier ist y der geschätzte Antwortvektor.
Der Code implementiert eine mehrfache lineare Regression für den Datensatz data2
data2-Datensatz
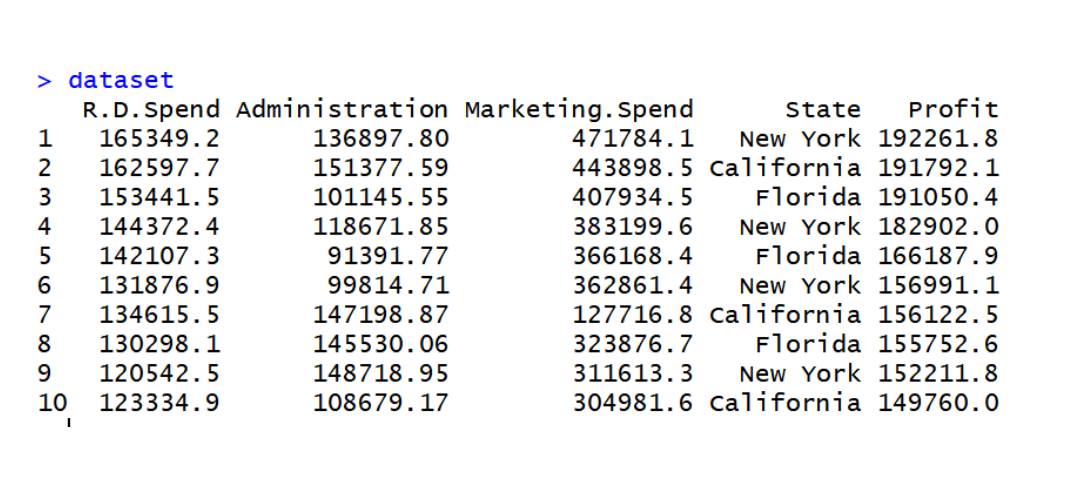
dataset=read.csv('data2.csv') dataset$State=factor(dataset$State, levels=c('New York','California','Florida'), labels=c(1,2,3)) dataset$State
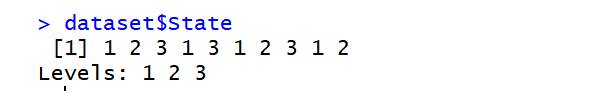
library(caTools) set.seed(123) split=sample.split(dataset$Profit,SplitRatio=0.8) training_set=subset(dataset,split==TRUE) test_set=subset(dataset,split==FALSE) regressor=lm(formula=Profit~., data=training_set) y_pred=predict(regressor,newdata=test_set)
Das obige ist der detaillierte Inhalt vonEingehende Analyse der Konzepte und Anwendungen mehrerer linearer Regressionsmodelle. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

