Detaillierte Erläuterung der Schritte zur Implementierung mehrerer linearer Regressionssimulationskurvenalgorithmen in PHP

Dieses Mal werde ich Ihnen die Schritte zum Implementieren des Simulationskurvenalgorithmus für mehrere lineare Regressionen in PHP ausführlich erläutern ist ein praktischer Fall, werfen wir einen Blick darauf. Multiples lineares Regressionsmodell:

y = b1x1 + b2x2 + b3x3 +... +bnxn;

Wir basieren auf einem Datensatz: ähnlich wie

arr_x = [[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [11, 12, 13, 14, 15]]; ;

Was wir schließlich finden wollen, ist ein Array, einschließlich von b1 bis bn; Methode: Verwenden Sie die Methode der kleinsten Quadrate

Formel:

Wir verwenden nur die erste Hälfte der Formel, das heißt, verwenden Sie eine Matrix zur Berechnung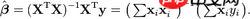

X in der Formel ist arr_x,

zweidimensionales Array

wir können es uns als Matrix vorstellen, y in der Formel ist arr_y, stellen Sie es sich auch als eine Matrix (5, 10, 15) vor, aber es sollte vertikal geschrieben werden. Dann werden wir gemäß der Formel feststellen, dass wir Matrixmultiplikation, Transposition und Inversion verwenden müssen, sodass die folgenden Codes nacheinander angegeben werden:

public function get_complement($data, $i, $j) {
  /* x和y为矩阵data的行数和列数 */
  $x = count($data);
  $y = count($data[0]);
  /* data2为所求剩余矩阵 */
  $data2 =[];
  for ($k = 0; $k < $x -1; $k++) {
    if ($k < $i) {
      for ($kk = 0; $kk < $y -1; $kk++) {
        if ($kk < $j) {
          $data2[$k][$kk] = $data[$k][$kk];
        } else {
          $data2[$k][$kk] = $data[$k][$kk +1];
        }
      }
    } else {
      for ($kk = 0; $kk < $y -1; $kk++) {
        if ($kk < $j) {
          $data2[$k][$kk] = $data[$k +1][$kk];
        } else {
          $data2[$k][$kk] = $data[$k +1][$kk +1];
        }
      }
    }
  }
  return $data2;
}
/* 计算矩阵行列式 */
public function cal_det($data) {
  $ans = 0;
  if (count($data[0]) === 2) {
    $ans = $data[0][0] * $data[1][1] - $data[0][1] * $data[1][0];
  } else {
    for ($i = 0; $i < count($data[0]); $i++) {
      $data_temp = $this->get_complement($data, 0, $i);
      if ($i % 2 === 0) {
        $ans = $ans + $data[0][$i] * ($this->cal_det($data_temp));
      } else {
        $ans = $ans - $data[0][$i] * ($this->cal_det($data_temp));
      }
    }
  }
  return $ans;
}
/*计算矩阵的伴随矩阵*/
public function ajoint($data) {
  $m = count($data);
  $n = count($data[0]);
  $data2 =[];
  for ($i = 0; $i < $m; $i++) {
    for ($j = 0; $j < $n; $j++) {
      if (($i + $j) % 2 === 0) {
        $data2[$i][$j] = $this->cal_det($this->get_complement($data, $i, $j));
      } else {
        $data2[$i][$j] = - $this->cal_det($this->get_complement($data, $i, $j));
      }
    }
  }
  return $this->trans($data2);
}
/*转置矩阵*/
public function trans($data) {
  $i = count($data);
  $j = count($data[0]);
  $data2 =[];
  for ($k2 = 0; $k2 < $j; $k2++) {
    for ($k1 = 0; $k1 < $i; $k1++) {
      $data2[$k2][$k1] = $data[$k1][$k2];
    }
  }
  /*将矩阵转置便可得到伴随矩阵*/
  return $data2;
}
/*求矩阵的逆，输入参数为原矩阵*/
public function inv($data) {
  $m = count($data);
  $n = count($data[0]);
  $data2 =[];
  $det_val = $this->cal_det($data);
  $data2 = $this->ajoint($data);
  for ($i = 0; $i < $m; $i++) {
    for ($j = 0; $j < $n; $j++) {
      $data2[$i][$j] = $data2[$i][$j] / $det_val;
    }
  }
  return $data2;
}
/*求两矩阵的乘积*/
public function getProduct($data1, $data2) {
  /*$data1 为左乘矩阵*/
  $m1 = count($data1);
  $n1 = count($data1[0]);
  $m2 = count($data2);
  $n2 = count($data2[0]);
  $data_new =[];
  if ($n1 !== $m2) {
    return false;
  } else {
    for ($i = 0; $i <= $m1 -1; $i++) {
      for ($k = 0; $k <= $n2 -1; $k++) {
        $data_new[$i][$k] = 0;
        for ($j = 0; $j <= $n1 -1; $j++) {
          $data_new[$i][$k] += $data1[$i][$j] * $data2[$j][$k];
        }
      }
    }
  }
  return $data_new;
}
/*多元线性方程*/
public function getParams($arr_x, $arr_y) {
  $final =[];
  $arr_x_t = $this->trans($arr_x);
  $result = $this->getProduct($this->getProduct($this->inv($this->getProduct($arr_x_t, $arr_x)), $arr_x_t), $arr_y);
  foreach ($result as $key => $val) {
    foreach ($val as $_k => $_v) {
      $final[] = $_v;
    }
  }
  return $final;
}

Das Finale

Die Methode lautet schließlich: Um das b-Parameter-Array zu finden, übergeben Sie einfach ein zweidimensionales Array arr_x und ein

eindimensionales Array getParams()arr_y. Ich glaube, dass Sie die Methode beherrschen, nachdem Sie den Fall in diesem Artikel gelesen haben. Weitere spannende Informationen finden Sie in anderen verwandten Artikeln auf der chinesischen PHP-Website!

Empfohlene Lektüre:

Detaillierte Erklärung der Schritte zum Konvertieren eines Arrays mit foreach in PHP

Detaillierte Erklärung der Schritte zum Löschen von Wertelementen in einem eindimensionalen Array in PHP

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung der Schritte zur Implementierung mehrerer linearer Regressionssimulationskurvenalgorithmen in PHP. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!