Heim >Technologie-Peripheriegeräte >KI >Implementierung des Mixed Expert Model (MoE) mit PyTorch
Implementierung des Mixed Expert Model (MoE) mit PyTorch
- 王林nach vorne
- 2024-01-16 08:42:16627Durchsuche
Die Einführung von Mixtral 8x7B hat im Bereich der offenen KI große Aufmerksamkeit erregt, insbesondere das Konzept der Mixture-of-Experts (MoEs), das jedem bekannt ist. Das Hybrid Expertise (MoE)-Konzept symbolisiert kollaborative Intelligenz und verkörpert die Idee, dass das Ganze größer ist als die Summe seiner Teile. Das MoE-Modell integriert die Vorteile mehrerer Expertenmodelle, um genauere Vorhersagen zu ermöglichen. Es besteht aus einem geschlossenen Netzwerk und einer Reihe von Expertennetzwerken, von denen jedes gut darin ist, verschiedene Aspekte einer bestimmten Aufgabe zu bewältigen. Durch die richtige Zuweisung von Aufgaben und Gewichtungen kann das MoE-Modell das Fachwissen von Experten nutzen und so die Gesamtvorhersageleistung verbessern. Dieses kollaborative intelligente Modell hat neue Durchbrüche in der Entwicklung des KI-Bereichs gebracht und wird in zukünftigen Anwendungen eine wichtige Rolle spielen.
In diesem Artikel wird PyTorch zur Implementierung des MoE-Modells verwendet. Bevor wir den spezifischen Code vorstellen, stellen wir kurz die Architektur des Hybridexperten vor.
MoE-Architektur
MoE besteht aus zwei Arten von Netzwerken: (1) Expertennetzwerk und (2) Gated Network.
Expert Network ist eine Methode, die ein proprietäres Modell verwendet, das bei einer Teilmenge der Daten eine gute Leistung erbringt. Sein Kernkonzept besteht darin, den Problemraum durch mehrere Experten mit komplementären Stärken abzudecken, um eine umfassende Lösung des Problems sicherzustellen. Jedes Expertenmodell wird mit einzigartigen Fähigkeiten und Erfahrungen geschult, wodurch die Gesamtleistung und -effektivität des Systems verbessert wird. Durch den Einsatz von Expertennetzwerken können komplexe Aufgaben und Bedürfnisse effektiv angegangen und bessere Lösungen bereitgestellt werden.
Ein geschlossenes Netzwerk ist ein Netzwerk, das dazu dient, die Beiträge von Experten zu leiten, zu koordinieren oder zu verwalten. Es bestimmt, welches Netzwerk eine bestimmte Eingabe am besten verarbeiten kann, indem es die Fähigkeiten verschiedener Netzwerke für verschiedene Arten von Eingaben lernt und abwägt. Ein gut ausgebildetes Gating-Netzwerk kann neue Eingabevektoren bewerten und Verarbeitungsaufgaben je nach Kompetenz dem am besten geeigneten Experten oder der am besten geeigneten Expertenkombination zuweisen. Das Gating-Netzwerk passt die Gewichtungen dynamisch an, basierend auf der Relevanz der Expertenausgabe für die aktuelle Eingabe, um personalisierte Antworten zu gewährleisten. Dieser Mechanismus zur dynamischen Anpassung der Gewichte ermöglicht es dem Gating-Netzwerk, sich flexibel an unterschiedliche Situationen und Bedürfnisse anzupassen.
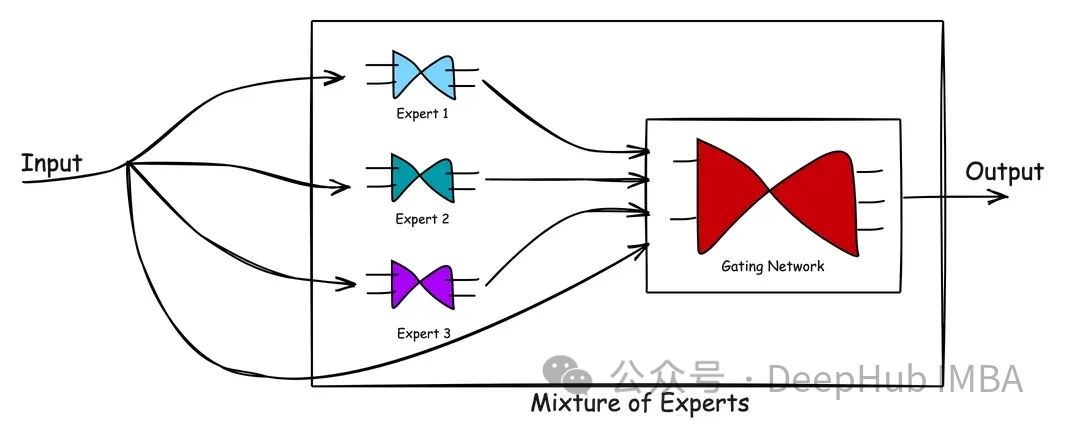
Das obige Bild zeigt den Verarbeitungsablauf in MoE. Der Vorteil des gemischten Expertenmodells ist seine Einfachheit. Durch das Erlernen des komplexen Problemraums und der Reaktionen von Experten bei der Lösung des Problems tragen MoE-Modelle dazu bei, bessere Lösungen zu erzielen als ein einzelner Experte. Das Gating-Netzwerk fungiert als effektiver Manager, der Szenarien bewertet und Aufgaben an die besten Experten weitergibt. Wenn neue Daten eingegeben werden, kann sich das Modell anpassen, indem es die Stärken des Experten anhand der neuen Eingabe neu bewertet, was zu einem flexiblen Lernansatz führt. Kurz gesagt: Das MoE-Modell nutzt das Wissen und die Erfahrung mehrerer Experten, um komplexe Probleme zu lösen. Durch die Verwaltung eines geschlossenen Netzwerks kann das Modell die am besten geeigneten Experten für die Bearbeitung von Aufgaben entsprechend verschiedenen Szenarien auswählen. Die Vorteile dieses Ansatzes liegen darin, dass er bessere Lösungen als ein einzelner Experte liefern kann und sich flexibel an neue Eingabedaten anpassen lässt. Insgesamt handelt es sich beim MoE-Modell um eine effektive und einfache Methode, mit der sich eine Vielzahl komplexer Probleme lösen lassen.
MoE bietet enorme Vorteile für die Bereitstellung von Modellen für maschinelles Lernen. Hier sind zwei bemerkenswerte Vorteile. Die Kernstärke von
MoE liegt in seinem vielfältigen und professionellen Expertennetzwerk. Durch die Einstellung von MoE können Probleme in mehreren Bereichen mit hoher Genauigkeit behandelt werden, was mit einem einzelnen Modell nur schwer zu erreichen ist.
MoE ist von Natur aus skalierbar. Mit zunehmender Aufgabenkomplexität können mehr Experten nahtlos in das System integriert werden, wodurch der Umfang des Fachwissens erweitert wird, ohne dass andere Expertenmodelle geändert werden müssen. Mit anderen Worten: MoE kann vorab geschulte Experten in maschinelle Lernsysteme integrieren, um die Systeme bei der Bewältigung wachsender Aufgabenanforderungen zu unterstützen.
Gemischte Expertenmodelle finden in vielen Bereichen Anwendung, darunter Empfehlungssysteme, Sprachmodellierung und verschiedene komplexe Vorhersageaufgaben. Es gibt Gerüchte, dass GPT-4 aus mehreren Experten besteht. Obwohl wir dies nicht bestätigen können, liefert ein Modell wie gpt-4 die besten Ergebnisse, indem es die Leistung mehrerer Modelle durch den MoE-Ansatz nutzt.
Pytorch-Code
Wir werden hier nicht auf die MOE-Technologie eingehen, die in großen Modellen wie Mixtral 8x7B verwendet wird. Stattdessen schreiben wir ein einfaches benutzerdefiniertes MOE, das auf jede Aufgabe angewendet werden kann Code Das Funktionsprinzip von MOE ist sehr hilfreich, um zu verstehen, wie MOE in großen Modellen funktioniert.
Im Folgenden stellen wir die Code-Implementierung von PyTorch Stück für Stück vor.
Bibliothek importieren:
import torch import torch.nn as nn import torch.optim as optim
Expertenmodell definieren:
class Expert(nn.Module): def __init__(self, input_dim, hidden_dim, output_dim): super(Expert, self).__init__() self.layer1 = nn.Linear(input_dim, hidden_dim) self.layer2 = nn.Linear(hidden_dim, output_dim) def forward(self, x): x = torch.relu(self.layer1(x)) return torch.softmax(self.layer2(x), dim=1)
Hier definieren wir ein einfaches Expertenmodell. Sie können sehen, dass es sich um ein zweischichtiges MLP handelt, das Relu-Aktivierung verwendet und schließlich Softmax-Ausgaben verwendet die Klassifizierungswahrscheinlichkeit.
Gating-Modell definieren:
# Define the gating model class Gating(nn.Module): def __init__(self, input_dim,num_experts, dropout_rate=0.1): super(Gating, self).__init__() # Layers self.layer1 = nn.Linear(input_dim, 128) self.dropout1 = nn.Dropout(dropout_rate) self.layer2 = nn.Linear(128, 256) self.leaky_relu1 = nn.LeakyReLU() self.dropout2 = nn.Dropout(dropout_rate) self.layer3 = nn.Linear(256, 128) self.leaky_relu2 = nn.LeakyReLU() self.dropout3 = nn.Dropout(dropout_rate) self.layer4 = nn.Linear(128, num_experts) def forward(self, x): x = torch.relu(self.layer1(x)) x = self.dropout1(x) x = self.layer2(x) x = self.leaky_relu1(x) x = self.dropout2(x) x = self.layer3(x) x = self.leaky_relu2(x) x = self.dropout3(x) return torch.softmax(self.layer4(x), dim=1)
门控模型更复杂,有三个线性层和dropout层用于正则化以防止过拟合。它使用ReLU和LeakyReLU激活函数引入非线性。最后一层的输出大小等于专家的数量,并对这些输出应用softmax函数。输出权重,这样可以将专家的输出与之结合。
说明:其实门控网络,或者叫路由网络是MOE中最复杂的部分,因为它涉及到控制输入到那个专家模型,所以门控网络也有很多个设计方案,例如(如果我没记错的话)Mixtral 8x7B 只是取了8个专家中的top2。所以我们这里不详细讨论各种方案,只是介绍其基本原理和代码实现。
完整的MOE模型:
class MoE(nn.Module): def __init__(self, trained_experts): super(MoE, self).__init__() self.experts = nn.ModuleList(trained_experts) num_experts = len(trained_experts) # Assuming all experts have the same input dimension input_dim = trained_experts[0].layer1.in_features self.gating = Gating(input_dim, num_experts) def forward(self, x): # Get the weights from the gating network weights = self.gating(x) # Calculate the expert outputs outputs = torch.stack([expert(x) for expert in self.experts], dim=2) # Adjust the weights tensor shape to match the expert outputs weights = weights.unsqueeze(1).expand_as(outputs) # Multiply the expert outputs with the weights and # sum along the third dimension return torch.sum(outputs * weights, dim=2)
这里主要看前向传播的代码,通过输入计算出权重和每个专家给出输出的预测,最后使用权重将所有专家的结果求和最终得到模型的输出。
这个是不是有点像“集成学习”。
测试
下面我们来对我们的实现做个简单的测试,首先生成一个简单的数据集:
# Generate the dataset num_samples = 5000 input_dim = 4 hidden_dim = 32 # Generate equal numbers of labels 0, 1, and 2 y_data = torch.cat([ torch.zeros(num_samples // 3), torch.ones(num_samples // 3), torch.full((num_samples - 2 * (num_samples // 3),), 2)# Filling the remaining to ensure exact num_samples ]).long() # Biasing the data based on the labels x_data = torch.randn(num_samples, input_dim) for i in range(num_samples): if y_data[i] == 0: x_data[i, 0] += 1# Making x[0] more positive elif y_data[i] == 1: x_data[i, 1] -= 1# Making x[1] more negative elif y_data[i] == 2: x_data[i, 0] -= 1# Making x[0] more negative # Shuffle the data to randomize the order indices = torch.randperm(num_samples) x_data = x_data[indices] y_data = y_data[indices] # Verify the label distribution y_data.bincount() # Shuffle the data to ensure x_data and y_data remain aligned shuffled_indices = torch.randperm(num_samples) x_data = x_data[shuffled_indices] y_data = y_data[shuffled_indices] # Splitting data for training individual experts # Use the first half samples for training individual experts x_train_experts = x_data[:int(num_samples/2)] y_train_experts = y_data[:int(num_samples/2)] mask_expert1 = (y_train_experts == 0) | (y_train_experts == 1) mask_expert2 = (y_train_experts == 1) | (y_train_experts == 2) mask_expert3 = (y_train_experts == 0) | (y_train_experts == 2) # Select an almost equal number of samples for each expert num_samples_per_expert = \ min(mask_expert1.sum(), mask_expert2.sum(), mask_expert3.sum()) x_expert1 = x_train_experts[mask_expert1][:num_samples_per_expert] y_expert1 = y_train_experts[mask_expert1][:num_samples_per_expert] x_expert2 = x_train_experts[mask_expert2][:num_samples_per_expert] y_expert2 = y_train_experts[mask_expert2][:num_samples_per_expert] x_expert3 = x_train_experts[mask_expert3][:num_samples_per_expert] y_expert3 = y_train_experts[mask_expert3][:num_samples_per_expert] # Splitting the next half samples for training MoE model and for testing x_remaining = x_data[int(num_samples/2)+1:] y_remaining = y_data[int(num_samples/2)+1:] split = int(0.8 * len(x_remaining)) x_train_moe = x_remaining[:split] y_train_moe = y_remaining[:split] x_test = x_remaining[split:] y_test = y_remaining[split:] print(x_train_moe.shape,"\n", x_test.shape,"\n", x_expert1.shape,"\n", x_expert2.shape,"\n", x_expert3.shape)
这段代码创建了一个合成数据集,其中包含三个类标签——0、1和2。基于类标签对特征进行操作,从而在数据中引入一些模型可以学习的结构。
数据被分成针对个别专家的训练集、MoE模型和测试集。我们确保专家模型是在一个子集上训练的,这样第一个专家在标签0和1上得到很好的训练,第二个专家在标签1和2上得到更好的训练,第三个专家看到更多的标签2和0。
我们期望的结果是:虽然每个专家对标签0、1和2的分类准确率都不令人满意,但通过结合三位专家的决策,MoE将表现出色。
模型初始化和训练设置:
# Define hidden dimension output_dim = 3 hidden_dim = 32 epochs = 500 learning_rate = 0.001 # Instantiate the experts expert1 = Expert(input_dim, hidden_dim, output_dim) expert2 = Expert(input_dim, hidden_dim, output_dim) expert3 = Expert(input_dim, hidden_dim, output_dim) # Set up loss criterion = nn.CrossEntropyLoss() # Optimizers for experts optimizer_expert1 = optim.Adam(expert1.parameters(), lr=learning_rate) optimizer_expert2 = optim.Adam(expert2.parameters(), lr=learning_rate) optimizer_expert3 = optim.Adam(expert3.parameters(), lr=learning_rate)
实例化了专家模型和MoE模型。定义损失函数来计算训练损失,并为每个模型设置优化器,在训练过程中执行权重更新。
训练的步骤也非常简单
# Training loop for expert 1 for epoch in range(epochs):optimizer_expert1.zero_grad()outputs_expert1 = expert1(x_expert1)loss_expert1 = criterion(outputs_expert1, y_expert1)loss_expert1.backward()optimizer_expert1.step() # Training loop for expert 2 for epoch in range(epochs):optimizer_expert2.zero_grad()outputs_expert2 = expert2(x_expert2)loss_expert2 = criterion(outputs_expert2, y_expert2)loss_expert2.backward()optimizer_expert2.step() # Training loop for expert 3 for epoch in range(epochs):optimizer_expert3.zero_grad()outputs_expert3 = expert3(x_expert3)loss_expert3 = criterion(outputs_expert3, y_expert3)loss_expert3.backward()
每个专家使用基本的训练循环在不同的数据子集上进行单独的训练。循环迭代指定数量的epoch。
下面是我们MOE的训练
# Create the MoE model with the trained experts moe_model = MoE([expert1, expert2, expert3]) # Train the MoE model optimizer_moe = optim.Adam(moe_model.parameters(), lr=learning_rate) for epoch in range(epochs):optimizer_moe.zero_grad()outputs_moe = moe_model(x_train_moe)loss_moe = criterion(outputs_moe, y_train_moe)loss_moe.backward()optimizer_moe.step()
MoE模型是由先前训练过的专家创建的,然后在单独的数据集上进行训练。训练过程类似于单个专家的训练,但现在门控网络的权值在训练过程中更新。
最后我们的评估函数:
# Evaluate all models def evaluate(model, x, y):with torch.no_grad():outputs = model(x)_, predicted = torch.max(outputs, 1)correct = (predicted == y).sum().item()accuracy = correct / len(y)return accuracy
evaluate函数计算模型在给定数据上的精度(x代表样本,y代表预期标签)。准确度计算为正确预测数与预测总数之比。
结果如下:
accuracy_expert1 = evaluate(expert1, x_test, y_test) accuracy_expert2 = evaluate(expert2, x_test, y_test) accuracy_expert3 = evaluate(expert3, x_test, y_test) accuracy_moe = evaluate(moe_model, x_test, y_test) print("Expert 1 Accuracy:", accuracy_expert1) print("Expert 2 Accuracy:", accuracy_expert2) print("Expert 3 Accuracy:", accuracy_expert3) print("Mixture of Experts Accuracy:", accuracy_moe) #Expert 1 Accuracy: 0.466 #Expert 2 Accuracy: 0.496 #Expert 3 Accuracy: 0.378 #Mixture of Experts Accuracy: 0.614
可以看到
专家1正确预测了测试数据集中大约46.6%的样本的类标签。
专家2表现稍好,正确预测率约为49.6%。
专家3在三位专家中准确率最低,正确预测的样本约为37.8%。
而MoE模型显著优于每个专家,总体准确率约为61.4%。
总结
我们测试的输出结果显示了混合专家模型的强大功能。该模型通过门控网络将各个专家模型的优势结合起来,取得了比单个专家模型更高的精度。门控网络有效地学习了如何根据输入数据权衡每个专家的贡献,以产生更准确的预测。混合专家利用了各个模型的不同专业知识,在测试数据集上提供了更好的性能。
同时也说明我们可以在现有的任务上尝试使用MOE来进行测试,也可以得到更好的结果。
Das obige ist der detaillierte Inhalt vonImplementierung des Mixed Expert Model (MoE) mit PyTorch. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

