Implementierung eines Rauschentfernungs-Diffusionsmodells mit PyTorch

Bevor wir das Funktionsprinzip des Denoising Diffusion Probabilistic Model (DDPM) im Detail verstehen, wollen wir zunächst einige Aspekte der Entwicklung der generativen künstlichen Intelligenz verstehen, die auch zur Grundlagenforschung von DDPM gehört.

VAE

VAE verwendet einen Encoder, einen probabilistischen latenten Raum und einen Decoder. Während des Trainings sagt der Encoder den Mittelwert und die Varianz jedes Bildes voraus und tastet diese Werte aus einer Gaußschen Verteilung ab. Das Ergebnis der Abtastung wird an den Decoder weitergeleitet, der das Eingabebild in eine dem Ausgabebild ähnliche Form umwandelt. Zur Berechnung des Verlusts wird die KL-Divergenz verwendet. Ein wesentlicher Vorteil von VAE ist die Fähigkeit, vielfältige Bilder zu erzeugen. In der Abtastphase kann man direkt aus der Gaußschen Verteilung Stichproben ziehen und über den Decoder neue Bilder erzeugen.

GAN

Nur ein Jahr nach Variational Autoencoders (VAEs) entstand eine bahnbrechende Familie generativer Modelle – Generative Adversarial Networks (GANs), die eine neue Klasse generativer Modelle markierten. Der Beginn des Modells, gekennzeichnet durch die Die Zusammenarbeit zweier neuronaler Netze: eines Generators und eines Diskriminators, beinhaltet einen kontradiktorischen Trainingsprozess. Das Ziel des Generators besteht darin, aus zufälligem Rauschen reale Daten, beispielsweise Bilder, zu generieren, während der Diskriminator danach strebt, reale Daten von generierten Daten zu unterscheiden. Während der Trainingsphase verbessern der Generator und der Diskriminator kontinuierlich ihre Fähigkeiten durch einen wettbewerbsorientierten Lernprozess. Der Generator generiert immer überzeugendere Daten und wird dadurch intelligenter als der Diskriminator, was wiederum seine Fähigkeit verbessert, zwischen realen und generierten Proben zu unterscheiden. Dieses kontroverse Zusammenspiel gipfelt darin, dass der Generator hochwertige, realistische Daten produziert. In der Sampling-Phase, nach dem GAN-Training, generiert der Generator neue Samples durch Eingabe von Zufallsrauschen. Es wandelt dieses Rauschen in Daten um, die im Allgemeinen reale Beispiele widerspiegeln.

Warum wir eine andere Modellarchitektur brauchen

Obwohl GANs und VAEs jeweils ihre eigenen Vorteile bei der Bilderzeugung haben, haben sie beide einige Probleme. GANs können realistische Bilder erzeugen, die den Bildern im Trainingssatz sehr ähnlich sind, ihren generierten Ergebnissen mangelt es jedoch an Diversität. VAEs können eine Vielzahl von Bildern erzeugen, neigen jedoch dazu, verschwommene Bilder zu erzeugen. Es ist jedoch nicht gelungen, diese beiden Fähigkeiten zu kombinieren, um Bilder zu erstellen, die sowohl äußerst realistisch als auch vielfältig sind. Diese Herausforderung stellt ein erhebliches Hindernis für Forscher dar und muss angegangen werden. Daher besteht eine der zukünftigen Forschungsrichtungen darin, zu untersuchen, wie die Vorteile von GANs und VAEs kombiniert werden können, um eine äußerst realistische und vielfältige Bilderzeugung zu erreichen. Dies wird einen großen Durchbruch auf dem Gebiet der Bilderzeugung bringen und in verschiedenen Bereichen weit verbreitet sein.

Sechs Jahre nach Veröffentlichung des GAN-Papiers und sieben Jahre nach Veröffentlichung des VAE-Papiers entstand ein bahnbrechendes Modell, nämlich das Denoising Diffusion Probabilistic Model (DDPM). DDPM vereint die Vorteile beider Bereiche, um vielfältige und realistische Bilder zu erstellen.

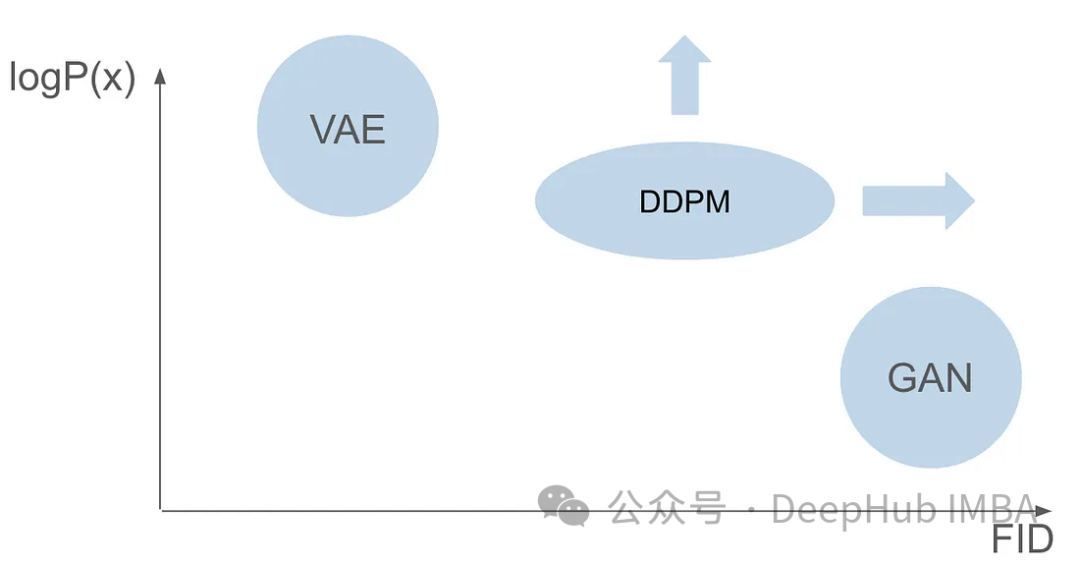
In diesem Artikel wird die Komplexität von DDPM im Detail untersucht, einschließlich des Trainingsprozesses, der Vorwärts- und Rückwärtsprozesse sowie der Stichprobenmethoden. Wir werden PyTorch verwenden, um DDPM von Grund auf zu erstellen und zu trainieren und die Leser durch den gesamten Prozess zu führen.

Es wird davon ausgegangen, dass Sie bereits mit den Grundlagen des Deep Learning vertraut sind und über solide Grundlagen in Deep Computer Vision verfügen. Wir werden nicht im Detail auf diese Grundkonzepte eingehen, sondern versuchen, Bilder zu generieren, die in ihrer Authentizität glaubwürdig sind.

DDPM

Denoising Diffusion Probabilistic Model (DDPM) ist eine hochmoderne Methode im Bereich generativer Modelle. Im Vergleich zu herkömmlichen Modellen, die auf expliziten Wahrscheinlichkeitsfunktionen basieren, arbeitet DDPM mit einem iterativen Entrauschungsdiffusionsprozess. Bei diesem Vorgang wird einem Bild schrittweise Rauschen hinzugefügt und versucht, dieses Rauschen zu entfernen. Die grundlegende Theorie basiert auf der Idee, eine einfache Verteilung (z. B. eine Gaußsche Verteilung) durch eine Reihe von Diffusionsschritten in eine komplexe und ausdrucksstarke Bilddatenverteilung umzuwandeln. Mit anderen Worten: Durch die Übertragung von Stichproben aus der ursprünglichen Bildverteilung in eine Gaußsche Verteilung können wir ein Modell erstellen, um diesen Prozess umzukehren. Dies ermöglicht es uns, von einer vollständig Gaußschen Verteilung auszugehen und neue Bilder mit Bildverteilungseigenschaften zu erzeugen, wodurch eine effiziente Bilderzeugung erreicht wird.

Das Training von DDPM besteht aus zwei grundlegenden Schritten: einem Vorwärtsprozess, der verrauschte Bilder erzeugt, die fest und nicht lernbar sind, und einem anschließenden Rückwärtsprozess. Das Hauptziel des umgekehrten Prozesses besteht darin, Bilder mithilfe spezieller Modelle für maschinelles Lernen zu entrauschen.

Vorwärtsdiffusionsprozess

Der Vorwärtsprozess ist ein fester und nicht erlernbarer Schritt, erfordert jedoch einige vordefinierte Einstellungen. Bevor wir uns mit den Einstellungen befassen, wollen wir zunächst verstehen, wie es funktioniert.

Das Kernkonzept dieses Prozesses besteht darin, mit einem klaren Bild zu beginnen. Bei einer bestimmten Schrittgröße, die mit „T“ bezeichnet wird, wird nach und nach eine kleine Menge Rauschen eingeführt, die einer Gauß-Verteilung folgt.

Wie Sie auf dem Bild sehen können, nimmt das Rauschen mit jedem Schritt zu. Schauen wir uns die mathematische Darstellung dieses Rauschens genauer an.

Rauschen wird aus einer Gaußschen Verteilung abgetastet. Um bei jedem Schritt ein wenig Rauschen einzuführen, verwenden wir eine Markov-Kette. Um ein Bild des aktuellen Zeitstempels zu erstellen, benötigen wir nur ein Bild des letzten Zeitstempels. Das Konzept der Markov-Ketten ist hier von entscheidender Bedeutung und wird für die folgenden mathematischen Details von entscheidender Bedeutung sein.

Eine Markov-Kette ist ein stochastischer Prozess, bei dem die Wahrscheinlichkeit des Übergangs in einen bestimmten Zustand nur vom aktuellen Zustand und der verstrichenen Zeit abhängt, nicht von der vorherigen Abfolge von Ereignissen. Diese Funktion vereinfacht die Modellierung des Rauschadditionsprozesses und erleichtert so die mathematische Analyse.

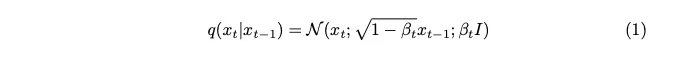
Der als Beta ausgedrückte Varianzparameter ist absichtlich auf einen sehr kleinen Wert eingestellt, um bei jedem Schritt nur ein Minimum an Rauschen einzuführen.

Der Schrittparameter „T“ bestimmt die Schrittgröße, die erforderlich ist, um ein vollständig verrauschtes Bild zu erzeugen. In diesem Artikel ist dieser Parameter auf 1000 festgelegt, was möglicherweise groß erscheint. Müssen wir wirklich 1000 verrauschte Bilder für jedes Originalbild im Datensatz erstellen? Der Aspekt der Markov-Kette hilft nachweislich, dieses Problem zu lösen. Da wir nur das Bild aus dem vorherigen Schritt benötigen, um den nächsten Schritt vorherzusagen, und das bei jedem Schritt hinzugefügte Rauschen gleich bleibt, können wir die Berechnung vereinfachen, indem wir Rauschbilder zu bestimmten Zeitstempeln generieren. Durch den Einsatz einer Paar-Reparametrisierungstechnik können wir die Gleichungen weiter vereinfachen.

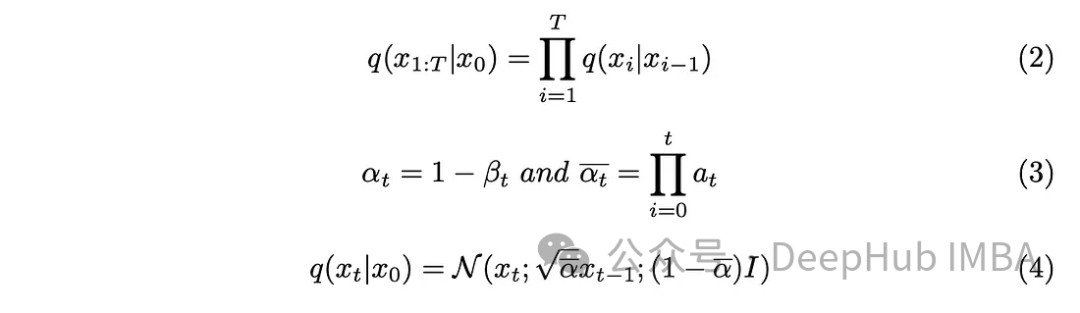
Inkorporieren Sie die in Gleichung (3) eingeführten neuen Parameter in Gleichung (2), entwickeln Sie Gleichung (2) und erhalten Sie das Ergebnis.

Inverser Diffusionsprozess

Wir haben Rauschen in das Bild eingeführt und der nächste Schritt besteht darin, den umgekehrten Vorgang durchzuführen. Sofern wir die Anfangsbedingungen, d. h. das entrauschte Bild bei t = 0, nicht kennen, ist es unmöglich, den umgekehrten Prozess zur Entrauschung des Bildes mathematisch zu implementieren. Unser Ziel ist es, direkt vom Rauschen abzutasten, um neue Bilder zu erstellen, und hier mangelt es an Informationen über die Ergebnisse. Daher muss ich einen Weg finden, ein Bild schrittweise zu entrauschen, ohne das Ergebnis zu kennen. So entstand die Lösung, Deep-Learning-Modelle zu verwenden, um diese komplexe mathematische Funktion zu approximieren.

Mit ein wenig mathematischem Hintergrund nähert sich das Modell Gleichung (5) an. Ein erwähnenswertes Detail ist, dass wir uns an das ursprüngliche DDPM-Papier halten und die Varianz beibehalten, obwohl es auch möglich ist, das Modell dazu zu bringen, sie zu lernen.

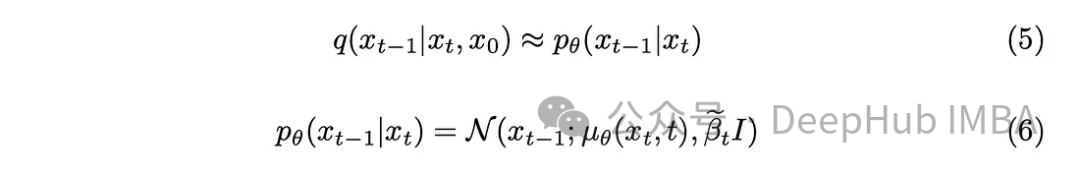
Die Aufgabe des Modells besteht darin, den Durchschnitt des zwischen dem aktuellen Zeitstempel und dem vorherigen Zeitstempel hinzugefügten Rauschens vorherzusagen. Dadurch können Geräusche effektiv entfernt und der gewünschte Effekt erzielt werden. Was aber, wenn unser Ziel darin besteht, dass das Modell das vom „Originalbild“ bis zum letzten Zeitstempel hinzugefügte Rauschen vorhersagen soll? durch Definition der hinteren Varianz.

Die Aufgabe des Modells besteht darin, das dem Bild zum Zeitstempel t hinzugefügte Rauschen aus dem ursprünglichen Bild vorherzusagen. Der Vorwärtsprozess ermöglicht es uns, diesen Vorgang durchzuführen, indem wir mit einem klaren Bild beginnen und zum Zeitstempel t zu einem verrauschten Bild übergehen.

Trainingsalgorithmus

Wir gehen davon aus, dass die Modellarchitektur, die zur Erstellung von Vorhersagen verwendet wird, ein U-Net sein wird. Das Ziel der Trainingsphase besteht darin, für jedes Bild im Datensatz zufällig einen Zeitstempel im Bereich [0, T] auszuwählen und den Vorwärtsdiffusionsprozess zu berechnen. Dadurch entsteht ein klares, etwas verrauschtes Bild, ebenso wie das tatsächlich verwendete Rauschen. Dieses Modell wird dann verwendet, um mithilfe unseres Verständnisses des umgekehrten Prozesses das dem Bild hinzugefügte Rauschen vorherzusagen. Mit realem und vorhergesagtem Rauschen scheinen wir in ein überwachtes maschinelles Lernproblem geraten zu sein.

Die Hauptfrage lautet: Welche Verlustfunktion sollten wir zum Trainieren unseres Modells verwenden? Da es sich um den probabilistischen latenten Raum handelt, ist die Kullback-Leibler-Divergenz (KL) eine geeignete Wahl.

KL-Divergenz misst die Differenz zwischen zwei Wahrscheinlichkeitsverteilungen, in unserem Fall der vom Modell vorhergesagten Verteilung und der erwarteten Verteilung. Die Einbeziehung der KL-Divergenz in die Verlustfunktion führt nicht nur dazu, dass das Modell genaue Vorhersagen liefert, sondern stellt auch sicher, dass die Latentraumdarstellung der gewünschten Wahrscheinlichkeitsstruktur entspricht.

KL-Divergenz kann als L2-Verlustfunktion angenähert werden, sodass die folgende Verlustfunktion erhalten werden kann:

Schließlich erhalten wir den im Artikel vorgeschlagenen Trainingsalgorithmus.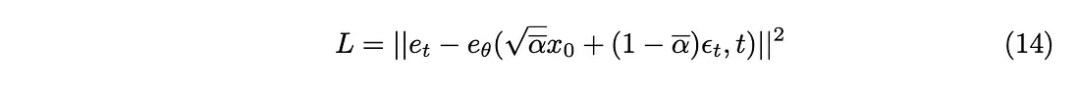

Sampling

Der umgekehrte Vorgang wurde erklärt, hier erfahren Sie, wie Sie ihn verwenden. Ausgehend von einem völlig zufälligen Bild zum Zeitpunkt T und unter Verwendung des umgekehrten Prozesses T-mal erreichen wir schließlich den Zeitpunkt 0. Dies bildet den zweiten in diesem Artikel beschriebenen Algorithmus

Parameter

Wir haben viele verschiedene Parameter Beta, Beta_tildes, Alpha, alpha_hat und so weiter. Ich weiß immer noch nicht, wie ich diese Parameter auswählen soll. Der einzige zu diesem Zeitpunkt bekannte Parameter ist jedoch T, der auf 1000 eingestellt ist.

Bei allen aufgeführten Parametern ist deren Auswahl betaabhängig. In gewisser Weise bestimmt Beta die Menge an Rauschen, die wir bei jedem Schritt hinzufügen möchten. Um den Erfolg des Algorithmus sicherzustellen, ist daher eine sorgfältige Beta-Auswahl von entscheidender Bedeutung. Da es zu viele andere Parameter gibt, lesen Sie bitte das Papier.

Verschiedene Probenahmemethoden wurden während der experimentellen Phase der Originalarbeit untersucht. Die Bilder der ursprünglichen linearen Abtastmethode erhielten entweder zu wenig Rauschen oder waren zu verrauscht. Um dieses Problem zu lösen, wird eine andere, häufigere Methode angewendet, nämlich die Kosinusabtastung. Die Kosinusabtastung sorgt für eine gleichmäßigere und gleichmäßigere Rauschaddition.

Modell-Pytorch-Implementierung

Wir werden die U-Net-Architektur für die Rauschvorhersage verwenden, weil U-Net sich am besten für die Bildverarbeitung und die Erfassung von räumlichen Merkmalen eignet Karten und Bereitstellung und Eingabe einer idealen Architektur für die gleiche Ausgabegröße.

Unter Berücksichtigung der Komplexität der Aufgabe und der Anforderung, für jeden Schritt dasselbe Modell zu verwenden (wobei das Modell in der Lage sein muss, vollständig verrauschte Bilder und leicht verrauschte Bilder mit demselben Gewicht zu entrauschen), wird das Modell optimiert ist ein Muss Unverzichtbar. Dazu gehört das Zusammenführen komplexerer Blöcke und die Sensibilisierung für die verwendeten Zeitstempel über einen sinusförmigen Einbettungsschritt. Der Zweck dieser Verbesserungen besteht darin, das Modell zu einem Experten für Rauschunterdrückungsaufgaben zu machen. Wir werden jeden Block vorstellen, bevor wir mit dem Aufbau des vollständigen Modells fortfahren.

ConvNext Block

Um dem Bedarf nach steigender Modellkomplexität gerecht zu werden, spielt der Faltungsblock eine entscheidende Rolle. Wir können uns hier nicht nur auf die Grundblöcke im U-Net-Papier verlassen, sondern werden sie mit ConvNext kombinieren.

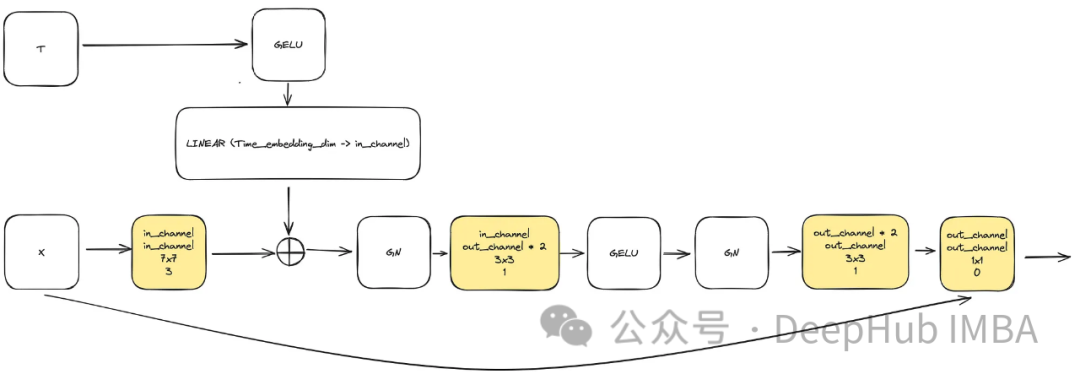
Die Eingabe besteht aus „x“, das das Bild darstellt, und einer eingebetteten Zeitstempelvisualisierung „t“ der Größe „time_embedding_dim“. Während des gesamten Prozesses spielen Blöcke aufgrund ihrer Komplexität und verbleibenden Verbindungen zur Eingabe- und Endschicht eine Schlüsselrolle beim Erlernen von räumlichen Karten und Merkmalskarten.

class ConvNextBlock(nn.Module):def __init__(self,in_channels,out_channels,mult=2,time_embedding_dim=None,norm=True,group=8,):super().__init__()self.mlp = (nn.Sequential(nn.GELU(), nn.Linear(time_embedding_dim, in_channels))if time_embedding_dimelse None) self.in_conv = nn.Conv2d(in_channels, in_channels, 7, padding=3, groups=in_channels) self.block = nn.Sequential(nn.GroupNorm(1, in_channels) if norm else nn.Identity(),nn.Conv2d(in_channels, out_channels * mult, 3, padding=1),nn.GELU(),nn.GroupNorm(1, out_channels * mult),nn.Conv2d(out_channels * mult, out_channels, 3, padding=1),) self.residual_conv = (nn.Conv2d(in_channels, out_channels, 1)if in_channels != out_channelselse nn.Identity()) def forward(self, x, time_embedding=None):h = self.in_conv(x)if self.mlp is not None and time_embedding is not None:assert self.mlp is not None, "MLP is None"h = h + rearrange(self.mlp(time_embedding), "b c -> b c 1 1")h = self.block(h)return h + self.residual_conv(x)

Sinusförmige Zeitstempel-Einbettung

Einer der Schlüsselblöcke im Modell ist der sinusförmige Zeitstempel-Einbettungsblock, der es der Kodierung eines bestimmten Zeitstempels ermöglicht, Informationen über die aktuelle Zeit beizubehalten, die das Modell zum Dekodieren benötigt, weil Das Modell wird für alle verschiedenen Zeitstempel verwendet.

Dis ist eine sehr klassische Implementierung und wird an verschiedenen Stellen angewendet. Das Modul nutzt dies, um eine Zeitdarstellung basierend auf einem gegebenen Zeitstempel t zu erstellen. Die Ausgabe dieses mehrschichtigen Perzeptrons (MLP) dient auch als Eingabe „t“ für alle geänderten ConvNext-Blöcke.

Hier ist „dim“ ein Hyperparameter des Modells, der die Anzahl der für den ersten Block erforderlichen Kanäle angibt. Sie dient als Basisberechnung für die Anzahl der Kanäle in nachfolgenden Blöcken.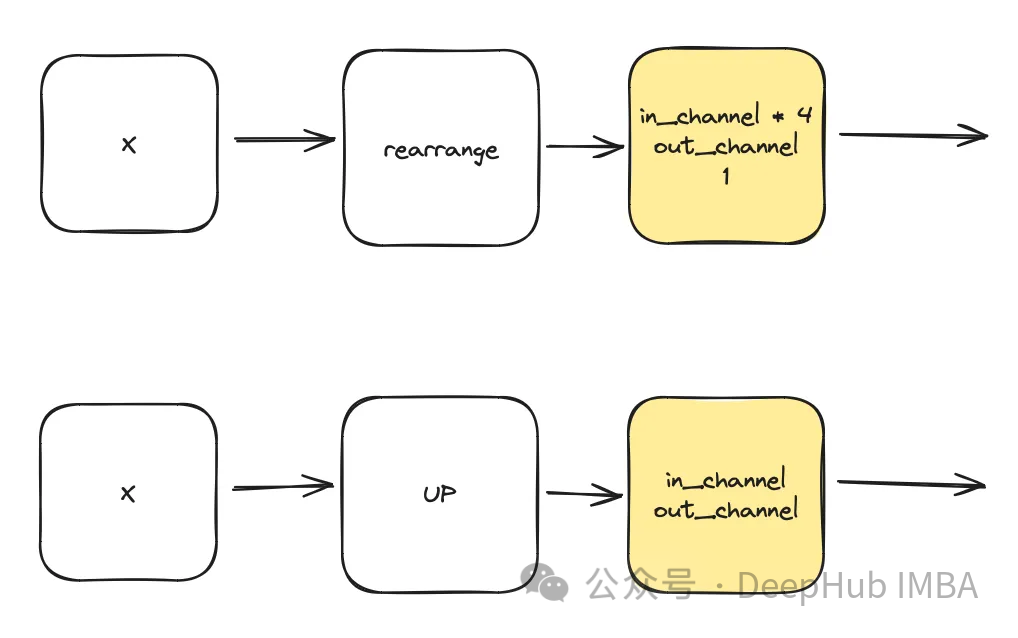

class SinusoidalPosEmb(nn.Module):def __init__(self, dim, theta=10000):super().__init__()self.dim = dimself.theta = theta def forward(self, x):device = x.devicehalf_dim = self.dim // 2emb = math.log(self.theta) / (half_dim - 1)emb = torch.exp(torch.arange(half_dim, device=device) * -emb)emb = x[:, None] * emb[None, :]emb = torch.cat((emb.sin(), emb.cos()), dim=-1)return emb

Achtung

Dies ist eine optionale Komponente, die in unet verwendet wird. Aufmerksamkeit trägt dazu bei, die Rolle verbleibender Verbindungen beim Lernen zu stärken. Es schenkt den wichtigen räumlichen Informationen, die von der linken Seite von Unet erhalten werden, mehr Aufmerksamkeit, indem es den durch Restverbindungen berechneten Aufmerksamkeitsmechanismus und die durch mittlere und niedrige latente Räume berechnete Merkmalskarte verwendet. Es stammt aus dem ACC-UNet-Papier.

gate stellt die hochgetastete Ausgabe des unteren Blocks dar, während x-residual die Restverbindung auf der Ebene darstellt, auf die die Aufmerksamkeit angewendet wird.

class BlockAttention(nn.Module):def __init__(self, gate_in_channel, residual_in_channel, scale_factor):super().__init__()self.gate_conv = nn.Conv2d(gate_in_channel, gate_in_channel, kernel_size=1, stride=1)self.residual_conv = nn.Conv2d(residual_in_channel, gate_in_channel, kernel_size=1, stride=1)self.in_conv = nn.Conv2d(gate_in_channel, 1, kernel_size=1, stride=1)self.relu = nn.ReLU()self.sigmoid = nn.Sigmoid() def forward(self, x: torch.Tensor, g: torch.Tensor) -> torch.Tensor:in_attention = self.relu(self.gate_conv(g) + self.residual_conv(x))in_attention = self.in_conv(in_attention)in_attention = self.sigmoid(in_attention)return in_attention * x

最后整合

将前面讨论的所有块(不包括注意力块)整合到一个Unet中。每个块都包含两个残差连接，而不是一个。这个修改是为了解决潜在的过度拟合问题。

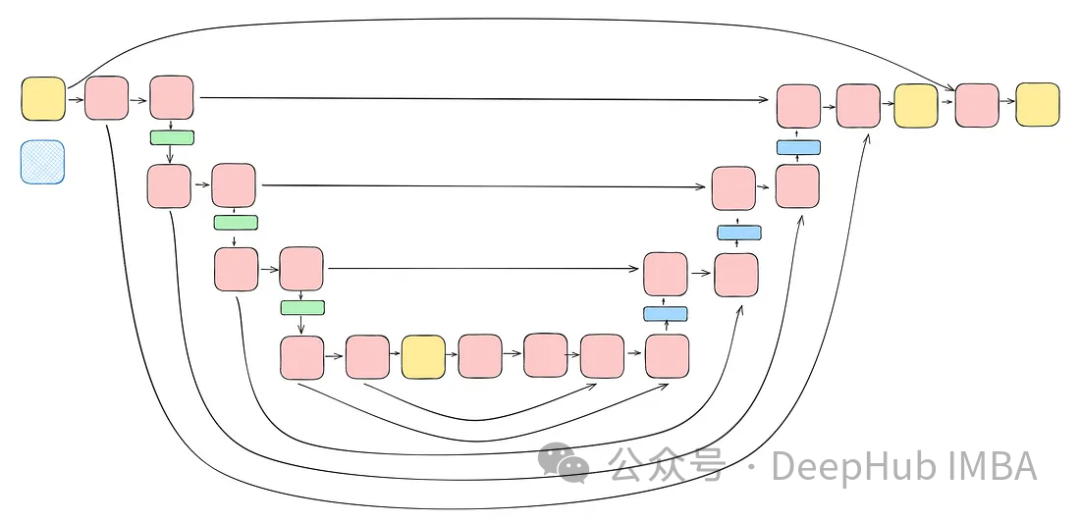
class TwoResUNet(nn.Module):def __init__(self,dim,init_dim=None,out_dim=None,dim_mults=(1, 2, 4, 8),channels=3,sinusoidal_pos_emb_theta=10000,convnext_block_groups=8,):super().__init__()self.channels = channelsinput_channels = channelsself.init_dim = default(init_dim, dim)self.init_conv = nn.Conv2d(input_channels, self.init_dim, 7, padding=3) dims = [self.init_dim, *map(lambda m: dim * m, dim_mults)]in_out = list(zip(dims[:-1], dims[1:])) sinu_pos_emb = SinusoidalPosEmb(dim, theta=sinusoidal_pos_emb_theta) time_dim = dim * 4 self.time_mlp = nn.Sequential(sinu_pos_emb,nn.Linear(dim, time_dim),nn.GELU(),nn.Linear(time_dim, time_dim),) self.downs = nn.ModuleList([])self.ups = nn.ModuleList([])num_resolutions = len(in_out) for ind, (dim_in, dim_out) in enumerate(in_out):is_last = ind >= (num_resolutions - 1) self.downs.append(nn.ModuleList([ConvNextBlock(in_channels=dim_in,out_channels=dim_in,time_embedding_dim=time_dim,group=convnext_block_groups,),ConvNextBlock(in_channels=dim_in,out_channels=dim_in,time_embedding_dim=time_dim,group=convnext_block_groups,),DownSample(dim_in, dim_out)if not is_lastelse nn.Conv2d(dim_in, dim_out, 3, padding=1),])) mid_dim = dims[-1]self.mid_block1 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim)self.mid_block2 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim) for ind, (dim_in, dim_out) in enumerate(reversed(in_out)):is_last = ind == (len(in_out) - 1)is_first = ind == 0 self.ups.append(nn.ModuleList([ConvNextBlock(in_channels=dim_out + dim_in,out_channels=dim_out,time_embedding_dim=time_dim,group=convnext_block_groups,),ConvNextBlock(in_channels=dim_out + dim_in,out_channels=dim_out,time_embedding_dim=time_dim,group=convnext_block_groups,),Upsample(dim_out, dim_in)if not is_lastelse nn.Conv2d(dim_out, dim_in, 3, padding=1)])) default_out_dim = channelsself.out_dim = default(out_dim, default_out_dim) self.final_res_block = ConvNextBlock(dim * 2, dim, time_embedding_dim=time_dim)self.final_conv = nn.Conv2d(dim, self.out_dim, 1) def forward(self, x, time):b, _, h, w = x.shapex = self.init_conv(x)r = x.clone() t = self.time_mlp(time) unet_stack = []for down1, down2, downsample in self.downs:x = down1(x, t)unet_stack.append(x)x = down2(x, t)unet_stack.append(x)x = downsample(x) x = self.mid_block1(x, t)x = self.mid_block2(x, t) for up1, up2, upsample in self.ups:x = torch.cat((x, unet_stack.pop()), dim=1)x = up1(x, t)x = torch.cat((x, unet_stack.pop()), dim=1)x = up2(x, t)x = upsample(x) x = torch.cat((x, r), dim=1)x = self.final_res_block(x, t) return self.final_conv(x)

扩散的代码实现

最后我们介绍一下扩散是如何实现的。由于我们已经介绍了用于正向、逆向和采样过程的所有数学理论，所里这里将重点介绍代码。

class DiffusionModel(nn.Module):SCHEDULER_MAPPING = {"linear": linear_beta_schedule,"cosine": cosine_beta_schedule,"sigmoid": sigmoid_beta_schedule,} def __init__(self,model: nn.Module,image_size: int,*,beta_scheduler: str = "linear",timesteps: int = 1000,schedule_fn_kwargs: dict | None = None,auto_normalize: bool = True,) -> None:super().__init__()self.model = model self.channels = self.model.channelsself.image_size = image_size self.beta_scheduler_fn = self.SCHEDULER_MAPPING.get(beta_scheduler)if self.beta_scheduler_fn is None:raise ValueError(f"unknown beta schedule {beta_scheduler}") if schedule_fn_kwargs is None:schedule_fn_kwargs = {} betas = self.beta_scheduler_fn(timesteps, **schedule_fn_kwargs)alphas = 1.0 - betasalphas_cumprod = torch.cumprod(alphas, dim=0)alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)posterior_variance = (betas * (1.0 - alphas_cumprod_prev) / (1.0 - alphas_cumprod)) register_buffer = lambda name, val: self.register_buffer(name, val.to(torch.float32)) register_buffer("betas", betas)register_buffer("alphas_cumprod", alphas_cumprod)register_buffer("alphas_cumprod_prev", alphas_cumprod_prev)register_buffer("sqrt_recip_alphas", torch.sqrt(1.0 / alphas))register_buffer("sqrt_alphas_cumprod", torch.sqrt(alphas_cumprod))register_buffer("sqrt_one_minus_alphas_cumprod", torch.sqrt(1.0 - alphas_cumprod))register_buffer("posterior_variance", posterior_variance) timesteps, *_ = betas.shapeself.num_timesteps = int(timesteps) self.sampling_timesteps = timesteps self.normalize = normalize_to_neg_one_to_one if auto_normalize else identityself.unnormalize = unnormalize_to_zero_to_one if auto_normalize else identity @torch.inference_mode()def p_sample(self, x: torch.Tensor, timestamp: int) -> torch.Tensor:b, *_, device = *x.shape, x.devicebatched_timestamps = torch.full((b,), timestamp, device=device, dtype=torch.long) preds = self.model(x, batched_timestamps) betas_t = extract(self.betas, batched_timestamps, x.shape)sqrt_recip_alphas_t = extract(self.sqrt_recip_alphas, batched_timestamps, x.shape)sqrt_one_minus_alphas_cumprod_t = extract(self.sqrt_one_minus_alphas_cumprod, batched_timestamps, x.shape) predicted_mean = sqrt_recip_alphas_t * (x - betas_t * preds / sqrt_one_minus_alphas_cumprod_t) if timestamp == 0:return predicted_meanelse:posterior_variance = extract(self.posterior_variance, batched_timestamps, x.shape)noise = torch.randn_like(x)return predicted_mean + torch.sqrt(posterior_variance) * noise @torch.inference_mode()def p_sample_loop(self, shape: tuple, return_all_timesteps: bool = False) -> torch.Tensor:batch, device = shape[0], "mps" img = torch.randn(shape, device=device)# This cause me a RunTimeError on MPS device due to MPS back out of memory# No ideas how to resolve it at this point # imgs = [img] for t in tqdm(reversed(range(0, self.num_timesteps)), total=self.num_timesteps):img = self.p_sample(img, t)# imgs.append(img) ret = img # if not return_all_timesteps else torch.stack(imgs, dim=1) ret = self.unnormalize(ret)return ret def sample(self, batch_size: int = 16, return_all_timesteps: bool = False) -> torch.Tensor:shape = (batch_size, self.channels, self.image_size, self.image_size)return self.p_sample_loop(shape, return_all_timesteps=return_all_timesteps) def q_sample(self, x_start: torch.Tensor, t: int, noise: torch.Tensor = None) -> torch.Tensor:if noise is None:noise = torch.randn_like(x_start) sqrt_alphas_cumprod_t = extract(self.sqrt_alphas_cumprod, t, x_start.shape)sqrt_one_minus_alphas_cumprod_t = extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise def p_loss(self,x_start: torch.Tensor,t: int,noise: torch.Tensor = None,loss_type: str = "l2",) -> torch.Tensor:if noise is None:noise = torch.randn_like(x_start)x_noised = self.q_sample(x_start, t, noise=noise)predicted_noise = self.model(x_noised, t) if loss_type == "l2":loss = F.mse_loss(noise, predicted_noise)elif loss_type == "l1":loss = F.l1_loss(noise, predicted_noise)else:raise ValueError(f"unknown loss type {loss_type}")return loss def forward(self, x: torch.Tensor) -> torch.Tensor:b, c, h, w, device, img_size = *x.shape, x.device, self.image_sizeassert h == w == img_size, f"image size must be {img_size}" timestamp = torch.randint(0, self.num_timesteps, (1,)).long().to(device)x = self.normalize(x)return self.p_loss(x, timestamp)

扩散过程是训练部分的模型。它打开了一个采样接口，允许我们使用已经训练好的模型生成样本。

训练的要点总结

对于训练部分，我们设置了37,000步的训练，每步16个批次。由于GPU内存分配限制，图像大小被限制为128x128。使用指数移动平均(EMA)模型权重每1000步生成样本以平滑采样，并保存模型版本。

在最初的1000步训练中，模型开始捕捉一些特征，但仍然错过了某些区域。在10000步左右，这个模型开始产生有希望的结果，进步变得更加明显。在3万步的最后，结果的质量显著提高，但仍然存在黑色图像。这只是因为模型没有足够的样本种类，真实图像的数据分布并没有完全映射到高斯分布。

有了最终的模型权重，我们可以生成一些图片。尽管由于128x128的尺寸限制，图像质量受到限制，但该模型的表现还是不错的。

注：本文使用的数据集是森林地形的卫星图片，具体获取方式请参考源代码中的ETL部分。

总结

我们已经完整的介绍了有关扩散模型的必要知识，并且使用Pytorch进行了完整的实现，本文的代码：

https://github.com/Camaltra/this-is-not-real-aerial-imagery/

Das obige ist der detaillierte Inhalt vonImplementierung eines Rauschentfernungs-Diffusionsmodells mit PyTorch. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!